Свободные колебания с одной степенью свободы.

Рассмотрим систему материальных точек с одной степенью свободы, подчиненной стационарным связям и находящуюся под действием задаваемых активных сил. Обозначим через q обобщенную координату и предположим, что положение системы, соответствующее нулевому значению координаты , представляет собой положение устойчивого равновесия.

Кинетическая энергия системы , подчиненной стационарным связям, выражается через обобщенные координаты и скорости, а потенциальная энергия является функцией обобщенных координат .

Изучим характер движения системы в области малых значений координаты и обобщенной скорости, т.е. вблизи положения устойчивого равновесия. Примем это положение за начало отсчета обобщенной координаты и за нулевой уровень потенциальной энергии, рассмотрим малые движения системы около положения равновесия. Отклонение системы от положения равновесия будет определяться при таком выборе начальных условий значением обобщенной координаты. Полагая при составлении дифференциальных уравнений малых движений обобщенные координаты и обобщенные скорости малыми величинами, мы ограничимся в дифференциальных уравнениях движения линейными членами. Это прием, заключающийся в отбрасывании в нелинейных дифференциальных уравнениях членов, содержащих квадраты и более высокие степени обобщенных координат и скоростей, называется линеаризацией уравнений. Это позволяет получить замкнутые решения для таких систем, для которой нахождение интегралов точной нелинейной системы уравнений в конечном виде, как правило, невозможно.

Удобным способом составления дифференциальных уравнений малых колебаний является использование уравнений Лагранжа.

Изучим характер движения системы в области малых значений координаты и обобщенной скорости, т.е. вблизи положения устойчивого равновесия.

Кинетическая энергия для системы с одной степенью свободы в обобщенных координатах и обобщенных скоростях имеет вид , где , является положительной функцией обобщенной координаты. Для линеаризации выражения для кинетической энергии разложим в ряд Маклорена вблизи точки :

. Тогда .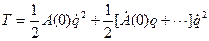

Полагая и малыми величинами, приближенно примем , для краткости обозначим . Эта постоянная положительна, ее называют инерционным коэффициентом. Для линейных обобщенных координат этот коэффициент имеет размерность массы, для угловых координат – размерность момента инерции твердого тела.

Разложим потенциальную энергию также в ряд Маклорена

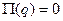, так как положение равновесия выбрано за нулевой уровень потенциальной энергии. Кроме того, в положении равновесия системы равна нулю обобщенная сила, а, следовательно, и первая производная от потенциальной энергии .

Вторая производная от потенциальной энергии в положении устойчивого равновесия удовлетворяет условию . Примем >0 и получим , где с – квазиупругий коэффициент.

Составим уравнения движения Лагранжа или .

В нашем случае , , ,

и уравнение движения будет , a и c - инерционный и квазиупругий коэффициенты.

Введем обозначение и получим 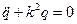. Общий интеграл этого уравнения имеет вид , где амплитуда , и начальная фаза , определяются из начальных условий. Пусть при и ; тогда , . Из формул видно, что амплитуда пропорциональна корню квадратному из полной энергии системы .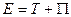

Движение представляет собой гармоническое колебание с частотой и периодом

. Это - свободные и собственные колебания системы.

Частота и период свободных колебаний системы не зависит от начальных условий движения (изохронность малых колебаний) и от природы обобщенной координаты.

Рассмотрим движение в фазовой плоскости. Фазовые траектории можно получить исключением времени из уравнений

и , что приводит к семейству кривых .

К тому же результату придем, написав уравнение семейства уровней полной механической энергии системы . В данном случае консервативной системы фазовые траектории, естественно, совпадают с кривыми уровней энергии.

Для всех эллипсов отношение длин полуосей одно и то же – оно равно частоте собственных колебаний системы.

Покою системы в положении устойчивого равновесия соответствует начало координат фазовой плоскости . При уменьшении полной энергии, а это может иметь место только при уменьшении начальных условий, фазовые траектории стягиваются к началу координат, которое в этом случае называется центром.

Дата добавления: 2015-07-11