
Читайте также:
|
Среди различных методов исследования нелинейных колебаний одним из наиболее распространенных и детально разработанных методов является представление движения на фазовой плоскости. Этот метод позволяет, не интегрируя дифференциальных уравнений, ответить на важные вопросы, характеризующие движение системы. Это существенно, так как во многих случаях нелинейные дифференциальные уравнения не могут быть проинтегрированы в замкнутом виде.
Представление движения на фазовой плоскости позволяет найти возможные состояния равновесия и определить устойчивость равновесия системы.
С помощью построения на фазовой плоскости можно найти периодические движения системы и исследовать переходные процессы к устойчивому состоянию движения в зависимости от различных параметров и начальных условий движения.
В тех случаях, когда нелинейные дифференциальные уравнения могут быть проинтегрированы в замкнутой форме, представление движения на фазовой плоскости позволяет ответить на вопросы об устойчивости возможных состояний равновесия и движения системы и установить влияние различных параметров и начальных условийдвижения и устойчивость этих состояний.
Рассмотрим положения, лежащие в основе исследования движения с помощью фазовой плоскостью дифференциальное уравнение движения при нелинейных колебаниях системы с одной степенью свободы может быть записано в обобщенных координатах в виде
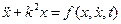 . Обозначив
. Обозначив 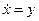 , можно представить это уравнение в виде системы из двух уравнений первого порядка
, можно представить это уравнение в виде системы из двух уравнений первого порядка 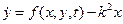 ,
, 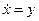 .
.
Ограничиваясь в данном случае рассмотрением автономных систем, запишем систему в виде
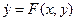 ,
, 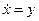 . Плоскость переменных
. Плоскость переменных  и
и 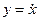 , где
, где  и
и 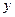 - декартовы прямоугольные координаты, называется фазовой плоскостью. Каждой точке на фазовой плоскости соответствует одно-единственное состояние системы. Поэтому фазовую плоскость иногда называют плоскостью состояний, а точку на фазовой плоскости называют изображающей точкой. Траектория, которую опишет изображающая точка, называется фазовой траекторией.
- декартовы прямоугольные координаты, называется фазовой плоскостью. Каждой точке на фазовой плоскости соответствует одно-единственное состояние системы. Поэтому фазовую плоскость иногда называют плоскостью состояний, а точку на фазовой плоскости называют изображающей точкой. Траектория, которую опишет изображающая точка, называется фазовой траекторией.
Если движение системы периодическое, то фазовая траектория будет замкнутой кривой. Начало координат на фазовой плоскости, где 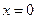 и
и  , является положением равновесия. Дифференциальное уравнение фазовых траекторий
, является положением равновесия. Дифференциальное уравнение фазовых траекторий 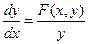 .
.
Через каждую точку фазовой плоскости проходит одна фазовая траектория. Исключением являются точки равновесия, которые называются особыми точками.
Поведение фазовых траекторий вблизи особой точки зависит от параметров системы и от начальных условий системы. Если колебания системы являются периодическими, фазовые траектории в окрестности особой точки являются замкнутыми кривыми. Особая точка в этом случае называется центром.
Колебания механической системы монотонно и неограниченно затухают. Особая точка называется устойчивым фокусом, фазовые траектории - скручивающиеся спирали. Колебания механической системы монотонно и неограниченно возрастают. Особая точка – неустойчивый фокус.
Фазовый портрет системы с особой точкой, называемой седлом. Каждая фазовых кривых пересекает ось только один раз или ни одного раза и, следовательно, движение системы не является колебательным. Кроме криволинейных фазовых траекторий, не пересекающих особую точку, имеются две прямолинейные траектории, проходящие через особую точку, являющиеся асимтотами криволинейных фазовых траекторий.
Фазовые портреты с особыми точками – устойчивым и неустойчивым узлом. Устойчивый узел имеет область притяжения, неустойчивый не имеет области притяжения. Каждая из фазовых траекторий пересекает ось абсцисс только раз, фазовые траектории – не замкнутые кривые, движение не колебательное.
Важное значение при исследовании нелинейных колебаний имеют фазовые траектории, которые, начиная с определенного времени остаются в пределах некоторой конечной области, не приближаясь сколь угодно мало к особой точке. Такие фазовые траектории пересекают бесчисленное число раз ось абсцисс. Возможные формы таких фазовых траекторий – спирали и замкнутые кривые. Замкнутые кривые в этом случае называются предельными циклами. Для скручивающейся спирали предельный цикл лежит внутри спирали, а для раскручивающейся спирали – вне спирали.
Предельные циклы могут быть устойчивыми и неустойчивыми.
Устойчивый предельный цикл характеризуется тем, что при небольших начальных отклонениях от него изображающая точка асимтотически по спирали приближается к предельному циклу. Устойчивому предельному циклу соответствуют автоколебания системы.
Дата добавления: 2015-07-11; просмотров: 107 | Нарушение авторских прав