Истинные приращения функции и аргумента

и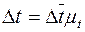

откуда

, .

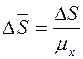Подставим эти значения в равенство (1.7)

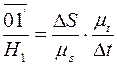, но ;

то есть, V_ср – средняя скорость на первом участке:

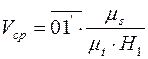. (1.8)

Поскольку величина - представляет собой только масштабы построения, то отрезок , с точностью до постоянного множителя, изображает на диаграмме скороcти (оси V_s) среднюю скорость движения точки С на первом участке. Переносим ее в середину первого участка оси t:

.

Масштабный коэффициент скорости или, сравнивая с (1.8),

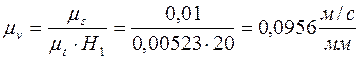. (1.9)

Соединяем точки 1 и 2 хордой на втором участке диаграммы перемещения. Из полюса Р₁ проводим линию Р₁2^’ параллельно хорде 1 2. Отрезок представляет собой среднюю скорость движения на участке 1 2. Полученные точки 1^’, 2^’, 3^’, 4^’, 5^’, 6^’ соединяем плавной кривой. Получим график скорости точки С .

Дата добавления: 2015-07-11