Теоретические основы. 2.1 Уравнение Бернулли для несжимаемой вязкой жидкости в канале

2.1 Уравнение Бернулли для несжимаемой вязкой жидкости в канале

Рассмотрим течение несжимаемой вязкой жидкости в горизонтальном канале, полагая его близким к одномерному, когда v 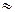w 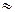0. В этом случае уравнение Навье-Стокса имеет вид:

(2.1)

где = 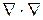- оператор Лапласа; F_x = F_y=0, F_z = -g – проекции массовой силы.

Из последнего уравнения в (2.1) найдем:

. (2.2)

Этот результат позволяет перейти от уравнения Бернулли для струйки тока к аналогичному уравнению, справедливому для всего потока в канале. Для этого произведем осреднение параметров жидкости по расходу в двух сечениях канала:

где Q₁ = Q₂ = Q – объемный расход жидкости; l^(e) – удельная внешняя (по отношению к струйке) работа; l_{тр i} – удельная работа трения, переходящая в теплоту трения (l_{тр i} = q_{тр i}).

С учетом (2.2) полученное уравнение преобразуем к виду:

(2.3)

где u₁, u₂ – среднерасходные скорости ();

- коэффициент Кориолиса ();

l_тех – техническая работа ();

l_тр – работа трения ().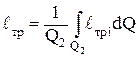

2.2 Ламинарное и турбулентное течения вязкой несжимаемой жидкости в трубе

На рисунке 2.1 изображена картина течения при ламинарном режиме движения жидкости в трубе. В начале трубы имеется ядро с безвихревым течением. Участок течения, где существует ядро, называется начальным (входным, участком гидродинамической стабилизации). Его длина у разных авторов изменяется в пределах: l_н /d = 0,03×Re (по Шиллеру), l_н /d = 0,04×Re (по Таргу), l_н /d = 0,065×Re (по Буссинеску), где Re = ud/n.

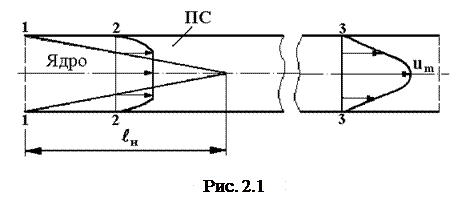Течение в начальном участке может быть рассчитано на основе теории пограничного слоя.

Поле скорости на основном участке находится из решения уравнения Навье-Стокса. В [1], [2] приведено такое решение для трубы эллиптического сечения. С учетом граничного условия уравнение Навье-Стокса преобразуется в уравнение Пуассона:

(2.4)

где u – проекция скорости на ось трубы (v = w = 0); 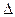p/ l – падение давления на участке длиной 1м; l – длина трубы.

Решение уравнения (2.4) имеет вид [1], [2]:

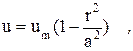
где u_m – скорость на оси трубы; a – длина большой полуоси эллипса; r – текущий радиус.

В частном случае трубы круглого сечения (а = R) распределение скоростей описывается параболой:

, (2.5)

где (2.6)

u_ср – среднерасходная скорость.

В технике потери давления определяют по формуле Дарси-Вейсбаха:

(2.7)

где l - коэффициент гидросопротивления трубы на участке длиной в один калибр.

Выразив Dp через u_ср с помощью (2.6), получим для трубы круглого сечения закон сопротивления Пуазейля:

(2.8)

где .

Подставив (2.8) в (2.7), найдем:

(2.9)

Следовательно, в трубе круглого сечения при ламинарном течении сопротивление движению пропорционально скорости в первой степени. Можно показать, что этот вывод справедлив и для труб плоского и эллиптического сечений [1].

Распределение скорости в трубе характеризуется большой неравномерностью. Коэффициент Кориолиса для ламинарного течения равен a = 2.

При числах Рейнольдса больших критического значения Re_кр=2200 – 2300 в трубе наблюдается турбулентное течение. Длина начального участка значительно короче, чем при ламинарном течении. На рисунке 2.2 изображены начальный и основной участки.

По измерениям Кирстена l_н /d = 50 – 100. Никурадзе получил l_н /d = 25 – 40. В длинных трубах длиной начального участка часто пренебрегают. В коротких трубах потери давления в начальном участке определяют по формуле Вейсбаха:

(2.10)

где x_Н – эмпирический коэффициент сопротивления.

При турбулентном режиме течения отсутствует теоретическое решение уравнений Навье-Стокса. Поэтому при решении практических задач часто поле скорости задают либо полуэмпирическими, либо эмпирическими зависимостями.

Эксперименты показывают, что безразмерные профили скорости в различных сечениях основного участка трубы совпадают друг с другом при их наложении. Поэтому можно записать:

(2.11)

где f (r/R)-функция безразмерного текущего радиуса.

Используя (2.11), найдем расход жидкости:

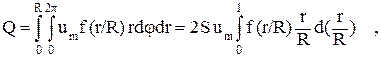(2.12)

где S-площадь сечения трубы.

Видно, что при постоянной площади сечения трубы скорость на оси трубы постоянна, то есть .

Рассмотрим контрольную поверхность радиуса r и длиной l на рисунке 2.3.

При отсутствии массовых сил на жидкость действует сила:

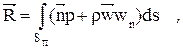
где S_п - площадь проницаемых поверхностей.

Проекция силы на ось х будет равна:

Согласно (2.11) и (2.12) скорости u₁ и u₂ не зависят от координаты х. Поэтому последнее выражение примет вид:

(2.13)

Так как R_x=Пlt, где П - периметр сечения трубы, то из (2,13) найдем:

(2.14)

Используя (2.14), найдем напряжение трения, действующее на жидкость на стенке (при y=0):

. (2.15)

Из (2.14) и (2.15) получим линейный закон изменения касательных напряжений в трубе:

(2.16)

Эта формула справедлива как для турбулентного, так и для ламинарного режима течения (при ламинарном режиме также справедлива формула (2.11)).

2.3 Полуэмпирический логарифмический закон распределения скорости в трубе

Будем полагать, что поток между сечениями 1-1 и 2-2 на рисунке 2.3 состоит из двух слоев и в пределах этих слоев справедливы соотношения:

, ,

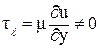(2.17)

, ,

где l - путь смещения.

Рассмотрим течение в ламинарном подслое. Для него при 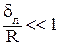уравнение неразрывности имеет вид:

Так как согласно (2.11) и (2.12) , то из него следует v=0. Поэтому проекция на ось х уравнения Навье-Стокса запишется следующим образом:

(2.18)

Дважды интегрируя его, получим:

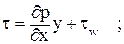
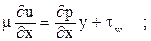
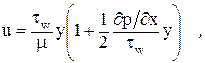
где - напряжение трения на стенке.

При из (2.15) получим или . Подставив найденное значение в предыдущую формулу, получим распределение скорости в ламинарном подслое:

(2.19)

Так как , то приближенно можно записать:

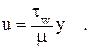(2.20)

Формула (2.20) дает хорошие результаты как для трубы, так и для плоской стенки.

Если ввести условную скорость (скорость трения, динамическую скорость):

(2.21)

то формулу (2.20) можно переписать в виде:

(2.22)

где 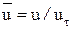- универсальная скорость; - универсальная координата.

Рассмотрим теперь течение жидкости в турбулентном ядре при 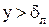.В формуле (2.16) левая часть характеризует отношение напряжений, действующих на верхнерасположенный слой жидкости со стороны нижерасположенного. Используя третий закон Ньютона, из этой формулы получим:

где - напряжение трения, действующее на нижерасположенный слой жидкости со стороны верхнерасположенного.

Используя формулы (2.17) и (2.21), найдем:

Путь смешения определим по формуле А.А. Саткевича [3]:

(2.23)

где - эмпирическая константа.

Подставив (2.23) в предыдущую формулу, получим закон распределения скорости в дифференциальной форме:

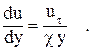
Интегрируя его, найдем логарифмический закон распределения скорости в турбулентной области трубы или плоской стенки:

(2.24)

Для определения константы С_о определим из (2.22) скорость на границе ламинарного подслоя:

(2.25)

Используя это значение, из (2.24) найдем:

Тогда (2.24) можно переписать в виде:

(2.26)

где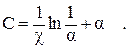

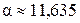Согласно эксперименту . Подставив , получим С =5,5, справедливое для гладких стенок. В этом случае формула (2.26) примет вид:

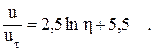(2.27)

Толщина вязкого подслоя равна:

Следовательно, формула (2.27) применима при . На практике ее применяют обычно при вплоть до оси трубы. Закон (2.27) хорошо подтверждается опытом в широком диапазоне изменения числа Re.

Опыты показывают, что чисто ламинарное течение в ламинарном подслое наблюдаются при , то есть при . Тем не менее, в расчетах часто пользуются формулой .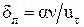

Число Re, составленное для ламинарного подслоя, имеет значение:

(2.28)

Видно, что с увеличением скорости потока величина уменьшается.

Используя (2.27), можно найти максимальную и среднерасходную скорости:

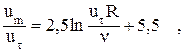
(2.30)

Дата добавления: 2015-07-10