Читайте также:
|
Из (2.29) и (2.30), исключив скорость на оси трубы, получим:
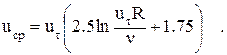(2.35)
Из формулы (2.15) определим перепад давления:
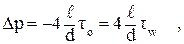(2.36)
где d = 2 R.
Исключив с помощью (2.36) величину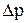 
в формуле (2.7), найдем коэффициент гидросопротивления:
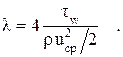(2.37)
Используя (2.21), исключим величину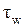 
. После преобразований получим:
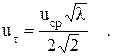(2.38)
Величину, входящую под знак логарифма в (2.35), преобразуем к виду:
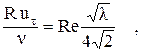(2.39)
где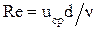 
.
Подставив (2.38) в (2.35) и учтя (2.39), получим универсальный закон сопротивления:
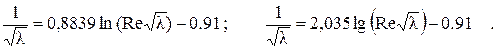(2.40)
Для лучшего совпадения с опытом Никурадзе несколько изменил коэффициенты в (2.40):
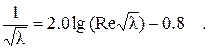(2.41)
В литературе эту формулу называют формулой Никурадзе-Прандтля для гладких труб. В явном виде закон сопротивления записывается с помощью аппроксимации:
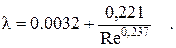(2.42)
При числах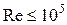 
часто пользуются формулой Блазиуса, полученной эмпирическим путём:
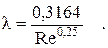(2.43)
Формула П.К. Конакова справедлива в широком диапазоне чисел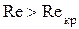 
, так как она является аппроксимацией универсального закона сопротивления в явном виде:
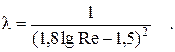(2.44)
Дата добавления: 2015-07-10; просмотров: 260 | Нарушение авторских прав