Течение жидкости в шероховатых трубах

Все технические трубы имеют шероховатые стенки. Техническая шероховатость имеет самые различные размеры, геометрические формы и распределение по поверхности. Это чрезвычайно сильно затрудняет её количественную оценку и её влияние на движение жидкости. Для более простой оценки шероховатости вводят понятие песочной или эквивалентной шероховатости, под которой понимают такую высоту выступов песчинок 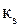, которая создаёт сопротивление, равное действительному сопротивлению данного трубопровода.

Влияние песочной шероховатости подробно изучено И.И. Никурадзе. Он оклеивал стенки труб песком с зернами определённого размера, расположенными очень плотно. Путем выбора различных диаметров труб и различных зерен песка, параметр , где R-радиус трубы, варьировался в диапазоне 1/500 – 1/15. Характер поведения кривых коэффициента сопротивления показан на рисунке 2.4.

При ламинарном течении все шероховатые трубы имеют такое же сопротивление, что и гладкие. Это объясняется тем, что вязкая жидкость заполняет впадины между бугорками и ламинарность течения не нарушается. Критическое число 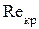и сопротивление в переходной области также практически не зависят от шероховатости.

При турбулентном режиме течения следует различать три режима:

· режим без проявления шероховатости, при котором:

Размеры зерен столь малы, что все выступы элементов шероховатости лежат внутри ламинарного подслоя . Такие трубы называются гидравлически гладкими;

· переходный режим, при котором:

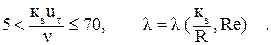
Этот режим наступает при увеличении числа Re и уменьшении при этом толщины ламинарного подслоя , когда гребешки шероховатости частично попадают в область турбулентного течения 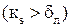, вызывая дополнительные завихрения и потери энергии;

· режим с полным проявлением шероховатости, при котором:

Все элементы шероховатости выступают из ламинарного подслоя 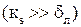. Сопротивление обусловлено в основном сопротивлением формы отдельных элементов шероховатости. Этот режим часто называют еще автомодельным относительно числа Re и режимом квадратичной зависимости гидросопротивления от скорости .

Для определения коэффициента гидросопротивления шероховатых труб получена интерполяционная формула:

(2.45)

При 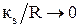она переходит в формулу(2.41). При 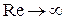- в формулу Никурадзе для шероховатых труб:

(2.46)

Очень часто пользуются формулой Шифринсона:

(2.47)

Для всех турбулентных режимов Альтшуль предложил приближенную формулу:

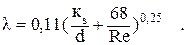(2.48)

При она практически совпадает с формулой (2.43), а при 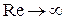- с формулой (2.47).

Как уже отмечалось, расчет труб с технической шероховатостью производят с помощью формул, в которых используется понятие эквивалентной шероховатости. Если, например, подставить опытное значение в формулу (2.46), то для трубы с технической шероховатостью можно найти соответствующее значение эквивалентной шероховатости. Значения 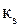для технических труб приведены в справочниках по гидравлическим сопротивлениям.

Следует отметить, что в технически шероховатых трубах переход от режима без проявления шероховатости при малых числах Re к режиму с полным проявлением шероховатости при больших числах Re происходит более постепенно, чем в трубах с песочной шероховатостью.

2.7 Гидравлическое сопротивление труб с некруглым поперечным сечением

Для приближённой оценки сопротивления трубы некруглого сечения применяют приём, основанный на сопоставлении сопротивления этой трубы с эквивалентной ей по сопротивлению трубой круглого сечения. За диаметр у трубы некруглого сечения принимается гидравлический диаметр:

(2.49)

где s – площадь поперечного сечения;

П – смоченный периметр.

В некоторых случаях используется гидравлический радиус .

Формула (2.49) обеспечивает учёт влияния формы сечения и смачиваемого периметра на режим течения и сопротивление труб некруглого сечения. Опыты показывают, что для расчёта сопротивления труб некруглого сечения применимы все формулы для круглых труб, если в них диаметр заменить на гидравлический диаметр.

Следует заметить, что данный приём очень грубый и имеет смысл только, если у сравниваемых труб сечения геометрически близки друг к другу [1].

2.8 Гидравлические потери – потери трения и местные потери

Источником гидравлических потерь при движении реальной жидкости является процесс необратимого перехода механической энергии потока в теплоту (диссипативный процесс). Этот переход энергии обусловлен молекулярной и турбулентной вязкостью жидкости.

Различают два вида потерь – потери трения и местные потери.

Потери трения вызываются вязкостью жидкости и являются результатом обмена количеством движения между молекулами и молями соседних слоёв жидкости, движущихся с различными скоростями. Эти потери имеют место на протяжении всей длины трубопровода. Поэтому их часто называют также потерями по длине.

Местные потери возникают при местном нарушении нормального течения потока, при отрыве его от стенки и вихреобразовании в местах изменения конфигурации трубопровода или встречи препятствий.

Все виды потерь происходят на участке трубопровода определённой длины. Местные потери неотделимы от потерь на трение. Для удобства расчёта их условно считают сосредоточенными в одном сечении и не включающими потери на трение. Суммирование же потерь производится по принципу наложения потерь, при котором берётся арифметическая сумма потерь на трение и местных потерь.

Гидравлические потери на участке канала могут быть рассчитаны с помощью уравнения Бернулли, записанного в одном из следующих видов:

(2.50)

где - потенциальная энергия положения жидкости, отсчитанная от произвольной нивелирной плоскости, или геометрический напор;

- потенциальная энергия давления жидкости или пьезометрический напор;

- кинетическая энергия жидкости или скоростной напор.

Левая часть во втором уравнении (2.50) характеризует полный напор жидкости, обычно обозначаемый через

(2.51)

Общепринято гидравлические потери выражать в паскалях или в метрах столба жидкости, что соответствует методике их экспериментального измерения:

(2.52)

Для случая, когда , эти уравнения примут вид:

При они ещё больше упростятся:

где

- осреднённое полное давление;

- коэффициент Кориолиса.

При равенстве площадей канала из уравнения расхода следует равенство скоростей . В этом случае будем иметь:

где для развитого течения .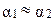

Уравнение Бернулли, как правило, используется для определения падения полного давления на участке канала 1 – 2 и для определения потребной величины для обеспечения заданного полного давления . Для этого необходимо знать величину гидравлических потерь , то есть рассчитывать их без использования уравнения Бернулли.

Для оценки гидравлических потерь вводят коэффициент гидросопротивлений как отношение потерянной удельной энергии к кинетической энергии в принятом сечении:

(2.53)

Формула (2.53) называется формулой Вейсбаха. Из неё следует, что величина зависит от положения сечения, к которому она приведена. Пересчёт коэффициента в зависимости от положения сечения можно выполнить по формуле:

(2.54)

Для трубопроводов коэффициент трения всего рассчитываемого элемента удобнее выразить через коэффициент сопротивления трения единицы относительной длины участка, то есть:

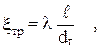(2.55)

где - гидравлический диаметр.

Потери давления определятся тогда по формуле Дарси – Вейсбаха:

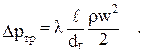(2.56)

Величины коэффициентов гидросопротивления в общем случае зависят от следующих параметров:

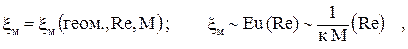
где Eu, M – числа Эйлера и Маха.

Дата добавления: 2015-07-10