|
Читайте также: |
Таким образом, ОПФ в математическом выражении представляет собой преобразование Фурье функции рассеяния А(х', у') оптической системы:
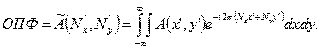(6.8)
Выражая функцию (6.4) через модуль и аргумент, получим
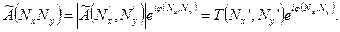(6.9)
Модуль оптической передаточной функции Т(Nx, Ny) показывает зависимость изменения амплитуды функции распределения освещенности в изображении от пространственной частоты, а изменение амплитуды в плоскости изображения пропорционально коэффициенту передачи контраста. Коэффициентом передачи контраста TN называют отношение контраста изображения к контрасту предмета (TN = Kи/Kп). Контраст для синусоидального предмета и его изображения определяют по формуле
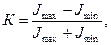(6.10)
где Jmax и Jmin – максимальная и минимальная интенсивности света (яркость для плоскости предмета Lmax, Lmin; освещенность в плоскости изображения Еmах, Еmin).
Модуль оптической передаточной функции называют частотно-контрастной
характеристикой (ЧКХ), так как она показывает зависимость коэффициента передачи контраста от пространственной частоты, или пространственно-частотной характеристикой (ПЧХ), так как она рассматривается в двумерном пространстве, а также модуляционной передаточной функцией (МПФ) или функцией передачи модуляции (ФПМ) по аналогии с передачей электрических сигналов. Так как формула контраста (6.5) для синусоидального объекта аналогична формуле модуляции для электрических сигналов, коэффициент передачи контраста называют коэффициентом передачи модуляции (КПМ). Тогда ФПМ определяется как зависимость коэффициента передачи модуляции от пространственной частоты.
Аргумент передаточной функции φ(N'x, N'у) показывает зависимость фазы от пространственной частоты. Эту зависимость называют частотно-фазовой характеристикой или функцией передачи фазы (ФПФ).
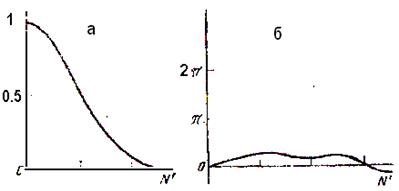
Графические представления ФПМ и ФПФ для типового случая (рисунок 6.6) показаны для одного направления в плоскости изображения, т. е. в направлении сканирования изображения. ФПМ (рисунок 6.9, а) нормируется для нулевой пространственной частоты. При N = 0 ФПМ имеет максимальное значение, равное 1. Значение ФПФ (рисунок 6.9, б) при N = 0 равно нулю. Максимальное значение изменения фазы равно 2л. Наличие ФПФ определяется несимметричностью функции рассеяния оптической системы, это указывает на несимметричные остаточные аберрации (кому). Если функция рассеяния симметрична, то нетрудно показать, используя формулу (6.4), что ФПФ при этом отсутствует и оптическая передаточная функция определится только ФПМ. Оптические системы высокого качества имеют незначительные фазовые изменения, поэтому, как правило, исследование проводят только по ФПМ, которая дает наиболее полную объективную информацию об оптической системе.
Числовые критерии по ФПМ разрабатывают для оптических систем каждого типа. Например, для систем кинематографии предложена «критическая» пространственная частота, при которой коэффициент передачи модуляции уменьшается в е раз, т. е. при Т = 0,368; для фотографических систем используют среднюю пространственную частоту в сюжетно важном интервале пространственных частот. Для малоформатных объективов, снимки от которых рассматривают визуально с расстояния наилучшего видения, этот интервал находится в пределах 0 – 40 мм-1. Значения допустимых коэффициентов передачи модуляции при заданных частотах могут быть получены на стадии расчета оптических систем и, следовательно, установлены технические условия на реальные объективы, согласно которым осуществляется выбор числовых критериев оценки качества изображения
6.5. Разрешающая способность оптической системы
6.5.1 Предельная разрешающая способность по Релею
Разрешающая способность определяет способность оптической системы изображать раздельно два близко расположенных точечных предмета.
Предельная разрешающая способность – это минимальное расстояние sR между двумя точками, при котором их изображение отличимо от изображения одной точки.
Критерий Релея гласит, что при провале в распределении интенсивности в изображении двух близких точек в 20% точки будут восприниматься как раздельные. Для этого необходимо, чтобы центральный максимум в изображении одной точки приходился бы на первый минимум в изображении другой (рис. 6.10).
Для оптических систем при отсутствии аберраций канонических единиц. Разрешение по Релею удовлетворительно характеризует качество изображения астрономических телескопов, спектральных приборов, для которых предметами являются близко расположенные точки или линии, а также визуальных приборов (предназначенных для работы с глазом).
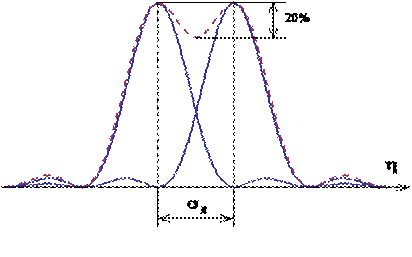. Рис.6.10 Разрешение по Релею. (ρ0)
6.5.2. Разрешающая способность по Фуко
Критерий Фуко применяется для оценки качества изображения оптических систем, передающих объекты сложной структуры. Разрешающая способность R определяется как максимальная пространственная частота периодического тест-объекта, состоящего из черно-белых штрихов (миры Фуко), в изображении которого еще различимы штрихи. Разрешающую способность обычно определяют для миры единичного (абсолютного) контраста по графику ЧКХ оптической системы (рис. 6.11.). Разрешающая способность R определяется для заданного контраста (обычно для контраста k =0.2).
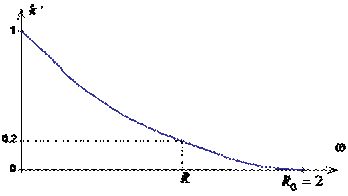
Рис.6.11 Разрешающая способность по Фуко
Предельная разрешающая способность R0 для оптических систем определяется размерами зрачка, длиной волны и аберрациями.
Числовым критерием оценки качества изображения по ФПМ является и разрешающая способность, так как она представляет собой предельную пространственную частоту при минимальном коэффициенте передачи контраста. В качестве критерия качества изображения оптических систем разрешающую способность стали использовать с момента появлении относительно сложных оптических приборов – телескопов. Этот критерий был предложен Рэлеем как обратная величина наименьшего расстояния между двумя различаемыми светящимися точками или линиями. Наименьшее разрешаемое расстояние ρ0 для безаберрационной оптической системы равно радиусу центрального кружка дифракционной картины изображения бесконечно удаленной светящейся точки или расстоянию между максимумами функций рассеяния двух светящихся точек, когда максимум одной функции рассеяния совпадает с первым минимумом другой (рисунок 6.10). Это расстояние ρ0 = 1,22λ f ’/D, где λ – длина волны света; f ' и D – соответственно фокусное расстояние и диаметрвходного зрачка объектива.
Разрешающая способность для одного направления функции рассеяния
N0 = 1/ρ. Разрешающая способность определена по критерию Рэлея из предположения визуального наблюдения для точки изображения, расположенной на оптической оси. Разрешающая способность Nф объектива и фотографического слоя (фотографическая разрешающая способность) может быть найдена по эмпирической формуле:
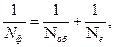(6.11)
где No6 – визуальная разрешающая способность объектива; Ne – разрешающая способность фотослоя.
Оценка качества изображения оптических систем, используемых в приборах для воспроизведения визуального изображения, по числовым критериям не дает полного представления о их передающих свойствах и применяется в основном для контроля годности продукции. По виду кривой ФПМ, дающей наиболее полную информацию о качестве изображения в рабочем диапазоне пространственных частот, проводят исследования оптических систем на стадии разработки.
6.5.3 ФРТ идеального телескопа
Форма изображения точечного источника (звезды) в идеальном телескопе без атмосферы определяется только дифракцией и описывается функцией 
Эйри:
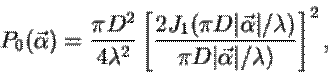
(6.12)
Рис.6.12. Функция рассеяния идеального телескопа
где:
; 
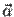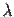- длина волны света;
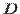- диаметр апертуры телескопа;
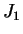- так называемая функция Бесселя.
Первое темное кольцо находится на угловом расстоянии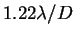 
от центра. Часто это расстояние считается мерой разрешения идеального телескопа.
Изображение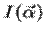 
астрономического объекта 
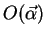можно рассматривать как множество изображений точек, каждое из которых описывается функцией Эйри. Это можно записать как свертку:
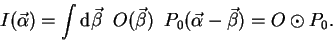(8.13)
Ее называют уравнением изображения. По сравнению с объектом изображение более сглаженное, разрешение уменьшается. Однако, для заданного диаметра телескопа 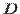это ухудшение - наименьшее возможное. В этом случае говорят, что разрешение в изображении ограничено ифракцией.
6.5.4 Влияние аберраций на ОПФ.
При наличии аберраций ОПФ оптической системы становится меньше, чем ОПФ безаберрационной системы. На графике ЧКХ можно показать, как аберрации влияют на форму кривой контраста (рис.6.13.). Кривые ЧКХ в присутствии аберраций могут иметь сложную форму, но они никогда не превышают кривую безаберрационной ЧКХ.
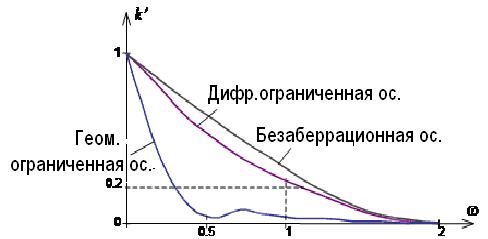
Рис.6.13. Влияние аберраций на ЧКХ.
Дифракционно-ограниченные оптические системы имеют рабочий интервал частот, превышающий половину от предельной, то есть w>1 (рис.6.13). Качество изображения в таких системах определяется в основном явлениями дифракции и непосредственно зависит от отношения апертуры к длине волны A/l. Остаточные аберрации должны оцениваться по критерию Марешаля. К дифракционно-ограниченным системам относятся, в частности, измерительные системы, проекционные оптические системы для микроэлектроники и системы, работающие с глазом.
К геометрически-ограниченным относятся оптические системы, рабочий интервал частот для которых не превосходит w=0.5 в канонических частотах (рис. 6.13). Качество изображения таких систем определяется картиной поперечных аберраций и непосредственно не зависит от длины волны и апертуры. Степень коррекции геометрически-ограниченных систем оценивается поперечными аберрациями. К таким системам относятся, в частности, кино-, фото- и телевизионные объективы.
6.6 Измерение остаточных аберраций
Измерение остаточных аберраций корригированных оптических систем (фотографических объективов, объективов зрительных труб, элементов оборачивающих систем и др.) выполняют в целях выявления соответствия реальных аберраций их теоретическим значениям, на основании чего судят о возможности использования контролируемого объектива по прямому назначению. Так, если измеренная дисторсия аэрофотосъемочного объектива окажется большой, то объектив нельзя использовать для точных топографических работ, например составления карты местности. В этом случае необходимо выявить возможные нарушения технологического процесса изготовления объектива или другие причины несоответствия измеренных аберраций допустимым значениям.
6.6.1 Измерение сферической аберрации объективов
Сферическая аберрация может быть измерена методом, основанным на определении координат точек пересечения с задней фокальной плоскостью лучей, прошедших через отдельные зоны контролируемого объектива (рисунок 6.14, а). Он позволяет измерить продольную и поперечную сферическую аберрацию объектива и его вторичный спектр
Прямоугольная щель 3 установлена в заднем фокусе F'к объектива 4 коллиматора и освещается источником света 1 через конденсор 2 и сменный светофильтр С. За объективом 4 установлены две щелевые диафрагмы 5, представляющие собой два прямоугольных отверстия в непрозрачном экране. Принято выбирать ширину b каждого отверстия равной 1/100 фокусного расстояния контролируемого объектива; высоту h = 3b и расстояние между отверстиями d = 2b. Диафрагмы 5 устанавливают на подвижные каретки так, чтобы длинная сторона каждой щели была параллельна длинной стороне щели 3. Диафрагмы 5 называют также подвижными диафрагмами. За исследуемым объективом 6 на отсчетной каретке устанавливают микроскоп М, который содержит объектив 7 и сетку 8. Окуляром 9 микроскопа, как правило, служит окуляр-микрометр.
Диафрагма 5 выделяет из параллельного пучка лучей, идущих из коллиматора, узкий пучок в зоне m. В фокальной плоскости объектива 6 формируется дифракционное изображение щели 3, представляющее собой характерную картину, так называемый «тройник» (рисунок 6.14, б), состоящий из трех линий (на рисунке изображены темными), расположенных параллельно длинным сторонам щелевых диафрагм 3 и 5. Если диафрагму 5 перемещать перпендикулярно к оптической оси, т. е. открывать различные зоны т объектива, то при отсутствии сферической аберрации тройник будет неподвижным, в противном случае смещение тройника зависит от положения диафрагмы 5, т. е. от значения m. Предметная точка микроскопа М совмещена с задним фокусом F' объектива 6.
При измерении поперечной сферической аберрации Δy' используется только одна диафрагма 5, а значение ℓ смещения тройника измеряется с помощью окуляра-микрометра путем наведения перекрестия на центральную светлую линию тройника. Очевидно что ℓ = Δy'β, где β – линейное увеличение микрообъектива 7. Так как значение β входит в результаты измерения, его следует измерить заранее; в лабораторной практике используют аттестованный микрообъектив, линейное увеличение которого измерено с высокой точностью. В результате измерений значения ℓ для нескольких зон объектива получают зависимость ℓ = ℓ(m) в виде табличных данных, с помощью которых строят кривую поперечной сферической аберрации в общепринятом виде: Δy'= f (tgσ’), где tgσ’ = m/ f ’ (f ’ – фокусное расстояние контролируемого объектива).
Наиболее ответственной операцией при измерении поперечной сферической аберрации является наведение нити окуляра-микрометра на середину светлой линии тройника, который представляет собой дифракционное изображение щели 3, построенное двумя отверстиями шириной b с расстоянием между ними d = 2b. В этом случае расстояние от центра главного максимума нулевого порядка до первого минимума определяется в угловой мере выражением sinφ = λ/(2d), где λ – длина волны света. Если b = 0,01 f ’, то sinφ = 25λ. Линейное расстояние от центра изображения до первого минимума f sin ф = 25λ, а ширина всего изображения равна 50λ, или 0,025 мм.
Если принять, что визуально изображение можно разделить нитью на две равные части с погрешностью до 1/5 его ширины, то погрешность наведения составит 0,005 мм. Это и есть главная погрешность при измерении поперечной сферической аберрации. С учетом других погрешностей на практике принято считать, что суммарная погрешность измерения поперечной аберрации составляет 0,01 – 0,015 мм независимо от значения самой аберрации. При измерении продольной сферической аберрации используют обе диафрагмы 5, устанавливая их на симметричных зонах относительно оси объектива 6. При наличии сферической аберрации в поле изображения микроскопа видны два тройника (рис. 6.14, в). Микроскоп М перемещают вдоль оси до тех пор, пока оба тройника не сольются в один. Очевидно, что в этом случае предметная плоскость микроскопа проходит через точку пересечения лучей (точнее – узких пучков лучей), идущих через зоны т контролируемого объектива. Если в первоначальном положении микроскопа его предметная плоскость была совмещена с параксиальным фокусом объектива, то значение перемещения микроскопа для различных зон есть не что иное, как продольная сферическая аберрация объектива.
Началом отсчета положения микроскопа не обязательно должна быть именно задняя фокальная плоскость, проходящая через параксиальный фокус объектива. При обработке результатов измерения сравнительно просто строят кривую продольной (или поперечной) сферической аберрации для любой другой плоскости установки известными приемами.
6.6.2. Измерение дисторсии объективов
Дисто́рсия— аберрация оптических систем, при которой линейное увеличение изменяется по полю зрения. При этом нарушается подобие между объектом и его изображением.Исправляется подбором линз и других элементов оптической системы при её разработке. Если присутствует в цифровом изображении, может быть исправлена программно.
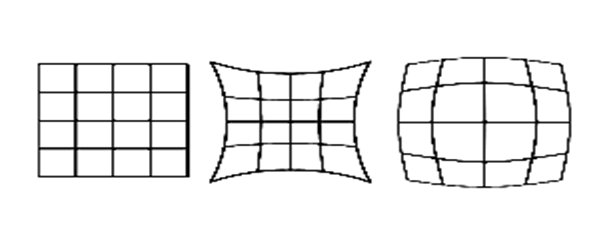Рис.6.15. Изображение идеальное без дисторсии, с «подушкой» и «бочкой».
Изображение квадрата, получаемого объективом с дисторсией, имеет вид подушки (подушкообразная дисторсия, подушка) при положительной дисторсии, и вид бочки (бочкообразная дисторсия, бочка) при отрицательной (см. рис.6.15.). В отдельных случаях искажения формы могут иметь и более сложный вид. От диафрагмирования апертурной или виньетирующей диафрагмой дисторсия не зависит, поскольку таким способом невозможно изменить увеличение.
Количественно дисторсия может быть выражена через так называемую относительную дисторсию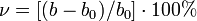 
, где b 0 — линейное увеличение идеальной системы без дисторсии, b — реальное увеличение. На оптической оси увеличение равно идеальному, отклонение от него обычно достигает максимума по краю поля зрения. Поэтому для характеристики дисторсии оптической системы обычно за b берётся увеличение по краю.Для одной и той же системы дисторсия зависит от расстояния до объекта, и, соответственно, от увеличения b 0. Как правило, если дисторсия мала или отсутствует при одном расстоянии, она будет мала и при другом.Дисторсия зависит также и от длины волны, что даёт побочный эффект, сходный с хроматизмом увеличения, и может считаться хроматической аберрацией. Поэтому, строго говоря, дисторсия снижает разрешающую способность, хотя влияние этого обычно невелико.
В зрительных трубах и биноклях дисторсия может быть уничтожена практически полностью.
Дверные глазки, которые представляют собой широкоугольные зрительные трубы, намеренно изготавливаются с очень большой бочкообразной дисторсией, чтобы можно было, сохраняя широкий угол зрения, рассмотреть при большом увеличении лицо по центру.
Для объективов, близких к симметричным, дисторсия обычно очень мала, даже если линейное увеличение не равно -1, что имеет место в подавляющем большинстве реальных случаев.
Характерная величина относительной дисторсии нормального объектива 0,5 %. В целом, у длиннофокусных объективов дисторсия меньше, чем у нормальных, у широкоугольных — больше.Объективы с исправленной дисторсией называются ортоскопическим.
В некоторых случаях к исправлению дисторсии предъявляются повышенные требования. Так, в объективах для аэрофотосъемки относительная дисторсия составляет порядка 0,01 %.Иногда, напротив, величина дисторсии не важна. Объективы с неисправленной дисторсией называются дисторзирующими, они применяются, например, для метеорологических наблюдений.
Определение дисторсии съемочных объективов основано на измерении поперечного смещения изображения предмета при повороте объектива вокруг его задней узловой точки.
У объективов, рассчитанных для работы с конечного расстояния, определение дисторсии основано на измерении величины изображения шкалы, установленной в предметной плоскости, и сравнении этой величины с рассчитанной по формулам параксиальной оптики.
Для проверки расчетного значения дисторсии ее необходимо определять при диафрагмировании объектива до значении 1:8— 1:10.
Дисторсию с учетом влияния других аберраций объектива необходимо определять при полном относительном отверстии объектива.
Измерение дисторсии съемочных объективов должно производиться на оптической скамье по схеме Рис 6.16, а для объективов, рассчитанных для работы с конечного расстояния, — по схеме Рис.6.17.
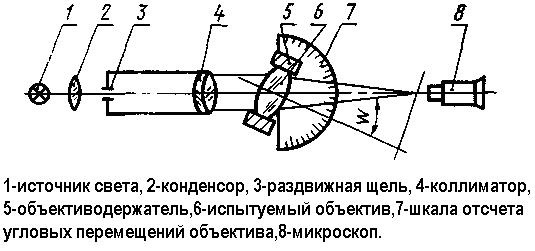
Рис. 6.16. Оптическая схема установки для измерения дисторсии.
Световой диаметр коллиматора при измерении дисторсии должен превышать диаметр входного зрачка испытуемого объектива на 10—20%.
Объективодержатель (5) Рис.6.16 должен иметь возможность перемещения в горизонтальной плоскости вдоль оптической оси коллиматора и перпендикулярно к ней, а также вращения вокруг вертикальной оси для совмещения с ней задней узловой точки объектива. Радиальное биение при вращении объективодержателя вокруг вертикальной оси не должно превышать 0,005 мм.
Микроскоп должен иметь окулярный микрометр и механизм микрометренного перемещения вдоль оптической оси
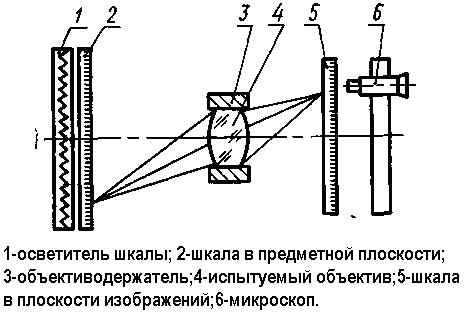
Рис.6.17. Оптическая схема для измерения дисторсии у объективов предназначенных для съемки на конечных расстояниях.
.Апертура микрообъектива микроскопа (Рис.6.17) должна быть больше апертуры испытуемого объектива в пространстве изображений. Увеличение микроскопа должно быть 80—100х.
Шкала в предметной плоскости объектива должна иметь
светлые штрихи на темном фоне, шкала в плоскости изображений — темные штрихи на светлом (прозрачном) фоне.
Количество равноотстоящих друг от друга штрихов на каждой шкале должно быть таким, чтобы в поле зрения объектива умещалось 10—20 штрихов (по 5—10 штрихов на каждом радиусе поля зрения, не считая нулевого штриха).
.Измерение дисторсии проводится путем измерения для каждого значения W (- W) a1= aw1- a-w1. Для каждого значения ai определяют дисторсию по формуле:
Qy1w= n ai 2cosW, (6.14)
Где n - цена деления окулярного микроскопа с учетом увеличения микроскопа (мм).
Wi - угол заклона объектива (град.)
ai - значение дискрета сетки (мм)
После измерений строят график дисторсии. Для этого по оси абцисс откладывают значения дисторсии, а по оси ординат откладывают величину линейного поля зрения испытуемого объектива в мм.
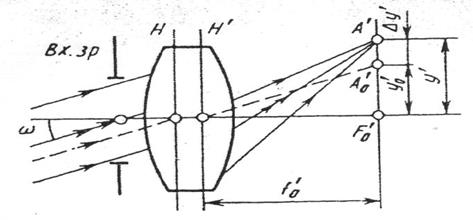
Рис.6.17а Ход лучей в объективе при дисторсии
Дисторсию объектива иногда называют аберрацией главного луча. Если на входной зрачок объектива (рис. 6.17) под углом а к его оси падает параллельный пучок лучей, то после объектива, имеющего только одну аберрацию — дисторсию, пучок лучей останется гомоцентрическим и построит изображение А' некоторой удаленной точки. В этой же ситуации идеальный объектив построит изображение Ао' той же самой точки. Вследствие дисторсии главный луч, идущий через центр входного зрачка, «привел» пучок не в точку А'о, а в точку А'. Положение точки А' определено ходом луча, проходящего через главные точки объектива (НН' — главные плоскости, Fq — задний параксиальный фокус объектива). Отрезок Δу' = у' – у0 = у' —ƒо tg α> называется дисторсией объектива, выраженной в линейной мере.
Дисторсия может быть выражена в относительных единицах (процентах
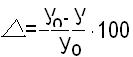
6.15)
6.6.3. Измерение разрешающей способности
Для измерения разрешающей способности оптических систем используют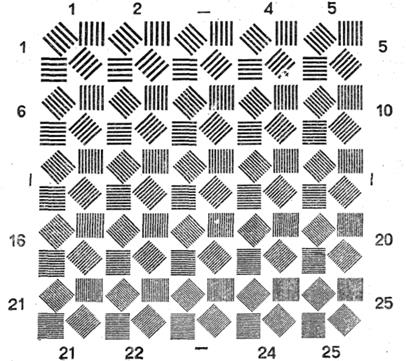 
штриховые или радиальные миры. Штриховые миры представляют собой стеклянные пластины с нанесенными на них темными штрихами на светлом фоне (рис. 5.18). В промышленности выпускают шесть номеров стандартных штриховых о мир, каждая из которых состоит из 25 элементов с цифровой характеристикой по краям. Один элемент состоит из четырех групп штрихов: с вертикальным, горизонтальным направлением и под углом 45° в двух взаимно перпендикулярных направлениях, Ширина линии в каждой мире убывает от элемента к элементу по закону геометрической прогрессии со знаменателем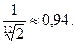 
Ширина линии ℓ = 2а, где а – ширина светлого штриха, мм.
Угловое расстояние ширины линии миры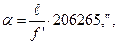 
где f’ – фокусное расстояние объектива коллиматора, мм.
Число полос (линий) на один миллиметр для любого номера элемента данной миры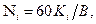 
где i = 1; 2; 3... 25; В – база миры, мм, определяемая расстоянием между штриховыми отметками на мире. Вместо цифр 3, 11. 15 и 23, соответствующих номерам элементов миры, нанесены штриховые отметки. Мира имеет таблицу для расшифровки, которой указаны значения разрешающей способности для каждого элемента.
Радиальные миры (рис. 6.19) представляют собой круг из стекле или фотобумаге, который разделен на 36 или 72 белых (прозрачных) и черных (непрозрачных) секторов. На любом радиусе ширина белых и черных секторов одинакова. И те и другие миры имеют абсолютный контраст К = 1. Практически прозрачности светлых штрихов или секторов должна быть больше прозрачности фона в 100 раз. Для специальных исследований применяют миры разного контраста.
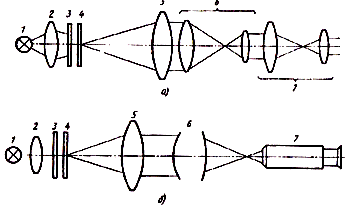
Разрешающую способность измеряют визуальным и фотографическим способами. Визуальный способ используется для контроля отдельных объективов визуальных приборов, телескопических систем. Визуальную разрешающую способность при этом способе измеряют на оптической скамье с помощью зрительной трубы для телескопических систем (рис. 6.11, а) и с помощью микроскопа для отдельных объективов (рис. 6.11, б). В фокальной плоскости объектива 5 коллиматора помещают тест-объект 4 в виде штриховой или радиальной миры, освещаемой источником света 1 через конденсор 2 и матовое стекло 3. Изображение миры, спроецированное в плоскость наилучшего изображения контролируемой системы 6, рассматривают с помощью зрительной трубы 7 (рис. 6.11, а) или микроскопа 7 (рис. 6.11, б) и определяют номер элемента штриховой миры, разрешаемой по всем четырем направлениям, или максимальный размер кружка размытия радиальной миры.
Плоскость наилучшего изображения определяют перемещением зрительной трубы или микроскопа вдоль оптической оси до получения наиболее резкого изображения миры. Увеличение зрительной трубы выбирают из условия, позволяющего исключить влияние ограниченности разрешающей способности глаза наблюдателя на результаты измерений. Числовая апертура микроскопа должна быть больше апертуры испытуемого объектива или равна ей.
Перед измерениями коллиматор оптической скамьи должен быть выставлен на бесконечность и оптическая ось контролируемой системы (телескопической или объектива) совмещена с оптической осью коллиматора. Фокусное расстояние объектива коллиматора f к должно быть в 3 – 5 раз больше фокусного расстояния контролируемой системы.
Разрешающая способность системы, контролируемой по штриховой мире, мм-1,
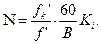(6.16)
Значение Ki выбирают из таблицы; f ' – фокусное расстояние контролируемой системы.
Разрешающая способность объектива, контролируемого по радиальной мире, мм-1,
N = m/(πd), (6.17)
где m – число пар темных и светлых секторов миры; d – наибольший размер кружка размытия миры.
Дата добавления: 2015-07-10; просмотров: 227 | Нарушение авторских прав