Рентгеновские источники РФС 4 страница

В целом, чем больше значения Р и I, тем точнее система ОС отрабатывает черты сканируемой поверхности и тем достовернее данные, получаемые при сканировании. Однако при превышении некоторых критических значений I (индивидуальных для каждого конкретного случая) самовозбуждение системы ОС на низких частотах приводит к появлению сильного шума в сигнале V_err и как следствие к появлению ложных осцилляции на профиле скана (рис. 5.25).

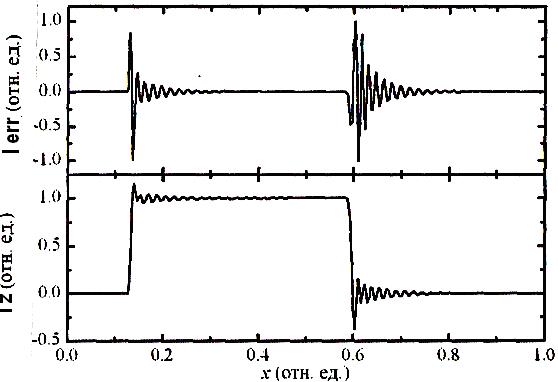
Рис. 5.25 – Самовозбуждение ОС вследствие завышения интегральной постоянной ОС I. (Вверху) сигнал ошибки V_err, (внизу) сигнал на Z-сканере V_z, соответствующий измеренному рельефу при сканировании ступеньки поверхности тестового образца. Сравнить с рис. 5.12

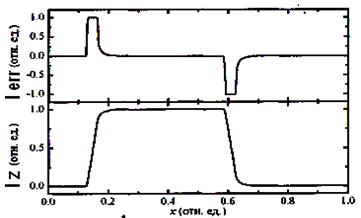
В то же время при малых значениях Р и I система ОС не успевает отрабатывать резкие черты топографии. Недостаточно большое значение I приводит к искажению изображения краев ступеней – происходит сглаживание резких деталей рельефа (рис. 5.13). В сигнале ошибки это проявляется в большой амплитуде выбросов при прохождении краев ступеней и затягивании задних фронтов выбросов. Сканирование образца с резкими деталями рельефа при недостаточно большом I может привести к поломке зонда и сканера.

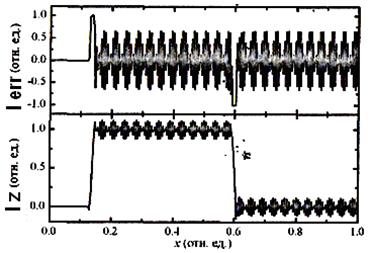
Увеличение параметра D повышает стабильность ОС при сканировании шероховатых образцов. Однако при завышении параметра D происходит самовозбуждение на высоких частотах (рис. 5.14). При сканировании гладких образцов следует установить D = 0.

5.6.5. Факторы, влияющие на качество изображения АСМ

В результате сканирования поверхности образца с помощью СЗМ удается построить трехмерное изображение рельефа поверхности. Разрешающая способность микроскопа в направлениях X,Y и Zопределяется различными факторами.

Разрешение по оси Z ограничивается чувствительностью оптического датчика смещений и амплитудой паразитных механических вибраций зонда относительно поверхности образца. Конструкция микроскопа обеспечивает уменьшение амплитуды этих вибрации до долей ангстрема.

Несколько факторов оказывают влияние и на разрешение в плоскости X,Y. Прежде всего, таким фактором является точность позиционирования зонда, которая определяется ХУ-сканером. Большое значение имеет геометрия острия зонда. При сканировании деталей рельефа сравнимых по геометрическим размерам с характерными размерами зонда (радиус закругления R, угол при вершине зонда, определяемый отношением высоты зонда к его основанию L/W) качество получаемого изображения определяется геометрией острия (рис. 5.21, б). Однако при сканировании предельно плоских (атомарно-плоских) поверхностей разрешение лимитируется диаметром атома на самом конце зонда эффект последнего атома (рис. 5.21, в). Таким образом, макроскопическая геометрия зонда не является определяющей и удается получить атомное разрешение.

Качество/достоверность получаемого изображения рельефа поверхности также зависит от свойств исследуемой поверхности, которые оказывают влияние на взаимодействие между зондом и поверхностью.

Любая поверхность на воздухе покрыта тонким слоем адсорбированных атомов (толщиной 2-50 нм), состоящим из воды и следов веществ, с которыми образец находился в контакте в процессе изготовления, загрязнений и т. п. При соприкосновении зонда с адсорбционным слоем возникает сильная притягивающая компонента силы вследствие капиллярного эффекта. Это приводит к тому, что при одном и том же расстоянии зонд-образец сила взаимодействия зонда с образцом может быть меньше при приближении зонда, чем при его удалении (на экспериментальной кривой F® имеется гистерезис). Влияние сил капиллярного взаимодействия можно уменьшить при использовании острых зондов с малым R и большим L/W вследствие меньшей площади контакта с адсорбционным слоем.

Материал образца также оказывает влияние на характер сил взаимодействия между зондом и поверхностью. Поверхность некоторых материалов накапливает статическое электричество, которое существенно затрудняет измерения. Слишком мягкие образцы могут деформироваться под действием зонда.

5.6.6. Режимы и моды измерений АСМ

Условно методы получения информации о рельефе и свойствах поверхности с помощью АСМ можно разбить на две большие группы – контактные квазистатические и бесконтактные колебательные. В контактных квазистатических методиках острие зонда находится в непосредственном соприкосновении с поверхностью, при этом силы притяжения и отталкивания, действующие со стороны образца, уравновешиваются силой упругости кантилевера. При работе АСМ в таких режимах/модах используются кантилеверы с относительно малыми коэффициентами жесткости, что обеспечивает высокую чувствительность и позволяет избежать нежелательного чрезмерного воздействия зонда на образец.

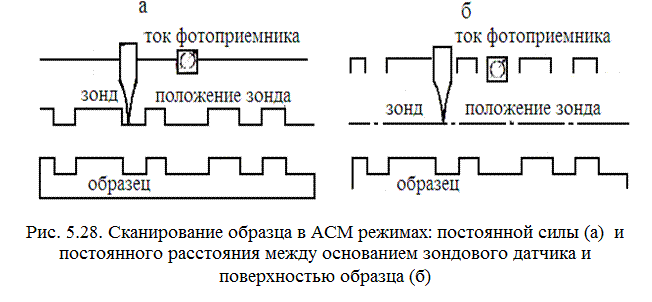
Изображение рельефа поверхности в контактной моде АСМ формируется либо в режиме постоянной силы, либо в режиме постоянного расстояния между основанием зондового датчика и поверхностью образца, которые используются для сканирования поверхностей с различными масштабами неровностей.

При сканировании образца в режиме F = const, система ОС, отслеживающая сигнал с фотоприемника ΔI_Z оптического датчика смещений, поддерживает постоянной величину изгиба кантилевера Δz = const, а значит и сила взаимодействия зонда с образцом остается постоянной. При этом

управляющее напряжение на Z-сканере пропорционально рельефу поверхности образца (рисунок 5.15, а).

Режим постоянной силы используется в случае, если характерный размер неровностей на поверхности образца превышает 1 нм.

В режиме постоянного расстояния между основанием зондового датчика и поверхностью (z = const) движение зондового

датчика происходит на некоторой средней высоте z_cp над образцом,

, при этом в каждой точке регистрируется изгиб кантилевера Δz, пропорциональный силе, действующей на зонд со стороны поверхности (рис. 5.28, б). АСМ изображение в этом случае характеризует пространственное распределение силы взаимодействия зонда с поверхностью. Этот режим используется при сканировании очень маленьких (не более 10x10 нм) моноатомно гладких областей с перепадами высот порядка единиц ангстрем для исследования строения поверхностных атомных сеток и моноатомных ступеней на поверхности кристаллов.

Кроме рельефа исследуемой поверхности, в контактной моде можно получить информацию о трибологических свойствах поверхности образца в нанометровом масштабе, регистрируя F_L – латеральную компоненту силы взаимодействия между зондом и образцом (Микроскопия Сил Трения, МСТ). Пространственное распределение коэффициента трения между поверхностью и движущимся над ней зондом формируется путем регистрации кручения кантилевера (разностного сигнала левого и правого секторов фотодетектора ΔI_L). В процессе сканирования на зонд действует сила трения со стороны поверхности образца F_тр = μΝ, где N – сила реакции, действующая на зонд со стороны образца, μ – локальный коэффициент трения. Кантилевер испытывает деформацию кручения, что приводит к разбалансу освещенности левого и правого секторов фотодетектора ΔI_L. Чем больше μ, тем больше изгиб кантилевера и тем больше ΔI_L. Обычно исследование пространственного распределения коэффициента трения и рельефа поверхности производится одновременно (сигналы от всех секторов фотодетектора регистрируются одновременно).

Следует отметить, что значение локального коэффициента трения может существенно отличаться от известных значений коэффициентов сухого трения, приведенных в справочниках, вследствие принципиально различных механизмов сухого трения поверхностей макроскопических тел и взаимодействия зонда с образцом. В первом случае существенную роль в возникновение силы трения играет зацепление микроскопических неровностей поверхностей. Во втором случае размер области контакта зонда с поверхностью составляет 0,1 – 1 нм, т. е. намного меньше обычного размера неровностей.

В формировании МСТ изображения существенную роль играет взаимодействие зонда с резкими деталями рельефа (например, краем ступени), приводящее к появлению топографических артефактов. Для распознавания топографических артефактов необходимо регистрировать МСТ сигнал в двух направлениях движения зонда: прямом и обратном. Знак латеральной компоненты, связанной с особенностями рельефа, зависит только от локального наклона поверхности и не зависит от направления движении зонда, поэтому артефакты топографии при прямом и обратном сканировании будут иметь одинаковый контраст. Направление силы трения всегда обратно по отношению к направлению движения, поэтому контраст, обусловленный локальными изменениями коэффициента трения, на изображениях при прямом и обратном сканировании будет инверсным по отношению друг к другу.Благодаря топографическому артефакту края резких деталей рельефа в МСТ изображении кажутся подчеркнутыми (эффект оконтуривания).

Это широко используется для выявления моноатомных ступеней, краев плоских дефектов и других подобных объектов на поверхности твердого тела, а также для получения атомного разрешения в контактной моде.

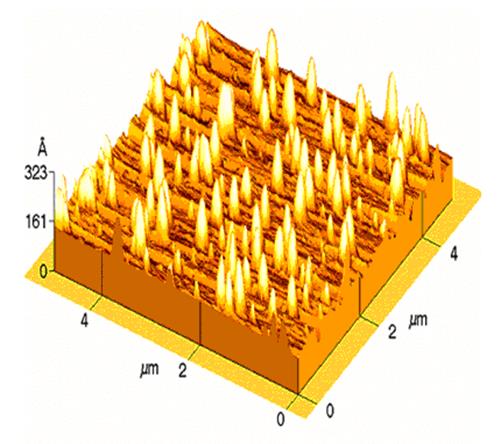
Рис.5.29. Изображение поверхности кремния на различных стадиях окисления

На рис.5.29 приведен пример зондирования поверхности кремния на различных стадиях окисления методом атомно-силовой микроскопии.

6 ХАРАКТЕРИСТИКИ КАЧЕСТВА ИЗОБРАЖЕНИЯ ОПТИЧЕСКИХ ПРИБОРОВ

6.1 Критерии качества оптического изображения

Реальная оптическая система создает изображение предмета с определенными искажениями. Отличия изображения от предмета возникают вследствие аберраций оптической системы, дифракционных явлений, дефектов изготовления и других факторов.

Характеристикой качества изображения служат аберрации различных видов в зависимости от поставленной задачи. Оптические системы с большими аберрациями характеризуют, как правило, геометрическими аберрациями, а для систем с малыми аберрациями оказывается более удобным использование волновых аберраций.

Геометрической аберрацией называется отклонение значений координат лучей, вычисленных для реальной системы, от значений координат тех же лучей, вычисленных для идеальной системы. Геометрические аберрации делят на монохроматические, которые возникают при прохождении через систему лучей света одной длины волны, и хроматические, возникающие при прохождении через систему лучей с различной длиной волн (белый свет).

К монохроматическим аберрациям относятся сферическая (продольная и поперечная), кома, астигматизм, кривизна поля и дисторсия; к хроматическим – хроматизм положения и хроматизм увеличения.

Волновой аберрацией оптической системы называется отклонение реального волнового фронта от поверхности сравнения: сферы для фотографических объективов, объективов телескопов и других объективов; плоскости для телескопических систем.

Волновая аберрация выражается в единицах длины волн. Если волновая аберрация меньше 0,1λ или равна ей, то изображение точки можно считать идеальным. Если волновая аберрация равна 0,25λ, то изображение считают хорошим. Указанные пределы определены английским физиком Рэлеем и получили название критериев Рэлея.

Аберрации измеряют в реальных оптических системах для определения соответствия их расчетным данным и для установления влияния каждой аберрации на качество изображения. В зависимости от назначения оптической системы аберрации измеряют в угловой мере (в основном для зрительных труб и прожекторных зеркал) или в линейной (в фотографической оптике). Волновые аберрации измеряют в астрономической и микроскопической оптике, для спектральных призм и т. п.

Аберрации вместе с неизбежными погрешностями изготовления оптических деталей и сборки оптических систем снижают качество изображения.

Характеристики качества изображения зависят от требований, предъявляемых к оптической системе прибора. Например, оптические системы астрономических приборов, имеющих небольшое поле и изображающих в основном бесконечно удаленные предметы, должны быть рассчитаны с минимальными аберрациями. Изображение, создаваемое такими системами, искажается вследствие дифракции. Качество изображения оптических систем, применяемых с различными приемниками (глаз, фотоматериал, электронно-лучевые трубки, электронно-оптические преобразователи) и создающих изображение с большим полем, которое затем рассматривают визуально (визуальные, проекционные, фотографические, телевизионные и другие устройства), характеризуется резкостью, степенью соответствия геометрического подобия и подробностей структуры различных предметов и их изображений, а также контрастом. Оптические системы, используемые в оптико-электронных приборах для передачи световой энергии в целях дальнейшего преобразования ее в электрические сигналы, характеризуются количеством световой энергии и ее распределением в изображении элементарных объектов (светящейся точки, линии).

На основании изложенного критерии оценки качества оптического изображения, для различных систем выбирают в зависимости от выполняемых ими задач. Критериями оценки качества оптического изображения, адекватными перечисленным характеристикам, являются функция рассеяния, пограничная кривая и оптическая передаточная функция. Все три критерия взаимообратимы, взаимосвязаны и взаимозаменяемы, но не одинаково удобны при использовании для оценки качества изображения различных оптических систем.

Эти критерии могут быть получены из математического уравнения процесса образования оптической системой изображения, показывающего зависимость между распределением освещенности Е(х', у') в изображении и распределением яркости L(х, у) в предмете. Если предмет рассматривать как совокупность светящихся точек, то уравнение процесса образования изображения при некогерентном излучении предмета будет иметь вид

(6.1)

Изменение распределения освещенности в плоскости изображения в указанном случае обусловливается передающими свойствами оптической системы, которые характеризуются качеством изображения бесконечно удаленной светящейся точки (при условии соблюдения изопланатичности оптической системы). Функция А(х' – х*, у' – у*) есть функция распределения освещенности в изображении любой светящейся точки бесконечно удаленного предмета с координатами х, у, называемая функцией рассеяния оптической системы. Текущие координаты х*, у* точки в плоскости изображения определяют по формулам х* = βх, у* = βу, где β – линейное увеличение оптической системы. Уравнение (6.1) представляет собой свертку функций А и L, поэтому его можно выразить через преобразование Фурье. Тогда уравнение процесса образования изображения можно записать так:

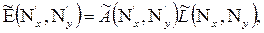(6.2)

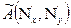где , и 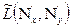– преобразования Фурье функций соответственно распределения освещенности в изображении 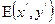, рассеяния оптической системы и распределения яркости 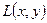в предмете; N'_x и N'_y – пространственные частоты, равные обратному значению периода синусоидального изменения освещенности в пространстве изображения по двум взаимно перпендикулярным направлениям; N_x и N_y – пространственные частоты, равные обратному значению периода синусоидального изменения яркости в плоскости предмета по тем же направлениям.

Пространственные частоты в плоскости предмета и в плоскости изображения связаны зависимостью N' – βN.

Уравнение (6.2) выражает процесс образования изображения в пространственно-частотном представлении.

Рассмотрим каждый из критериев отдельно и определим их связь с характеристиками качества изображения, создаваемого оптической системой.

6.2 Функция рассеяния

Функция рассеяния А(х', у') – это распределение освещенности в изображении бесконечно удаленной светящейся точки в плоскости наилучшего изображения, представляющее собой дифракционную картину. Математическое выражение функции рассеяния А(х', у') для безаберрационной оптической системы имеет вид

.

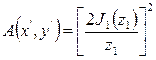Здесь J₁(z₁) – функция Бесселя первого рода первого порядка; аргумент где D – диаметр входного зрачка оптической системы; f ' – фокусное расстояние; λ – длина волны; 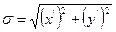– расстояние от центра пятна рассеяния; х', у' – текущие координаты в плоскости изображения.

Картина ФРТ для безаберрационной оптической системы (рис.6.1) состоит из центрального максимума диаметром 1.22 канонических единиц и побочных максимумов – колец с шагом, постепенно приближающимся к 0.5 канонических единиц. Безаберационная ФРТ симметрично относительно оптической оси. Центральный максимум содержит 83.8% всей энергии (его высота равна единице), первое кольцо – 7.2% (высота 0.0175), второе 2.8% (высота 0.0045), третье 1.4% (высота 0.0026), четвертое 0.9%.

Рис.6.1. Функция рассеяния точки в отсутствие аберраций

Центральный максимум ФРТ называется диском Эри (Airy). Диаметр диска Эри в реальных координатах на изображении:

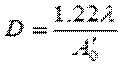, (6.1)

где – апертура осевого пучка.Диск Эри в общем случае может быть не круглым, если меридиональная и сагиттальная 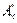апертуры различны.

6.2.1 Влияние неравномерности пропускания по зрачку на ФРТ

На рис.6.2 показан вид ФРТ для различных функций пропускания. Если пропускание уменьшается к краям зрачка (2), то центральный максимум ФРТ расширяется, а кольца исчезают. Если пропускание увеличивается к краям зрачка (3), то центральный максимум сужается, а интенсивность колец увеличивается. Эти изменения по-разному влияют на структуру изображения сложного объекта, и, в зависимости от требований, используются различные функции пропускания, “накладываемые” на область зрачка. Это явление называется аподизацией.

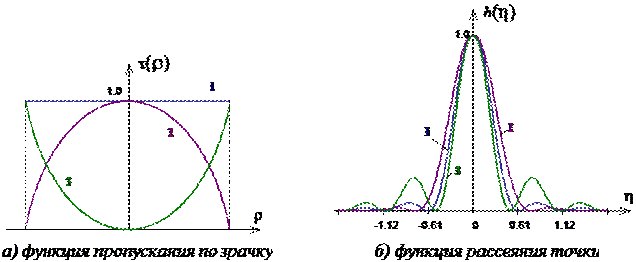
Рис.6. 2 - Влияние неравномерности пропускания по зрачку на ФРТ

В реальных оптических системах при наличии остаточных аберраций происходит перераспределение световой энергии между центральным кружком и светлыми кольцами, Особенно сложной дифракционная картина получается в изображении внеосевой точки поля. Поэтому за критерий оценки качества изображения оптических систем с небольшим полем и для исследований по центру поля принимают функцию рассеяния.

6.2.2. Влияние аберраций на ФРТ и ОПФ

Влияние малых аберраций (волновая аберрация составляет доли длин волн) на ФРТ проявляется в том, что часть энергии из центрального максимума переходит в кольца. В результате в центральном максимуме остается около 60-70% вместо 84%, при этом размеры центрального максимума сохраняются, а интенсивность в центре уменьшается (рис.6.3).

Рис.6.3. Влияние аберраций на ФРТ.

Аберрации разных типов по-разному влияют на вид пятна рассеяния (картину Эри). В случае симметричных аберраций (расфокусировка, сферическая) сохраняется радиальная симметрия пятна (рис. 6.4а). В случае несимметричных аберраций (кома, астигматизм) симметрия пятна нарушается (рис. 6.4б, рис. 6.4в).

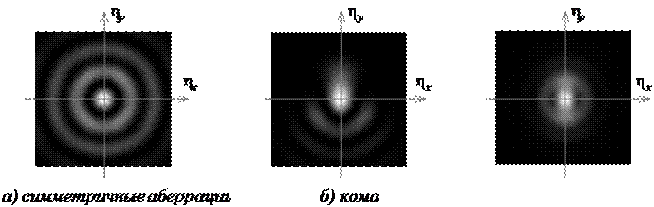
Рис.6.4. Картины Эри для аберраций различных типов

При дальнейшем увеличении аберраций сходство ФРТ с безаберрационной полностью теряется, и ее форма определяется картиной поперечных аберраций (точечной диаграммой). Практически вся энергия из центрального максимума перекачивается в кольца (в центральном максимуме остается меньше 40% энергии). Однако при этом сохраняется дифракционный узор с шагом 0.5 в канонических координатах.

6.2.3. Число Штреля

Поскольку при малых аберрациях часть энергии из центрального максимума перекачивается в кольца, уменьшается интенсивность в центральном максимуме. Обозначим значение ФРТ в ее максимуме при отсутствии аберраций h₀(0), а при наличии аберраций h(0) (рис. 6.5).

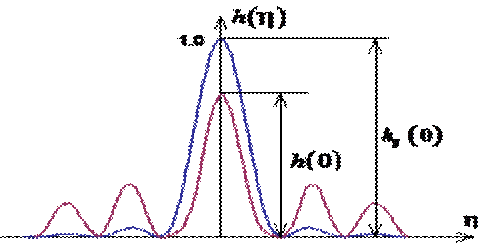
Рис.6.5. Число Штреля.

Число Штреля (критерий Штреля, Strehl ratio) показывает влияние аберраций на ФРТ:

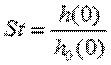. (6.2

Значение числа Штреля находится в пределах , энергия в кольца перекачивается в таком же соотношении. Если – оптическая система безаберрационная, если 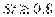– система

практически безаберрационная, поскольку уменьшение центрального максимума на 20% почти незаметно. Понятие функции рассеяния распространяют и на распределение освещенности в изображении светящейся линии. Функция А_л(х', у') рассеяния линии есть результат интегрирования функции А (х', у') рассеяния точки по некоторому направлению, например у. Тогда

По виду функции рассеяния определяют наличие аберраций и дефекты изготовления и сборки деталей оптической системы.

Для производственного контроля оптических систем по функции рассеяния используют различные числовые критерии: размер центрального кружка пятна рассеяния, диаметр пятна рассеяния с определенным содержанием световой энергии, количество которой устанавливается в зависимости от требований, предъявляемых к оптической системе; коэффициент штреля (определительная яркость) – процентное отношение освещенности в центре пятна рассеяния данной системы к освещенности в центре пятна рассеяния идеальной оптической системы с теми же параметрами.

6.3. Пограничная кривая

Кривая распределения освещенности в изображении пограничного теста Е_п(х’) называется пограничной кривой. Эта кривая характеризует распределение освещенности в изображении объекта, представляющего собой границу светового и темного поля. Такой объект называют пограничным тестом. Распределение яркости L_n(x) в нем описывается функцией скачка (рис. 5.3, а), которая является одномерной функцией. Для контраста, равного единице,

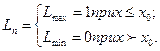
Математическое выражение пограничной кривой:

(5.3)

Связь между пограничной кривой Е_п(х') и функцией А_л(х^’) рассеяния линии можно определить по формуле (5.3):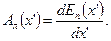

Графически пограничная кривая изображена на рис.5.3,б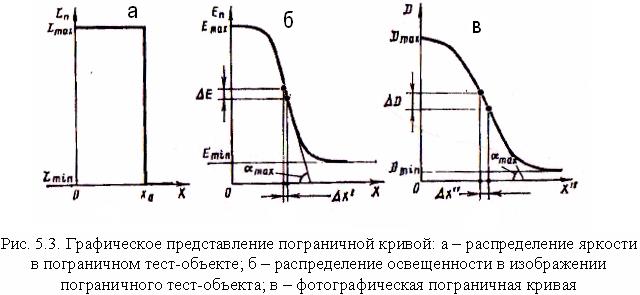

График пограничной кривой наглядно свидетельствует о понижении резкости изображения, которая является одним из основных признаков качества визуального изображения. Наклон пограничной кривой зависит от размера пятна рассеяния. Чем меньше крутизна пограничной кривой, тем больше размер пятна рассеяния и тем хуже резкость изображения. Следовательно, угол наклона пограничной кривой характеризует качество изображения по резкости. Пограничную кривую как критерий оценки качества изображения используют для систем, создающих визуальное изображение с большим полем. Кроме того, ее можно применить для непосредственной оценки качества изображения сложных систем, состоящих из объектива и различных приемников. Например, кинофотоприборы можно проверить по фотографической пограничной кривой,
т. е. получить зависимость плотности и почернения светочувствительного слоя от координат х" в плоскости фотопленки (см. рис. 5.3, в).

Объективно качество изображения можно количественно оценить по пограничной кривой с помощью числовых критериев, приведенных ниже.

Пограничный градиент G_max – тангенс угла α_max наклона касательной в средней точке пограничной кривой к оси абсцисс (см. рис. 5.3, б), характеризующий резкость изображения, или G_{ф mах} – то же для фотографической пограничной кривой (см. рис. 5.3, в):

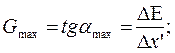
где ΔЕ – приращение освещенности оптического изображения пограничного теста; ΔD – приращение плотности D почернения фотографического изображения пограничного теста; Δх' и Δх" – интервалы на оси абсцисс.

Критерий р, учитывающий перепад максимальной и минимальной освещенности, или критерий р _ф плотности почернения фотопленки, характеризующий резкость и контраст изображения:

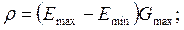
Пограничная нерезкость S – отношение площади Q₁, ограниченной фотографической пограничной кривой D(х”), к площади квадрата Q₀, принятой за 100 % (рис. 5.4):

Пограничная кривая по сравнению с функцией рассеяния более удобна для оценки качества изображения при испытании оптических систем с большим полем, но менее удобна для оценки качества изображения при расчетах.

6.4. Оптическая передаточная функция (ОПФ)

В последнее время как основной критерий оценки качества сложных оптических систем (в том числе и объективов с большим полем), предназначенных для передачи информации, широкое распространение получила оптическая передаточная функция (ОПФ). Она служит мерой способности оптической системы воспроизводить различные простра-нственные частоты. Любой пред-мет, изображаемый оптической системой, можно описать функцией распределения яркости L(х, у), и эту функцию, согласно преобразованиям Фурье, можно разложить на отдельные синусоидальные составляющие с изменяющимися пространственными частотами, которые характеризуются амплитудой (интенсивностью све та) и фазой (угловой ориентацией на плоскости), зависящими от пространственной частоты. Например, функцию распределения яркости в прямоугольной решетке (рисунок 6.8) можно представить набором синусоид 1 – 4 с различными амплитудами и периодами. Изображая такой предмет, оптическая система передает каждую из составляющих с различными периодами ρ с искажениями по амплитуде а и фазе. Значение этих искажений можно выразить функциями от пространственной частоты Т(N_x, N_v) и φ(N_x, N_y). Они зависят от остаточных аберраций, дифракционных явлений и погрешностей изготовления оптической системы, т. е. изменяются от тех факторов, которые определяют качество изображения.

Рассматривая уравнение процесса образования изображения в частотном представлении (6.2), можно определить эту меру искажений как отношение функций распределения освещенности в изображении к функции распределения яркости в предмете: 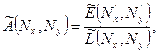которая представляет собой ОПФ.

Дата добавления: 2015-07-10