Исчисление предикатов. Оно позволяет включать в выражения переменные

Оно позволяет включать в выражения переменные. Переменные позволяют создать обобщенные утверждения относительно классов логических объектов. В логике предикатов в дополнении к средствам логики высказываний вводятся логические операторы (квантор общности - для всех, квантор существования 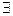- для некоторых). Переменная, входящая в область действия квантора, является связанной. Переменная, не являющаяся связанной, называется свободной. Подлинная переменная – только свободная переменная. Связанные переменные – фиктивные.

Примеры: ( х)Р(х) – всякий х обладает свойством Р. (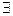 х)Р(х) – некоторый х обладает свойством Р и тд.

Исчисление предикатов 1 порядка позволяет связывать законом квантора переменные, соответствующие объектам из предметной области, но не предикаты или функции.

Примеры: 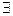x(persons(x)^likes(x,apples) некоторые люди любят яблоки.

Возможность логически выводить новые правильные выражения из набора истинных утверждений – важное свойство исчисления предикатов. Выражение Х логически следует из набора выражений S исчисления предикатов, если каждая интерпретация, которая удовлетворяет S, удовлетворяет Х.Если система правил вывода способна произвести каждое выражение, которое может логически следовать из S, то система правил вывода является полной. Если каждое предложение Х, полученное с помощью некоторого правила вывода на множестве S логических выражений также логически следует из S, то говорят, что это правило вывода обоснованно.

1. modus ponens Согласно этому правилу, если предложение P->Q, то можно вывести Q (может быть применено к переменным).

2. modus tollens P->Q, если Q – ложно, то предложение позволяет вывести 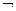Р.

3. исключение «И» Позволяет вывести истинность обоих конъюнктов на основе истинности конъюнктивного предложения. P и Q – истинны => P^Q – истина.

4. универсальное инстанциирование Если любую переменную, стоящую под квантором всеобщности в истинном предложении, заменить любым соответствующим термином из области определения, то результирующее выражение истинно. Т.о. если А принадлежит той же области определения, что и Х, и ( Хр)Р(Х), то можно вывести Р(А).

Правило резолюции – берутся 2 выражения и выражаются новые выражения, содержащие все литералы 2х первоначальных выражений, за исключением 2х взаимообратных литералов.

Унификация – это алгоритм определения необходимых подстановок с целью приведения в соответствие 2х выражений исчисления предикатов. Переменные, стоящие под знаком квантора существования, можно устранить из предложений в БД, заменив константами, обеспечивающими истинность предложения. Процесс удаления переменных, связанных квантором существования, усложнен фактом, что значения этих подстановок могут зависеть от значения других переменных в выражении.

Сколемизация – замена каждой переменной, связанной квантором существования, функцией нескольких или всех имеющихся в предложении переменных, которые возвращают соответствующую константу.

Два правила алгоритма резолюции нисходящим методом: 1. в 1ой выполненной резолюции следует использовать только что добавленное отрицание фразы. 2. в каждой последней резолюции должна участвовать резольета предыдущей резолюции.

Дата добавления: 2015-07-10