
Читайте также:
|
Проблема представления знаний.
Две наиболее фундаментальные проблемы для разработчиков систем на основе искусственного интеллекта: представление знаний (связана с проблемой получения и хранения знаний с помощью формального языка) и поиск (это метод решения проблемы, в котором систематически просматривается пространство состояний задачи, т.е. альтернативные стадии ее решения).
Предметные знания содержат данные о предметной области и способы преобразования этих данных при решении постановленных задач. По отношениям к предметным знаниям знания о представлении и знания об управлении являются метазнанями. В предметных знаниях можно выявить так называемые описатели. Описатели содержат определенную информацию о предметных знаниях. Например, коэффициент определенности правил и данных
Решение проблемы представления знаний предусматривает ответ на следующие вопросы:
1. какими должны быть состав и структура знаний?
2. какова должна быть форма представления знаний?
3. как построить алгоритм поиска решений в соответствии с тем или иным представлением знания?
Исчисление высказываний.
Символы P, Q, R, S. True (истины). False (ложь). Логические связки 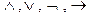 .
.
Пропозиционные символы – высказывания или утверждения относительно некоторого мира.
Предложения исчисления высказываний:
1. каждый логический символ и символ истинности является предложением,
2. отрицание предложения – это тоже предложение, 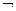 false,
false,
3. логическое умножение (конъюнкция) или операция «И» двух предложений – это тоже предложение,
4. тоже самое относительно логического сложения (дизъюнкции),
5. импликация, эквивалентность – предложения,
6. выражение вида P^Q, P и Q – конъюнкты,
7. P 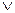 Q, P и Q – дизъюнкты,
Q, P и Q – дизъюнкты,
8. P 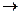 Q, P – предпосылка, Q – заключение (логическое следствие).
Q, P – предпосылка, Q – заключение (логическое следствие).
Выражение является предложением или правильно построенной формулой исчисления высказываний тогда и только тогда, когда оно может быть сформулировано в виде некоторой последовательности допустимых символов, согласно установленным правилам (true – T, false – F):
1. определение истинности конъюнкции ^ осуществляется следующим образом: высказывание имеет значение Т, если оба конъюнкта имеют значение Т, иначе F,
2. определение истинности дизъюнкции 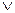 : высказывание имеет значение F только тогда, когда оба дизъюнкта имеют значение F, иначе Т,
: высказывание имеет значение F только тогда, когда оба дизъюнкта имеют значение F, иначе Т,
3. определение истинности импликации 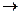 : высказывание имеет значение F только тогда, когда предпосылка принимает значение Т и значение истинности следствия = F, иначе – Т,
: высказывание имеет значение F только тогда, когда предпосылка принимает значение Т и значение истинности следствия = F, иначе – Т,
4. определение истинности эквивалентности: высказывание имеет значение Т только тогда, когда оба выражения имеют одинаковые значения истинности для всех возможных интерпретаций, иначе – F,
Таблица истинности содержит все возможные варианты значения истинности для элементарных суждений (атомарных формул), составляющих большие выражения, и задает значение истинности для каждой возможной интерпретации. Таблица истинности для оператора ^ (и) (рис.1). Тождественность выражений P 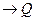 и
и 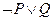 (рис.2).
(рис.2).
| P | Q | P^Q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
| P | Q | 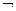 P P
| 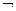 P P 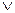 Q Q
| P->Q | (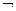 P P 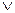 Q) Q) 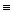 (P->Q) (P->Q)
|
| T | T | F | T | T | T |
| T | F | F | F | F | T |
| F | T | T | T | T | T |
| F | F | T | T | T | T |
1. 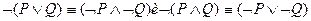 закон Моргана
закон Моргана
2. 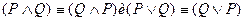 закон коммутативности
закон коммутативности
3. 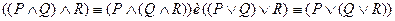 ассоциативный закон
ассоциативный закон
4. 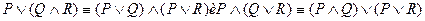 дистрибутивный закон
дистрибутивный закон
5. 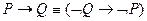 закон контрпозиции и импликации
закон контрпозиции и импликации
Дата добавления: 2015-07-10; просмотров: 104 | Нарушение авторских прав