Спектры непериодических сигналов

Любой непериодический сигнал можно рассматривать как периодический с периодом, стремящимся к бесконечности (Т→∞), но ограниченным во времени. Ограниченный во времени сигнал называется финитным.

Представителем таких финитных сигналов, имеющих бесконечный период, может быть одиночный импульс:

Аналитическое описание этого сигнала имеет вид:

Для оценки спектров таких сигналов используется интегральное преобразование Фурье (прямое преобразование Фурье):

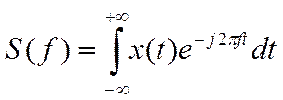
Определим спектр этого импульса:

Используем формулу Эйлера: .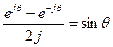

Следовательно, спектр импульса будет описываться выражением

???

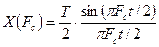
Спектр одиночного импульса описывается следующей формулой:

Иначе эта функция называется функцией sinc.

В таком спектре гармоники очень плотно следуют друг за другом, т.е. спектр сигнала становится сплошным.

Чем меньше длительность импульса, тем шире спектр.

График функция sinc имеет следующий вид.

Последовательность униполярных прямоугольных импульсов

b_n = 0 - четная функция.

;

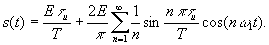
Для перехода от спектральной формы сигнала к временной форме, используется обратное преобразование Фурье:

Представленные два интеграла (прямое и обратное преобразования Фурье) называются парой преобразований Фурье.

Дата добавления: 2015-07-10