Спектры периодических сигналов

Спектральное представление сигналов

Любой сигнал считается дуальным, т.е. он имеет двойственное представление, одновременно он существует как в области времени, так и в частотной области. При этом если заранее известно временное представление сигнала и его характеристики, то можно найти его спектр и наоборот – по спектральному представлению сигнала можно определить временное представление.

Спектр периодического сигнала является дискретным и представляет набор гармонических колебаний, в сумме составляющий исходный сигнал. Одним из преимуществ разложения сигнала в спектр является следующее. Сигнал, проходя по каналу, претерпевает изменения (усиление, задержка, детектирование, изменение фазы, ограничение и т. д.). Токи и напряжения в цепи под действием сигнала описываются дифференциальными уравнениями, соответствующими элементам цепи и способу их соединения. Линейные цепи описываются линейными дифференциальными уравнениями, причем для линейных цепей верен принцип суперпозиции, согласно которому действие на систему сложного сигнала, состоящего из суммы простых сигналов, равно сумме действий от каждого составляющего сигнала в отдельности. Это позволяет при известной реакции системы на какой-либо простой сигнал, например, на синусоидальное колебание с определенной частотой, определить реакцию системы на любой сложный сигнал, разложив его в ряд по синусоидальным колебаниям.

Гармонический ряд Фурье может быть представлен в следующих видах:

(2.3)

где

A_n - амплитуда гармоник, nw₁ - частота гармоник, j_n - фаза гармоник, - комплексная амплитуда гармоник. При выбранном знаке перед j_n фаза гармоник является аргументом комплексной амплитуды. Все виды разложения тождественны и переходят один в другой.

Любой периодический сигнал, какой бы он сложной формы ни был, согласно теореме Фурье можно представить в виде бесконечного ряда из отдельных гармонических составляющих:

,

где .

Представленный ряд содержит синусоидальные и косинусоидальные составляющие, причем эти составляющие ( и ) повторяются в соответствии с частотой повторения, равной . Вторые составляющие – с удвоенной частотой, третьи – с утроенной и т.д.

Первые составляющие называются основной частотой, основной гармоникой или фундаментальной частотой. Вторые составляющие называются вторыми гармониками и т.д.. этот ряд бесконечен, поэтому для более краткой записи используют следующую форму:

,

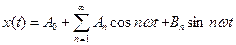где А₀ – среднее значение сигнала за период времени Т. Это постоянная составляющая переменного сигнала.

Таким образом, если заданы параметры любого периодического сигнала (известен период и изменение А во времени), то мы можем определить все коэффициенты ряда Фурье и представить сигнал в виде спектра.

Обычно сигнал сложной формы наблюдается при измерении вибрации, и относятся такие сигналы к классу случайных сигналов.

При обычных измерениях теплотехнических параметров на судовых установках сигналы относятся больше к классу монотонных. Кодовая комбинация, которая передается, уже относится к классу цифровых сигналов и также может быть представлена каким-то аналитическим описанием.

Все сигналы, которые используются в автоматических системах управления, являются казуальными (причинными). Поскольку мы занимаемся кодами, т.е. цифровыми сигналами, то в самом простейшем случае кодовую последовательность можно представить в виде последовательности прямоугольных импульсов, так называемых меандров.

Для нечетной функции s(t)= -s(-t) обращаются в ноль все коэффициенты a_n.

b_n = 0 для четных n = 0,2,4...

для нечетных n = 1,3,5...

Этот сигнал как периодический может быть представлен рядом Фурье:

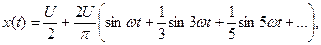
где .

Спектральный представление сигнала представляет собой ряд синусоид. По мере возрастания частоты амплитуда гармоник уменьшается. Спектр характеризует энергетическую емкость сигнала (энергетический состав). Из данного спектра видно, что в прямоугольный сигнал имеет основной энергетический вклад вносят первые пять гармоник. Это составляет примерно 95% энергии сигнала. Поэтому для передачи такого сигнала нет необходимости использовать частотный диапазон более широкий, чем 9×f.

Дата добавления: 2015-07-10