Показатели вариации

В практическом анализе оценка рассеяния значений признака может оказаться не менее важной, чем определение средней.

Самая грубая оценка рассеяния, определяемая по данным вариационного ряда, может быть дана с помощью размаха вариации:

, где х_тaх и х_тin — наибольшее и наименьшее значения варьирующего признака.

Этот показатель представляет интерес в тех случаях, когда важно знать, какова амплитуда колебаний значений признака, например, каковы колебания цены на данный товар в течение недели или по разным регионам в данный отрезок времени.

Однако этот показатель не дает представления о характере вариационного ряда, расположении вариантов вокруг средней и может сильно меняться, если добавить или исключить крайние варианты (когда эти значения аномальны для данной совокупности). В этих случаях размах вариации дает искаженную амплитуду колебания против нормальных ее размеров.

Для оценки колеблемости значений признака относительно средней используются характеристики рассеяния. Они различаются выбранной формой средней и способами оценки отклонений от нее отдельных вариантов. К таким показателям относятся: среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

Среднее линейное отклонение – среднее арифметическое из абсолютных значений отклонений отдельных вариант от их средней величины:

для несгруппированных данных: ;

для сгруппированных данных: ,

где x_i – значение признака в дискретном ряду или середина интервала в интервальном распределении;

f_i - частота признака.

Среднее линейное отклонение выражено в тех же единицах измерения, что и варианты или их средняя. Оно дает абсолютную меру вариации.

Чтобы избежать равенства нулю суммы отклонений от средней, можно вместо абсолютных отклонений использовать их квадраты. В этом случае мера вариации называется дисперсией.

Для несгруппированных данных: ;

для сгруппированных данных: .

Исчисление дисперсии сопряжено с громоздкими расчетами, которые можно упростить, если использовать следующую формулу:

.

Вследствие суммирования квадратов отклонений дисперсия дает искаженное представление об отклонениях, измеряя их в квадратных единицах. Поэтому на основе дисперсии вводят еще две характеристики: среднее квадратическое отклонение и коэффициент вариации.

Среднее квадратическое отклонение измеряется в тех же единицах, что и варьирующий признак, и исчисляется путем извлечения квадратного корня из дисперсии:

для несгруппированных данных: ;

для сгруппированных данных: .

Среднее квадратическое отношение, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные варианты признака от его среднего значения. Отклонение, выраженное в s, называется нормированным или стандартизированным.

Для оценки меры вариации и ее значимости используется коэффициент вариации, который дает относительную оценку вариации и получается путем сопоставления среднего квадратического отклонения со средним уровнем явления, результат выражается в процентах:

.

Так как коэффициенты вариации дают относительную характеристику однородности явлений и процессов, они позволяют сравнивать степень вариации разных признаков. Интерпретируется следующим образом: если V < 33%, то исследуемая совокупность однородная, средняя типичная; если V > 33%, то совокупность разнородная, средняя фиктивная, к ней следует относиться осторожно.

Пример. По приведенным данным таблицы смертности вычислить всевозможные показатели вариации:

Таблица 2. Расчетная таблица для исчисления показателей вариации.

Группы по возрасту	Мужчины fi	Середина интервала xi	Расчетные показатели
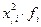
0-4
5-9
10-14
15-19
20-24
25-29
30-34
35-39
40-44
45-49
50-54
55-59
60-64
65-69
70 и старше
Итого				7166,3335	116960238,33

По выполненным расчетам вычисли показатели вариации:

Дисперсия:

или .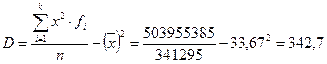

Среднее квадратическое отклонение: 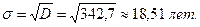, то есть в среднем возраст мужчин отклоняется от33,67 лет на 18,51 год.

Коэффициент вариации , так как больше 33%, следовательно, структура разнородная, средняя фиктивная, к ней надо относиться осторожно.

Дата добавления: 2015-07-12