Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Абсолютные показатели вариации

Читайте также:
  1. V11. Показатели эффективности и результативности профессиональной служебной деятельности секретаря суда.
  2. А) Глубину ассортимента характеризуют показатели, определяемые как произведение количества предлагаемых групп (видов) товаров на количество разновидностей в каждой группе;
  3. Абсолютные и относительные величины.
  4. Абсолютные показатели преломления алмаза и стекла соответственно равны 2,4 и 1,5. Каково отношение скоростей распростанения света в этих веществах?0,6
  5. Алгоритм 3. Записать коэффициенты разложения, основания степеней и показатели степеней в системе с основанием Q и выполнить все действия в этой самой системе.
  6. Браковочные показатели масла

Тема 7_2011-2012. Статистическое изучение вариации

Вопросы

  1. Понятие вариации. Абсолютные и средние показатели вариации.
  2. Показатели относительного рассеивания
  3. Виды дисперсии
  4. Анализ данных. Базовые показатели. Блочные диаграммы.
  5. Дисперсия альтернативного (качественного признака)

 

 

Вопрос 1. Понятие вариации. Абсолютные и средние показатели вариации

Различие (степень колебания) отдельных значений характеризуют показатели вариации.

 

Вариация – количественное изменение величины исследуемого признака в пределах однородной совокупности, которое обусловлено перекрещивающимся влиянием действия различных факторов.

 

 

Степень близости данных отдельных единиц хi к средней измеряется рядом абсолютных, средних и относительных показателей.

Абсолютные показатели вариации

Размах вариации R - это разность между наибольшим и наименьшим значением вариантов.

.

 

Применение понятий.

Размах выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска, вычислим, используя следующий упорядоченный массив

-6,1 -2,8 -1,2 -0,7 4,3 5,5 5,9 6,5 7,6 8,3 9,6 9,8 12,9 13,1 18,5

 

 

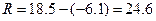
Размах позволяет измерить общий разброс данных. Его слабость в том, что он никак не учитывает, как именно распределены данные между минимальным и максимальным элементами.

 

Межквартильный размах (средний размах) – это разность между третьим и первым квартилями выборки.

 

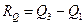, где Q1, Q3 – соответственно первый и третий квартили.

 

Эта величина позволяет оценить разброс 50% элементов и не учитывать влияние экстремальных элементов.

 

Применение понятий.

Межквартильный размах выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска, вычислим, используя следующий упорядоченный массив

-6,1 -2,8 -1,2 -0,7 4,3 5,5 5,9 6,5 7,6 8,3 9,6 9,8 12,9 13,1 18,5

 

Эта величина характеризует размах половины выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с высоким уровнем риска. Интервал, ограниченный числами 9,7 и 1,8 часто называют средней половиной.

 

Суммарные количественные характеристики, такие как медиана, первый и третий квартили, межквартильный размах, на которые не влияют выбросы, называются устойчивыми показателями.

 

Размах и межквартильный размах позволяют оценить общий и средний разброс значений, но они не учитывают как именно распределены данные. Дисперсия и стандартное (среднеквадратическое) отклонение лишены этого недостатка.

Дата добавления: 2015-07-12; просмотров: 198 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Величина итогового показателя не должна изменяться при замене индивидуальных значений признака средней величиной.| Средние показатели вариации
mybiblioteka.su - 2015-2024 год. (0.007 сек.)