
Читайте также:
|
Среднее линейное отклонение  определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учёта знака этих отклонений
определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учёта знака этих отклонений
 .
.
Дисперсия s2 (средний квадрат отклонений) определяется по формуле:
 ,
, 
Чем меньше дисперсия, тем лучше средняя арифметическая отражает собой всю представленную совокупность.
Среднее квадратическое отклонение s может быть найдено таким образом:
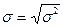 .
.
Дисперсия и среднее квадратическое (стандартное) отклонение позволяют оценить степень колебания данных вокруг среднего значения.
Интерпретация понятий
Дисперсия и среднее квадратическое (стандартное) отклонение позволяют оценить разброс данных вокруг среднего значения, т.е. сколько элементов выборки меньше среднего, а сколько – больше. Дисперсия обладает ценными математическими свойствами. Однако ее величина представляет собой квадрат единицы измерения (квадратный %, квадратный доллар и т.д.). Поэтому естественной оценкой дисперсии является стандартное отклонение, которое выражается в обычных единицах измерения - %, доллары …
Стандартное отклонение позволяет оценить величину колебания значений вокруг среднего значения. Практически во всех ситуациях наблюдаемые величины лежат в интервале плюс-минус одно стандартное отклонение от среднего значения. Поэтому, зная среднее арифметическое и среднее квадратическое (стандартное) отклонение можно определить интервал, которому принадлежит основная масса данных.
Применение понятий
Стандартное отклонение доходности 15 ВФ с очень высоким уровнем риска равно 6,62. Это значит, что доходность основной массы фондов отличается от среднего значения не более чем на 6,62%.
От 6,08-6,62=-0,54 до 6,08+6,62=12,7 в этом интервале есть 8 из 15 ВФ (53%)
Суммируем вышесказанное
ü Чем больший разброс имеют данные, тем больше их размах, межквартильный размах, дисперсия и стандартное отклонение
ü Чем более сконцентрированы данные, или однородны, тем меньше их размах, межквартильный размах, дисперсия и стандартное отклонение
ü Если все элементы выборки равны между собой (т.е. разброс отсутствует), межквартильный размах, дисперсия и стандартное отклонение равны нулю.
ü Ни одна из оценок изменчивости данных (размах, межквартильный размах, дисперсия и стандартное отклонение) не может быть отрицательной.
Применение понятий
Сравним разброс доходности ВФ с разными уровнями риска, вычислив отклонение для каждой из этих категорий.
| Степень риска | Стандартные отклонения |
| Очень низкий | 2,7 |
| Низкий риск | 3,58 |
| Средний риск | 4,18 |
| Высокий риск | 4,54 |
| Очень высокий | 6,62 |
Далее запишем, как находятся основные показатели относительного рассеивания.
Вопрос 2. Показатели относительного рассеивания
Коэффициент осцилляции К0 отражает относительные колебания крайних значений признака вокруг средней:
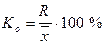 .
.
Относительное линейное отклонение Kd характеризует долю усреднённого значения абсолютных отклонений от средней величины.
 .
.
Коэффициент вариации u определяют по формуле:
 .
.
Коэффициент вариации измеряет рассеивание данных относительно среднего значения. Измеряется в %, а не в единицах измерения исходных данных.
Применение понятий
Коэффициент вариации доходности фондов с разными уровнями риска имеет следующие значения:
| Степень риска | Среднее | Стандартное отклонение | Коэффициент вариации, % |
| Очень низкий | 13,45 | 2,7 | 20,07 |
| Низкий риск | 12,23 | 3,58 | 29,29 |
| Средний риск | 11,21 | 4,18 | 37,28 |
| Высокий риск | 9,55 | 4,54 | 47,58 |
| Очень высокий | 6,08 | 6,62 | 108,88 |
Чем выше риск, тем больше относительный разброс доходности вокруг среднего значения. Фонды с низким и средним уровнями риска имеют более высокую среднюю доходность и меньший коэффициент вариации, чем фонды с высоким уровнем риска. Это означает, что эффективность фондов со средним уровнем риска выше, чем эффективность фондов с высоким уровнем риска.
Коэффициент вариации позволяет сравнить две выборки, элементы которых выражаются в разных единицах измерения.
Когда относительные показатели вариации не превышают 35%, то принято считать, что полученные средние (серединные) характеристики достаточно надежно характеризуют совокупность по варьирующему признаку, когда относительные показатели вариации больше 35% - то ненадежно. В этом случае варианты ряда распределения существенно отличаются от средних характеристик.
Вопрос 3. Виды дисперсии
Виды дисперсии – это показатель изменения признака в совокупности.
Определим три вида дисперсии:
общую дисперсию  ,
,
межгрупповую дисперсию  ,
,
среднюю внутригрупповых дисперсий  .
.
Общая дисперсия характеризует вариацию признака, которая зависит от всех условий в данной совокупности.
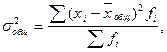
где  - общая средняя для всей изучаемой совокупности.
- общая средняя для всей изучаемой совокупности.
Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака фактора, положенного в основу группировки.
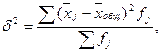
где  - средняя по отдельным группам;
- средняя по отдельным группам;
 - средняя общая;
- средняя общая;
 - численность отдельных групп.
- численность отдельных групп.
Средняя внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе. Это вариация результативного признака, которая возникает под влиянием всех остальных факторов, кроме группировочного.

где  - дисперсия в каждой группе.
- дисперсия в каждой группе.
Большую практическую значимость имеет правило сложения дисперсий:
 .
.
Коэффициент детерминации h2 находят по формуле:  .
.
Он характеризует долю вариации группировочного признака в общем объеме вариации или на сколько процентов уровень результативного признака определяется группировочным признаком.
Корень квадратный из коэффициента детерминации называется эмпирическим корреляционным отношением.
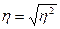
Это отношение характеризует тесноту связи между признаками, т.е. близость корреляционной (неполной) зависимости к функциональной (полной). Этот показатель изменяется от нуля до единицы. Точность его зависит от размеров совокупности: чем больше совокупность, тем он надежнее. Недостатки эмпирического корреляционного отношения: невозможность определить направление связи (прямая зависимость или обратная); невозможность определения формы связи.
Применение понятий
Распределение служащих двух отделов крупного предприятия по уровню зарплаты следующее:
| № | Уровень зарплаты, у.е. | Число служащих | ||
| отдел 1 | отдел 2 | Всего | ||
| 1. | до 100 | |||
| 2. | 100 - 105 | |||
| 3. | 105 - 110 | |||
| 4. | 110 - 115 | |||
| 5. |  115 115
| |||
| Итого |
Определить:
- среднюю зарплату по каждому отделу и предприятию в целом;
- дисперсию для каждого отдела;
- среднюю внутригрупповых дисперсий;
- межгрупповую дисперсию;
- общую дисперсию.
Решение:
Отдел 1.
 ,
,
 у.е.
у.е.
Отдел 2.
 у.е.
у.е.
Предприятие:
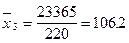 у.е.
у.е.
Дисперсию по каждому отделу определяем по формуле:
 ,
,
j = 1, 2
i = 1, 2, 3, 4, 5
 ,
,  . Аналогично для второго отдела.
. Аналогично для второго отдела.
Средняя внутригрупповая дисперсия:
 .
.
Межгрупповая дисперсия:
 .
.
Общая дисперсия:

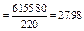 .
.
Проверка по правилу сложения дисперсий:
 .
.
Коэффициент (индекс) детерминации: 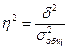 =0,75/27,98*100=2,7%.
=0,75/27,98*100=2,7%.
Вывод. Распределение служащих по отделам на 2,7% определяется уровнем заработной платы и на 97,3% всеми остальными факторами.
Эмпирическое корреляционное отношение будет равно:
 .
.
Вывод. Полученное значение свидетельствует о достаточно слабой связи между признаками, не приближающейся к функциональной зависимости.
Вопрос 4. Анализ данных. Базовые показатели. Блочные диаграммы.
Вычисление показателей с помощью Пакета Анализа
| Пятилетняя доходность фондов с высоким уровнем риска | |
| Среднее | 6,08 |
| Стандартная ошибка | 1,709084968 |
| Медиана | 6,5 |
| Мода | #Н/Д |
| Стандартное отклонение | 6,619257619 |
| Дисперсия выборки | 43,81457143 |
| Эксцесс | -0,224739779 |
| Асимметричность | -0,148297869 |
| Интервал | 24,6 |
| Минимум | -6,1 |
| Максимум | 18,5 |
| Сумма | 91,2 |
| Счет | |
| Наибольший(1) | 18,5 |
| Наименьший(1) | -6,1 |
Стандартная ошибка – стандартное отклонение деленное на квадратный корень объема выборки.
Ассиметричность характеризует отклонение от симметричности распределения и является функцией, зависящей от куба разностей между элементами выборки и средним значением.
Эксцесс – это мера относительной концентрации данных вокруг среднего значения по сравнению с хвостами распределения; зависит от разностей между элементами выборки и средним значением, возведенными в четвертую степень.
Основные характеристики позволяют описать свойства данных и перейти к более глубоким исследованиям. Довольно часто для анализа данных применяется подход, основанный на пятерке базовых показателей и построении блочной диаграммы.
Блочная диаграмма представляет собой удобное средство для изображения пяти базовых показателей:

Применение понятий

Здесь изображена блочная диаграмма, иллюстрирующая показатели среднегодовой доходности 15 фондов с очень высоким уровнем риска
Вертикальная линия, проведенная внутри прямоугольника, отмечает медиану. Левая сторона прямоугольника соответствует первому квартилю 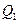 , а правая – третьему квартилю
, а правая – третьему квартилю  . Таким образом, прямоугольник содержит средние 50% элементов выборки. Младшие 25%данных изображаются в виде линии (так называемый ус), соединяющей левую сторону прямоугольника с наименьшим выборочным значением
. Таким образом, прямоугольник содержит средние 50% элементов выборки. Младшие 25%данных изображаются в виде линии (так называемый ус), соединяющей левую сторону прямоугольника с наименьшим выборочным значением  . Следовательно, старшим 25% данных соответствует линия, соединяющая правую сторону прямоугольника с наибольшим выборочным значением
. Следовательно, старшим 25% данных соответствует линия, соединяющая правую сторону прямоугольника с наибольшим выборочным значением 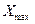 .
.
Изображение нескольких диаграмм на одном рисунке намного облегчает анализ и сравнение данных

Вывод: чем меньше риск, тем выше эффективность фондов
Вопрос 5. Дисперсия альтернативного (качественного признака)
Альтернативные – это признаки, которыми обладают одни единицы совокупности и не обладают другие.
Наличие изучаемого признака обозначается 1, а его отсутствие 0.
Доля показателей, обладающих изучаемым признаком, обозначается – р, а доля значений, не обладающих признаком, обозначается q.
P + q = 1
Найдем их средние значения и дисперсию.

 =
= 
Применение понятий
10 000 населения. Из них 4000 мужчин 6000 женщин
Р = 4000/10000 = 0,4 q = 6000/10000 = 0,6
 р*q = 0.4*0.6 = 0.24
р*q = 0.4*0.6 = 0.24
P + q не может быть больше 1, а р*q не может быть больше 0,25
Тогда 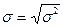 =
=  = 0,49.
= 0,49.
Дата добавления: 2015-07-12; просмотров: 575 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Абсолютные показатели вариации | | | Душа человека – сугубо индивидуальный феномен, который составляет и выражает собой уникальные особенности данной личности. |