Величина итогового показателя не должна изменяться при замене индивидуальных значений признака средней величиной.

Способность средних величин сохранять свойства статистических совокупностей называют определяющим свойством.

Средняя геометрическая применяется если при замене индивидуальных величин признака на среднюю надо сохранить неизменным произведение индивидуальных величин. Этот вид средней позволяет оценить степень изменения переменной с течением времени.

.

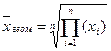Этой средней удобно пользоваться, если уделяется внимание отношениям двух чисел. Например, при расчётах среднегодовых темпов роста.

Средняя гармоническая - это величина, обратная средней арифметической. Она используется если по условиям задачи необходимо, чтобы неизменной оставалась при определении сумма величин, обратных индивидуальным значениям признака.

.

Средняя квадратическая применяется если при замене индивидуальных величин признака на среднюю величину надо сохранить неизменной сумму квадратов исходных величин. Основное применение при измерении вариации признака в совокупности.

.

Стаж, лет Хi	Х^2	1/Х
		1/3
		1/6

4< 4.25 < 4.5 < 4.75 – это свойство мажорантности средних. Чем больше показатель степени у Х_i , тем больше и величина соответствующей средней

Пример. Вопрос о том какой вид средней необходимо применить в отдельном случае, решается путем конкретного анализа изучаемой совокупности и исходных данных

Определить среднюю урожайность по хозяйству №1, по хозяйству №2 и по двум хозяйствам вместе

Зерновые культуры	хозяйство №1	хозяйство №2
Посевная площадь, га	Урожайность, ц с га	Валовой сбор, ц	Урожайность, ц с га
Рожь		20,9		21,8
Пшеница		25,1		26,3
Всего

₁= 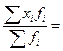9953/430=23,2ц с га – средняя арифметическая

₂= =9447/390=24,2ц с га – средняя гармоническая

_Σ=19400/820=23,7ц с га

Вопрос 2. Структурные средние величины.

Для характеристики структуры совокупности применяют структурные средние. К таким показателям относятся мода и медиана.

Мода - величина признака, которая встречается в изучаемом ряду, или в совокупности, чаще всего. Мода широко используется в коммерческой практике при изучении покупательского спроса, при регистрации цен и т.д. В дискретном ряду мода - это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант так называемого модального интервала, т.е. того интервала, который имеет наибольшую частоту:

где x_нmo - нижняя граница модального интервала;

i_mo - величина модального интервала;

f_mo - частота, соответствующая модальному интервалу;

f_mo-1, f_mo+1 - частоты интервалов, предшествующих и следующих за модальным интервалом.

Медиана - это величина, которая делит численность упорядоченного вариационного ряда на две равные части. Для упорядоченного дискретного ряда с нечетным числом значений – медиана – это серединный элемент ряда. Для упорядоченного дискретного ряда с четным числом значений – медиана – это среднее арифметическое двух серединных элементов ряда.

Для интервального ряда медианный - это интервал, для которого накопленная частота больше или равна полусуммы частот ряда. Для интервального ряда медиана находится по формуле:

где x_нme - нижняя граница медианного интервала;

i_me - величина медианного интервала;

S f/2 - полусумма частот ряда;

S_me-1 - сумма накопленных частот, предшествующих медианному интервалу;

f_me - частота медианного интервала.

Пример. Определить моду и медиану для заработной платы по следующим исходным данным:

№

Зарплата, у.е.

Численность

1.	90 - 100
2.	100 - 110
3.	110 - 120
4.	120 - 130
5.	130 - 140

Итого

у.е.

у.е.

Вывод. Наибольшее число работников имеет заработную плату равную 117 у.е.

50% работников имеют заработную плату свыше 117,3 у.е., а другие 50% - меньше 117,3 у.е.

Сумма абсолютных отклонений членов ряда от медианы есть величина наименьшая:

.

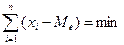Это особое свойство медианы находит широкое применение в маркетинговой деятельности.

Если среднее арифметическое значение, мода и медиана совпадают, то такая группа данных симметрична.

Величины, находящиеся на одной, двух и трёх четвертях расстояния от начала ряда называются квартилями, на одной десятой - децилями, на одной сотой - процентилями.

Пример. Вычислить значение медианы и трёх квартилей Q₁, Q₂, Q₃, для упорядоченных данных: 3, 5, 6, 7, 7, 8, 9, 11

Решение:

, ,

, .

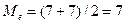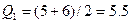Децилем называется структурная величина, которая делит распределение на 10 равных частей по 10% единиц или объемов в каждой части. Децилей девять, децильных групп – десять.

Пример. Распределение населения по уровню располагаемых ресурсов на 1 человека в семье (по материалам выборочного обследования)

Располагаемые ресурсы, тыс.руб.	Доля населения, % к итогу	Накопленные (интегральные) частоты
До 40	2,5	2,5
40-120	61.3	63,8
120-200	28,2
200-280	6,5	98,5
Свыше 280	1,5
всего

Определить децильный коэффициент дифференциации располагаемых доходов.

где к – номер дециля (для 1-го к=0,1; для 9-го к=0,9)

Определяем интервалы децилей (для 1-го 40-120; для 9-го 120-200)

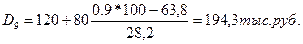
Тогда 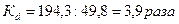, т.е. минимальный доход 10% богатых превышает максимальный доход бедных в 3,9 раза.

Дата добавления: 2015-07-12