Средние величины

Среди обобщающих показателей, характеризующих статистические совокупности, большое значение имеют средние величины.

Средняя величина — это обобщающая характеристика множества индивидуальных значений некоторого количественного признака.

Совокупность, изучаемая по количественному признаку, состоит из индивидуальных значений; на них оказывают влияние, как общие причины, так и индивидуальные условия. В среднем значении отклонения, характерные для индивидуальных значений, погашаются. Средняя, являясь функцией множества индивидуальных значений, представляет одним значением всю совокупность и отражает то общее, что присуще всем ее единицам.

В экономических исследованиях и плановых расчетах применяются две категории средних: степенные и структурные.

К степенным средним относятся: средняя арифметическая, средняя гармоническая, средняя геометрическая и средняя квадратическая. Выбор той или иной формы средней зависит от содержания усредняемого признака и конкретных данных, по которым ее приходится вычислять.

Средняя арифметическая – самый распространенный вид средней величины. Вычисляется, когда каждая варианта встречается в совокупности только один раз.

Введем обозначения: х_i – величины, для которых исчисляется средняя; - средняя, n – объем выборки (численность изучаемой совокупности). Тогда

.

Пример. Имеются данные о заработной плате десяти работников предприятия:

Профессия	Количество рабочих	Заработная плата (руб.)
Токари		1700, 1208, 1620, 917, 1400
Фрезеровщики		1810, 1550
Слесари		1210, 1380, 870

Вычислить среднюю месячную зарплату рабочих:

Средняя арифметическая взвешенная – используется, когда варианты повторяются различное число раз, при этом число повторений называется частотой или статистическим весом. Обозначим f_i - частота (вес), повторяемость индивидуальных значений признака, к – количество различных значений варианты в исследуемой совокупности.

.

Пример. Имеются данные о стаже рабочих на предприятии:

Стаж работы (хi)	До 5 лет	5-10 лет	10-15 лет	15 лет и более	Итого
Количество рабочих (fi)

Определить средний стаж рабочих.

В качестве значения варианты нужно взять середину указанного интервала по стажу работы, к = 4,

Следует отметить, что сумма всех весов равна объему выборки, то есть .

Средняя гармоническая взвешенная – вычисляется в тех случаях, когда статистическая информация не содержит частот по отдельным вариантам, а представлена как их произведение, то есть приходится суммировать не сами варианты, а их обратные величины.

.

Пример. Рассчитать среднюю сумму реализации товаров по имеющимся данным:

Город	Цена, руб. (xi)	Сумма реализации, тыс. руб. (fi)
А
Б
В

Расчет средней цены выражается отношением:

.

Для определения неизвестной величины – количества реализованных единиц – нужно отдельно по каждому городу разделить сумму реализации на цену. Поэтому при определении средней цены необходимо воспользоваться формулой средней гармонической взвешенной:

Средняя геометрическая - это величина, которая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин, как отношения каждого уровня ряда к предыдущему.

Пример. По имеющимся данным определить средний темп роста пенсий в России:

Год
Размер пенсии, руб./месяц (уровни ряда уi)		649,3

Рассчитаем средний темп роста по формуле средней геометрической:

Таким образом, в данном примере средний темп роста в год составил 137,97%.

К структурным средним относятся мода и медиана. Они соответствуют конкретным значениям признака совокупности, остальные значения на них не оказывают никакого влияния.

Важнейшей характеристикой центра распределения, кроме средней арифметической, является мода.

Мода - это значение признака, которое чаще всего встречается в вариационном ряду. Во многих случаях эта величина наиболее характерна для ряда распределения и вокруг нее концентрируется большая часть вариант. При изменении распределения в его концах мода не меняется, т.е. она обладает определенной устойчивостью к вариации признака. Поэтому моду наиболее удобно при­менять при изучении рядов с неопределенными границами.

Для дискретного ряда мода находится непосредственно по определению. Так, по данным таблицы, исходя из наибольшего значения частоты, определяем, что типичное число членов домашних хозяйств — 2 человека. Из 1000 домашних хозяйств 262 состоят всего из 2 человек (262 — максимальная частота ряда, а 2 — значе­ние признака, которое встречается чаще всего).

Число членов домашних хозяйств, чел. xi	Число домашних хозяйств fi	Накопленные частоты Si
5 и более
Итого

Для интервального ряда с равными интервалами сначала определяется модальный интервал [x_i,x_i+1] то есть интервал,которому соответствует максимальная частота f_k или частость w_k. Значение моды внутри модального интервала определяется по формуле:

,

где x₀ — нижняя граница модального интервала;

h — длина модального интервала;

f₁— частота интервала, предшествующего модальному,

f₂— частота модального интервала,

f₃— частота интервала, следующего за модальным.

Пример. Определим моду для данных о стаже рабочих. Модальным интервалом будет интервал [10;15], так как в него попало больше всего рабочих (15 человек). Для применения предложенной формулы найдем значения всех переменных, которые в ней используются: x₀ = 10; h = 5; f₁ = 6; f₂ = 15; f₃ = 7. Тогда мода будет равна:

.

То есть большинство из рассматриваемых работников имеет стаж 12,65 лет.

Графически моду определяют по гистограмме распределения (Рис. 3.). Для этого выбирают самый высокий прямоугольник, который и является модальным, далее верхнюю правую вершину модального прямоугольника соединяют с верхней правой вершиной предшествующего прямоугольника, а верхнюю левую вершину модального прямоугольника с верхней левой вершиной последующего прямоугольника. Абсцисса точки пересечения этих отрезков и будет модой распределения.

Рис. 3. Определение моды по гистограмме.

Медиана - такое значение признака, которое приходится на середину ранжированного ряда. Ранжированным называется ряд, варианты которого расположены в порядке возрастания. Таким образом, в ранжированном ряду распределения одна половина ряда имеет значения признака, превышающие медиану, другая — меньше медианы.

В дискретном ряду медиана находится непосредственно по определению на основе накопленных частот. Для распределения домашних хозяйств номер медианы 1000: 2 = 500. Накапливаем частоты до тех пор, пока не будет превзойден номер медианы. Так, 192 домашних хозяйства имеют не более одного члена, 192 + 262 = 454 домашних хозяйства — не более 2 членов, а 454 + 226 = 680 домашних хозяйств — не более 3 членов, т.е. 455-е, 456-е,..., 500-е и 501-е домашние хозяйства состоят из 3 человек. Таким образом, медиана данного ряда равна 3.

Ряд с четным числом членов делит пополам не одна, а две единицы совокупности. Так, в распределении объема выборки 50 в середине ряда расположены единицы совокупности под номерами 25 и 26.

Тогда . Однако на практике для простоты счета номер медианы при четном числе членов ряда определяется как . Номер медианы для ряда с нечетным числом членов равен .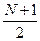

В случае интервального вариационного ряда сначала определяется медианный интервал. Для этой цели используются накопленные частоты. Медианным будет интервал, в котором накопленные частоты превзойдут номер медианы. Точное нахождение медианы на найденном интервале осуществляется по следующей формуле:

,

где x₀ — нижняя граница медианного интервала;

h — длина медианного интервала;

S_m-1 — накопленная частота интервала, предшествующего медианному;

f_m — частота медианного интервала.

Пример. Определим медиану для данных о стаже рабочих.

Стаж работы (хi)	До 5 лет	5-10 лет	10-15 лет	15 лет и более	Итого
Количество рабочих (fi)
Накопленная частота (Si)

Номер медианы 30: 2 = 15. Медианным интервалом будет интервал [10;15], так как в нем накопленные частоты (23) стали больше номера медианы. Для применения предложенной формулы найдем значения всех переменных, которые в ней используются: x₀ = 10; h = 5; S_m-1 = 8; f_m = 15. Тогда медиана будет равна:

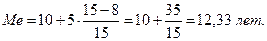
То есть половина из рассматриваемых рабочих имеет стаж менее 12,33 года, а половина – больше.

Из определения медианы следует, что она не зависит от тех значений признака, которые расположены по обе стороны от нее. В связи с этим медиана является лучшей характеристикой центральной тенденции в тех случаях, когда концы распределений расплывчаты (например, границы крайних интервалов открыты) или в ряду распределения имеются чрезмерно большие или малые значения.

Контрольные вопросы

1. Виды степенных средних и методы их расчета.

2. Структурные средние: мода и медиана.

3. Различия в расчете средних для дискретных и непрерывных данных.

Дата добавления: 2015-07-12