Источников тепла в изоляции и оболочках кабеля

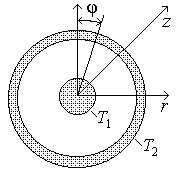Источником тепла является только жила кабеля (рис. 4.1). Процесс стационарный: .

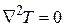В цилиндрической системе координат

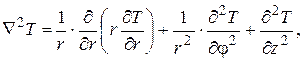(4.4)

где r – радиус; φ – угол; z – координата вдоль оси кабеля.

Рис. 4.1. Поперечный разрез кабеля

Вдоль оси кабеля температура не изменяется, поэтому производная равна нулю:

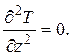(4.5)

По углу φ температура постоянная, поэтому производная равна нулю:

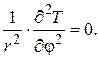(4.6)

С учетом (4.5) и (4.6) уравнение (4.4) примет вид

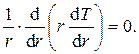(4.7)

или

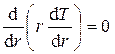(4.8)

Производная равна нулю в том случае, если дифференцируемая величина 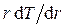является константой:

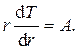(4.9)

Разделим переменные и проинтегрируем:

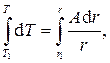
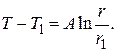(4.10)

Из выражения (4.10) находим A:

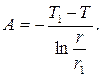(4.11)

На радиусе r = r ₂ температура T равна T ₂, следовательно:

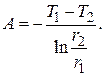(4.12)

Подставим (4.12) в (4.11), окончательно получим

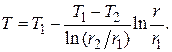(4.13)

Из формулы видно, что температура изменяется по логарифмическому закону.

Согласно закону Фурье, между тепловым потоком q и градиентом температуры существует линейная зависимость:

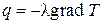или 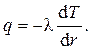(4.14)

Коэффициентом пропорциональности является теплопроводность l. Плотость теплового потока – это количество тепла Q, прошедшее через единицу поверхности S = 2p L в единицу времени t:

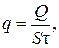
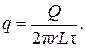(4.15)

Отношение количества тепла Q к времени t есть мощность P, т.е. P = Q /t, подставим ее в (4.15), получим

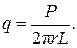(4.16)

Подставим (4.16) в (4.14) и разделим переменные:

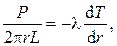
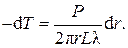
Интегрируем:

.

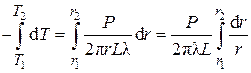Подставим пределы, получим

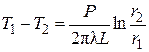или 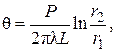(4.17)

где q = T ₁– T ₂ – перепад температур.

Обозначим через S тепловое сопротивление изоляции:

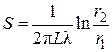или 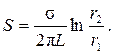(4.18)

где σ – удельное тепловое сопротивление (σ = 1/γ).

Подставим (4.18) в (4.17), получим тепловой закон Ома:

(4.19)

Согласно закону Джоуля – Ленца, выделяемая в проводнике при протекании тока мощность

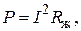(4.20)

где 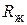– сопротивление проводника.

Подставим (4.20) в формулу (4.19) и выразим из нее ток:

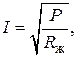
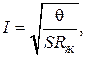
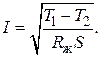(4.21)

Применительно ко всему кабелю формула (4.21) примет вид

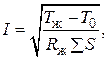(4.22)

где T _ж – температура жилы; T ₀ – температура окружающей среды; S S – сумма тепловых сопротивлений элементов конструкции кабеля и окружающей среды.

Дата добавления: 2015-07-12