При наличии диэлектрических потерь в изоляции

Рассмотрим случай, когда источниками тепла являются токопроводящая жила и изоляция. Жила разогревается за счет джоулевых потерь, изоляция – за счет диэлектрических потерь. Предварительно сделаем некоторые преобразования. Пусть мы имеем плоский конденсатор с однородным электрическим полем (рис. 4.2), мощность диэлектрических потерь в нем

(4.23)

Удельные диэлектрические потери (P _уд, Вт/м³), т.е. потери в единице объема изоляции

(4.24)

Рис. 4.2. Плоский конденсатор

В кабеле напряженность электрического поля изменяется по радиусу. Подставим формулу (2.15) в (4.24):

(4.25)

В элементарном объеме , ограниченном радиусами r и , диэлектрические потери (рис. 4.3)

(4.26)

Подставим в (4.25) формулу (4.26) и с учетом (4.23) получим

(4.27)

Рис. 4.3. Диэлектрические потери в элементарном объеме  

Мощность теплового потока от диэлектрических потерь, проходящего через слой с радиусом r

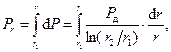
(4.28)

Тепловое сопротивление d S элементарного слоя толщиной пропорционально удельному тепловому сопротивлению s_из, и обратно пропорционально площади цилиндра S = 2π rL (примем длину L равной единице):

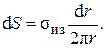(4.29)

В слое толщиной перепад температур

(4.30)

Подставим (4.28) и (4.29) в (4.30):

(4.31)

Между жилой и оболочкой разность температур

(4.32)

После интегрирования имеем

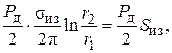
где

Окончательно

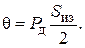(4.33)

В результате вывода мы получили, что распределенный источник тепла можно заменить сосредоточенным, расположенным на половине теплового сопротивления изоляции (рис. 4.4).

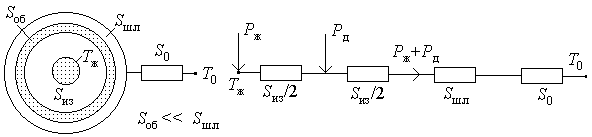
Рис. 4.4. Тепловая схема замещения кабеля с диэлектрическими потерями

Составим уравнение для тепловой схемы замещения (см. рис. 4.4), используя тепловой закон Ома:

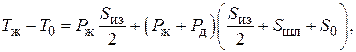
где S _из – тепловое сопротивление изоляции; S _шл – тепловое сопротивление шланга; S ₀ – тепловое сопротивление окружающей среды.

Сделаем преобразования

(4.34)

Тепловое сопротивление металлической оболочки не учитывается, так как тепловое сопротивление металла много меньше теплового сопротивления диэлектриков(S _об << S _шл). В токопроводящей жиле потери

(4.35)

Подставим (4.35) в (4.34) и выразим ток:

(4.36)

Дата добавления: 2015-07-12