Нагрев и охлаждение кабеля

При изменении тока нагрузки кабеля его температура будет изменяться во времени. Зависимость температуры от времени получится в результате решения дифференциального уравнения (см. формулу (4.1)).

Рассмотрим упрощенный расчет. Предположим, что кабель является однородным цилиндром. Обозначим количество тепла, которое:

– выделилось в жиле от протекания тока, Q;

– пошло на нагрев кабеля, Q ₁;

– рассеялось в окружающую среду, Q ₂.

Составим уравнение теплового баланса:

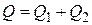. (4.60)

За бесконечно малый промежуток времени d t уравнение теплового баланса (4.60) примет вид

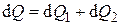, (4.61)

где

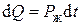, (4.62)

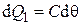, (4.63)

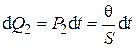, (4.64)

P _ж – мощность теплового потока, идущего от жилы; C – теплоемкость кабеля; P ₂ – мощность теплового потока, идущего от кабеля в окружающую среду; S – тепловое сопротивление; θ – перепад температур.

Подставим перечисленные величины в уравнение (4.61), получим

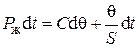; (4.65)

Разделим переменные:

; ;

; .

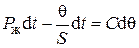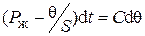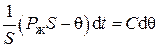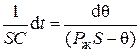Интегрируем по времени от 0 до t и по перепаду температур от 0 до θ:

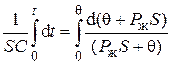. (4.66)

После интегрирования получим

.

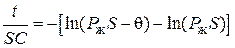Преобразуем эту формулу:

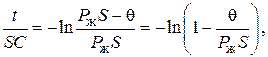
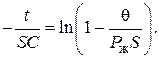
Потенцируем последнее выражение:

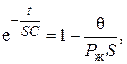
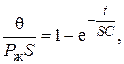
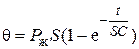, (4.67)

где .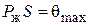

Окончательно имеем

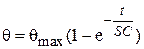или 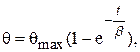(4.68)

где β – постоянная времени нагрева, β = CS.

Кабель охлаждается по уравнению

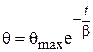(4.69)

При выводе этого уравнения мы принимали кабель за однородный цилиндр. Реальный кабель многослойный, и чтобы учесть это, вводится понятие эффективной теплоемкости

C = С _эф = С _ж + 0,5(С _из + С _об +...), (4.70)

где С _ж – теплоемкость токопроводящей жилы; С _из – теплоемкость изоляции; С _об– теплоемкость оболочки. Теплоемкость земли(С _з = 0)не учитывается, земля вокруг кабеля прогревается в течение нескольких недель.

Тепловое сопротивление берется с учетом теплового сопротивления земли:

S = S _из + S _об +…+ S _з. (4.71)

Тепловое сопротивление любого i -го цилиндрического элемента конструкции кабеля (S _из, S _об и т. д.) вычисляется по формуле (см. (4.18))

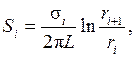(4.72)

где σ _i – удельное тепловое сопротивление, м·ºС/Вт; r _i, r_{i+ 1} – меньший и больший радиусы цилиндра; L – длина цилиндра (L = 1 м).

Теплоемкость любого i -го цилиндрического элемента конструкции кабеля вычисляется по формуле

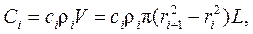(4.73)

где V – объем, м³; c_i – удельная теплоемкость, Дж/(кг·ºС); ρ _i – плотность, кг/м³.

Для токопроводящей жилы формула (4.73) примет вид

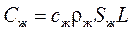, (4.74)

где 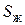– сечение жилы (по металлу), м².

Постоянная времени нагрева показывает время, за которое температура кабеля изменится в е раз от первоначального значения. Температура кабеля стабилизируется через (3–5)b, что составляет несколько часов.

Распишем уравнение (4.68):

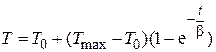, (4.75)

где T ₀ – температура окружающей среды; (T _max – T ₀) = θ – максимальный перепад температур; T – текущая температура.

Уравнение (4.75) представляет собой экспоненту (рис. 4.8), которая изменяется от температуры окружающей среды (T ₀) до максимальный температуры (T _max) с постоянной времени b.

Существует два способа определения постоянной времени нагрева b.

Первый способ – метод двух третей. В уравнение (4.68) подставим t = =b:

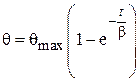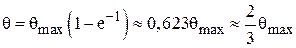; . (4.76)

За время, равное b, температура кабеля повышается на 2/3 от максимальной температуры (см. рис. 4.8).

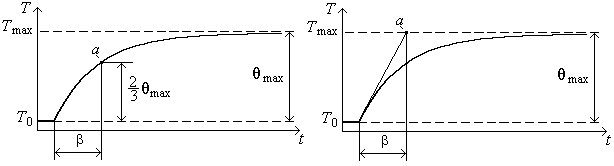
а б

Рис. 4.8. Определение постоянной времени нагрева: а – методом двух третей;

б – методом касательной

Второй способ – метод касательной. Продифференцируем уравнение (4.68) по времени:

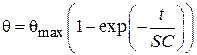или 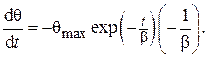(4.77)

Для исключения множителя 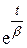подставим t = 0, тогда

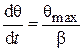. (4.78)

Производная 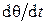– это есть не что иное, как касательная, проведенная к кривой нагрева в момент времени t = 0 (рис. 4.9, б). Этот метод менее точен из-за сложности проведения касательной.

Дата добавления: 2015-07-12