Наборы гексаграмм

Гексаграммы также имеют канонизированные порядки расположения, связанные с именами Фуси и Вэнь-вана. В первом случае порядок гексаграмм образуется при комбинировании в составе гексаграмм верхних и нижних триграмм, располагающихся в порядке Фуси. Существуют табличная, или “квадратная” (фан ту фан вэй), и круговая (юань ту фан вэй) записи этого порядка гексаграмм. Квадратная запись достаточно наглядно отражает принцип комбинирования триграмм (рис. 1.2.16).

Рис. 1.2.16

При круговой записи, которая подобна круговому расположению триграмм в порядке Фуси, первая половина всего набора гексаграмм располагается на круге против часовой стрелки, а вторая — по часовой стрелке.

В случае гексаграммного порядка Вэнь-вана, имеющего также табличную (рис. 1.2.17) и круговую записи, общую закономерность расположения гексаграмм синологам пока найти не удалось, хотя и совершалось немало попыток. Ничего общего с триграммным круговым порядком Вэнь-вана этот порядок не имеет, за исключением того, что оба приведены в “Чжоу и”. Именно в порядке под этим названием гексаграммы располагаются в основной части данного текста. Единственный и достаточно очевидный принцип связи гексаграмм, обнаруженный пока в этом порядке, заключается в том, что они группируются в пары по принципу переворачивания (фань), а там, где переворачивание приводит к исходной гексаграмме, — по принципу дополнительности (дуй).

Рис. 1.2.17

При археологических раскопках, проводившихся в 1973 г. в местечке Мавандуй (рядом с г. Чанша в пров. Хунань), был обнаружен самый древний экземпляр “Книги перемен”, датируемый 180—170 гг. до н.э. (см.: Вэнь у 1984: 1—8). В этом тексте гексаграммы располагаются в порядке, который у синологов получил название “мавандуйский” (рис. 1.2.18).

Рис. 1.2.18

Алгоритм данного порядка достаточно прост. Весь набор гексаграмм подразделяется на восемь серий, в которых имеются одинаковые верхние триграммы. Последовательность смены серий с данными триграммами соответствует их ранжированию по “семейным” характеристикам: отец, младший, средний и старший сыновья, мать, младшая, средняя и старшая дочери. Последовательность нижних триграмм построена по принципу дополнительности, совмещаемому со старшинством: отец и мать, младшие, средние и старшие сыновья и дочери (рис. 1.2.19).

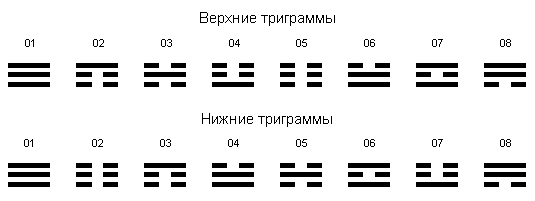
Рис. 1.2.19

Сочетания верхних и нижних триграмм в данных последовательностях приводят к образованию восьми серий гексаграмм, в которых затем осуществляется перестановка определенных гексаграмм в начало серии. Для перестановки берутся “чистые” (чунь) гексаграммы, т.е. составленные из одинаковых триграмм и имеющие их названия. В первой серии данная перестановка не требуется или может считаться чисто номинальной, поскольку в ее начале стоит как раз такая гексаграмма.

Еще один способ группировки гексаграмм — по “дворцам” — зафиксирован в сочинении раннеханьского ицзиниста Цзин Фана (77—33) “Цзин-ши и чжуань” (“Комментарий г-на Цзина к [Книге] перемен”). В основе построения системы “дворцов” лежит принцип поочередного изменения черт в позициях. Каждый дворец задается “чистой” гексаграммой. Поскольку таких гексаграмм восемь, то и дворцов тоже восемь (рис. 1.2.20).

Рис. 1.2.20

В каждом “дворце” каждая из пяти гексаграмм, находящихся после “чистой”, отличается от предыдущей только одной чертой, причем изменение черт происходит снизу вверх. Последняя в этом списке гексаграмма совпадает с “чистой” только верхней чертой. Ее изменение привело бы к переходу в другой дворец. Такими сцепленными дворцами, охватывающими в сумме 48 гексаграмм, являются дворцы Цянь и Кунь, Дуй и Гэнь, Ли и Кань, Чжэнь и Сюнь. В них в соответствующих местах стоят инвертные гексаграммы.

Оставшиеся 16 гексаграмм не подчиняются указанным закономерностям. Эти гексаграммы невозможно связать между собой посредством последовательного изменения одной черты. К первым шести гексаграммам в каждом дворце они подстраиваются за счет смены одной черты, но при этом нарушается предыдущий порядок переходов от позиции к позиции. При переходе в каждом дворце от шестой к седьмой гексаграмме изменяется четвертая снизу черта. Восьмые гексаграммы отличаются от первых пятой позицией. Между седьмой и восьмой гексаграммами различие образуется за счет инвертирования нижней триграммы.

Седьмые и восьмые гексаграммы в каждом дворце имеют особые названия. Они называются соответственно гексаграммами “странствующей души” (ю хунь) и “возвращающими душу” (гуй хунь). Как указывает Чжоу Цзунхуа, когда эти гексаграммы выпадают при гадании, это считается плохим предзнаменованием (Чжоу Цзунхуа 1996: 118). Судя по названиям и сопутствующим текстам, половина из них имеет положительные, а другая половина — отрицательные значения. Поэтому следует сделать уточнение. Негативный смысл все они, вероятно, приобретают в определенных случаях гадания, когда получаются две гексаграммы за счет изменения “подвижных” (бянь) черт. Исходная гексаграмма называется гуй хунь, если у нее изменяется только пятая черта, что приводит к образованию “чистой” гексаграммы. Если первая — гуй хунь, а вторая образуется за счет инверсии нижней триграммы, то она оказывается ю хунь.

Дата добавления: 2015-07-12