Читайте также:
|
Последовательное соединение - это совокупность связанных элементов электрической цепи, не имеющая узлов.
Отсюда следует, что по всем элементам последовательного соединения протекает одинаковый ток, т.к. изменение тока может происходить только в узлах электрической цепи.
В последовательное соединение в общем случае может входить любое количество резисторов и источников ЭДС (рис. 1), но не может входить более одного источника тока, т.к. это противоречило бы свойству каждого из источников создавать в цепи ток не зависящий от внешних элементов.
Падение напряжения между точками a и b рис. 1 можно представить разностью потенциалов этих точек Uab = j a - j b. Формально в эту разность можно включить произвольное число значений потенциалов (например, потенциалов точек соединения элементов) с противоположными знаками, а затем попарно объединить их -
| Uab = j a - j b = j a -j с +j с -j d +j d -...-j i +j i -j k +j k -... -j q +j q - j b = = (j a -j с)+(j с -j d)+(j d -...-j i)+(j i -j k)+(j k -... -j q)+(j q - j b) = = Uac + Ucd + Ude +...+ Uik + Ukl + Ulm +...+ Uqb = = Ir 1+ Ir 2+ Ir 3+...+ Irm + E 1+ E 2+...- En = = I (r 1+ r 2+ r 3+...+ rm)+(E 1+ E 2+...- En) = IR + E | (1) |
Таким образом, любое последовательное соединение можно преобразовать к последовательному соединению одного эквивалентного резистора и одного источника ЭДС. Причем, сопротивление эквивалентного резистора равно сумме всех сопротивлений входящих в соединение, а ЭДС эквивалентного источника равна алгебраической сумме ЭДС источников входящих в соединение.
Последовательное соединение элементов обладает свойством коммутативности, т.е. любые элементы этого соединения могут произвольно переставляться в пределах соединения. Это свойство непосредственно следует из коммутативности слагаемых выражений (1).
Так как эквивалентное сопротивление R представляет собой сумму положительных слагаемых, то R > rmax, где rmax - наибольшее из сопротивлений, входящих в соединение.
Если последовательное соединение подключено к узлам электрической цепи, то его определение тождественно определению ветви, следовательно, ветвь может быть образована только последовательным соединением.
ЗАДАЧА 1
В отличие от последовательного соединения, в параллельном следует различать параллельное соединение элементов цепи и параллельное соединение ветвей.
Параллельное соединение элементов - это совокупность элементов электрической цепи, объединенных двумя узлами и не имеющих связей с другими узлами.
В параллельное соединение элементов в общем случае могут входить резисторы и
источники тока (рис. 2), но не может входить более одного источника ЭДС, т.к. это противоречило бы их свойству создавать на выходе разность потенциалов не зависящую от внешней цепи.
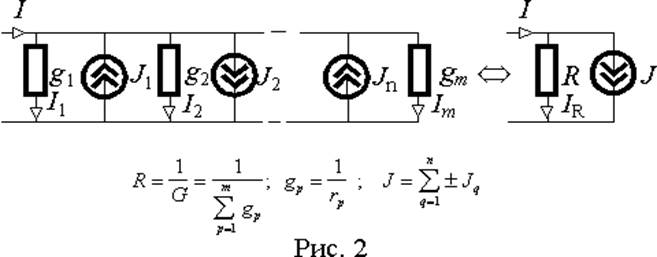Все элементы в параллельном соединении подключены к двум узлам и падение напряжения между этими узлами одинаково для всех элементов.
Общий ток, протекающий через параллельное соединение I можно представить суммой токов в отдельных элементах в виде I = I 1+ I 2+...+ In - J 1+ J 2+...+ Jm. Отсюда, раскрывая токи через сопротивления через напряжение между узлами U, получим
| I = Ug 1+ Ug 2+...+ Ugn - J 1+ J 2+...+ Jm = = U (g 1+ g 2+...+ gn) -(J 1+ J 2+...+ Jm)= UG + J | (2) |
Таким образом, параллельное соединение любого количества элементов можно преобразовать к параллельному соединению одного эквивалентного резистора и одного источника тока. Причем, сопротивление эквивалентного резистора равно величине обратной сумме всех проводимостей резисторов входящих в соединение, а ток эквивалентного источника равен алгебраической сумме токов источников входящих в соединение.
Аналогично последовательному соединению, параллельное обладает свойством коммутативности, вытекающим из свойства коммутативности сумм выражений (2).
При параллельном соединении для эквивалентной проводимости G, являющейся суммой проводимостей отдельных элементов, справедливо отношение G > gmax, где gmax - наибольшая из проводимостей элементов, образующих соединение. Отсюда G =1/ R > gmax =1/ rmin Þ R < rmin, т.е. эквивалентное сопротивление резисторов, входящих в параллельное соединение меньше наименьшего из них rmin.
Понятие сопротивления более привычно и употребимо, чем эквивалентное ему понятие проводимости. Поэтому при параллельном соединении приходится решать задачу определения именно эквивалентного сопротивления. Для двух, трех и четырех соединенных параллельно резисторов эквивалентные сопротивления R приведены в таблице 1. Для большего числа сопротивлений нетрудно получить аналогичные выражения из соотношений, приведенных на рис. 2.
Таблица 1.
| r 1; r 2 | r 1; r 2; r 3 | r 1; r 2; r 3 ; r 4 | |
| R = | 
| 
| 
|
ЗАДАЧА 2
В параллельное соединение могут входить не только элементы, но и ветви, каждая из которых может быть последовательным соединением элементов (рис. 3 а)). В этом случае используется понятие параллельного соединения ветвей, под которым понимают совокупность ветвей электрической цепи, объединенных двумя узлами и не имеющих связей с другими узлами.
На рис. 3 а) ветви R1R2 и R3 соединены параллельно, но элементы R1R3 и R2R3 параллельного соединения не образуют, т.к. эти пары элементов не объединены двумя узлами. Очевидно, что для них не выполняется и условие равенства падений напряжения.
ЗАДАЧА 3
Схемы цепей рис. 3 относят обычно к смешанному соединению, понимая под ним совокупность последовательного и параллельного соединений элементов и ветвей цепи.
Можно показать, что любую электрическую цепь путем поэтапных преобразований соединений элементов можно привести к последовательному соединению R-E или эквивалентному параллельному соединению G - J. Этот метод позволяет решать довольно сложные задачи и особенно эффективен, если требуется определить режим в какой-либо отдельной ветви цепи. Пример таких преобразований приведен на рис. 4.
Здесь на отдельных этапах преобразования параметры элементов определяются из выражений: R 34= R 3+ R 4; J 2= E 2/ R 2; R 234=(R 2 R 34)/(R 2+ R 34); J ' = J + J 2; E ' = J ' R 234; R = R 1+ R 234; E = E ' - E 1; J = E / R.
Особая задача, связанная с преобразованием цепей, состоит в определении сопротивления ( входного сопротивления ) цепи относительно точек разрыва. Она возникает, в частности, при использовании метода эквивалентного генератора для анализа электрических цепей в статических режимах, а также при составлении характеристического уравнения для анализа переходных процессов. Можно показать, что эквивалентное сопротивление R на рис. 4, является входным сопротивлением этой цепи и может быть определено по описанной ниже методике.
Собственно, методика заключается в том, что до начала эквивалентных преобразований в цепи нужно заменить все источники ЭДС и тока их эквивалентными сопротивлениями, а затем определить эквивалентное сопротивление. Как известно, сопротивление источника ЭДС равно нулю, а сопротивление источника тока - бесконечности. Поэтому на электрической схеме источники ЭДС нужно заменить связью, а источники тока - разрывом цепи. Рассмотрим этот процесс на примере рис. 5, где точка разрыва цепи, относительно которой нужно определить входное сопротивление, помечена крестиком.
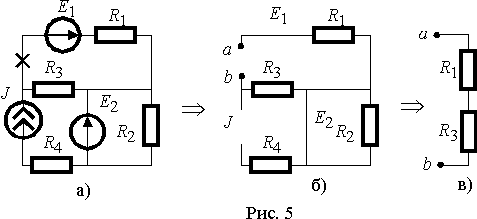
Вначале заменим источники их эквивалентными сопротивлениями и изобразим разрыв в явном виде точками a и b (рис. 5 б)). Теперь задача становится очевидной, т.к. цепь от точки a к точке b представляет собой последовательное соединение R 1 и R 3.
ЗАДАЧА 4
Дата добавления: 2015-07-12; просмотров: 249 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Источники электрической энергии | | | Последовательное соединение элементов электрических цепей |