
|
Читайте также: |
Источники электрической энергии являются необходимым элементом любой электрической цепи.
Их разделяют на идеальные и реальные источники. В свою очередь, идеальные источники делятся на источники электродвижущей силы (ЭДС) и источники тока.
Источники ЭДС - это такие элементы электрической цепи, у которых разность потенциалов на выходе не зависит от величины и направления протекания тока, т.е. их вольтамперные характеристики (ВАХ) представляют собой прямые линии параллельные оси I (см. таблицу 2).
Направление стрелки в условном обозначении источника ЭДС указывает направление действия ЭДС, поэтому направление падения напряжения на выходных зажимах источника всегда противоположно.
Так как на ВАХ электрическое сопротивление соответствует котангенсу угла наклона характеристики, то сопротивление источника ЭДС равно нулю, а проводимость, соответственно, бесконечности.
Источники тока - это такие элементы электрической цепи, у которых протекающий через них ток не зависит от знака и значения разности потенциалов на выходе, т.е. их (ВАХ) представляют собой прямые линии параллельные оси U (см. таблицу 2).
Отсюда, сопротивление источника тока равно бесконечности, а проводимость - нулю.
Направление стрелки в условном обозначении источника тока указывает направление протекания тока.
Источники ЭДС и источники тока часто рассматриваются как некие абстракции, не имеющие реального физического воплощения. Однако, это справедливо только, если считать, что их ВАХ не имеют ограничения. В этом случае ток через источник ЭДС или падение напряжения на источнике тока могут достигать бесконечно больших значений. При этом мощность источника (P = U×I) должна быть бесконечно большой, что исключает возможность технической реализации.
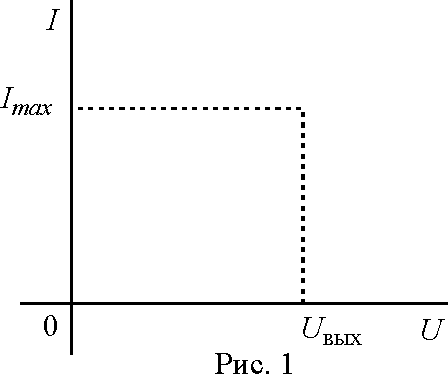 Если же ток и/или напряжение источника ограничено, то свойствами идеального источника обладают, например, стабилизированные источники питания, типичная ВАХ которых приведена на рис. 1
Если же ток и/или напряжение источника ограничено, то свойствами идеального источника обладают, например, стабилизированные источники питания, типичная ВАХ которых приведена на рис. 1
Выходное напряжение такого устройства U вых постоянно до тех пор, пока ток нагрузки не достигнет максимально допустимого значения Imax, после чего источник питания из режима стабилизации напряжения переходит в режим стабилизации тока. В пределах обоих режимов источник питания обладает свойствами соответственно идеального источника ЭДС и источника тока.
Идеальные источники ЭДС и тока используются также для моделирования некоторых электромагнитных процессов и нелинейных элементов электрических цепей, таких, например, как диод.
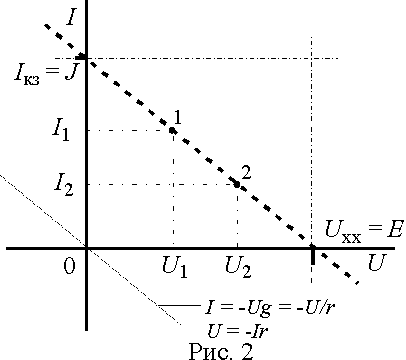 Реальные источники электрической энергии (ИЭ) имеют ВАХ, показанную на рис. 2.
Реальные источники электрической энергии (ИЭ) имеют ВАХ, показанную на рис. 2.
ВАХ реальных источников пересекает обе оси координат и эти точки пересечения соответствуют нулевому току через источник и нулевому падению напряжения. Режим с нулевыи током и ненулевым падением напряжения называется холостым ходом, а режим с нулевым падением напряжения и ненулевым током на выходе - коротким замыканием.
Уравнение ВАХ ИЭ представляет собой уравнение прямой линии в координатах U - I. Его можно получить из уравнения прямой линии, проходящей через начало координат I = - Ug = - U / r либо из обратной функции U = - Ir, где r - коэффициент соответствующий котангенсу угла наклона к оси U и имеющий размерность сопротивления, а g = 1/ r - тангенс угла наклона с размерностью проводиомсти. Для получения ВАХ ИЭ можно сместить линию I = - Ug на величину тока короткого замыкания
| I = - Ug + I кз = I кз - Ug = J - Ug | (1) |
или обратную функцию U = - Ir сместить на величину напряжения холостого хода.
| U = - Ir + U хх = U хх - Ir = E - Ir | (2) |
В выражениях (1) и (2) ток короткого замыкания I кз и напряжение холостого хода U хх являются константами, поэтому их можно заменить равным по значению током J и ЭДС E соответствующих идеальных источников, т.к. параметры идеальных источников также являются константами. Тогда выражениям (1) и (2) можно поставить в соответствие электрические схемы рис. 3 а) и б).
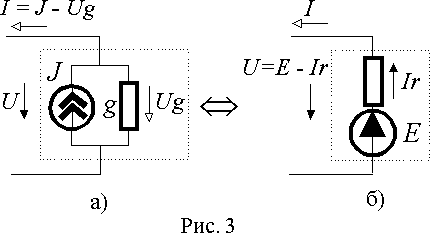
Выражения (1) и (2) и соответствующие им схемы рис. 3 описывают один и тот же элемент электрической цепи, имеющий ВАХ, представленную на рис. 2. Поэтому оба варианта совершенно эквивалентны и могут применяться в зависимости от целей и удобства конкретного представления.
В ИЭ сопротивление r и проводимость g называются соответственно внутренним сопротивлением и внутренней проводимостью источника.
Из выражений (1) и (2) следует, что ток I на выходе ИЭ отличается от значения тока внутреннего источника J на величину тока Ug, ответвляющегося внутри ИЭ через проводимость g. Аналогично, напряжение U на выходе источника отличается от значения ЭДС внутреннего источника на величину падения напряжения Ir на внутреннем сопротивлении r. Поэтому, чем меньше внутреннее сопротивление ИЭ r, тем ближе его свойства к свойствам идеального источника.
При r® 0 ИЭ становится источником ЭДС, однако, в эквивалентной схеме с источником тока g = 1/ r® ¥, и J = E / r ® ¥. Отсюда следует, что при преобразовании источника ЭДС с конечными значениями параметров мы получим ИЭ с бесконечным значением тока. Идентичные рассуждения можно привести и для преобразования ИЭ с источником тока при g® 0.
Таким образом, любой реальный источник электрической энергии, представленный, например, схемой а) рис. 3 можно преобразовать и представить эквивалентной схемой рис. 3 б) и наоборот. В то же время, идеальные источники (источники ЭДС и тока) в принципе не могут быть преобразованы один в другой.
ЗАДАЧА 1
Параметры ИЭ в схемах а) и б) связаны между собой следующими соотношениями:
E = Jg; r = 1/ g; J = E / r; g = 1/ r
ЗАДАЧА 2
На практике параметры ИЭ определяют по координатам двух точек ВАХ, т.е. по значениям тока и падения напряжения на выходе источника в двух произвольных режимах (при любых двух значениях сопротивления нагрузки, подключенного к выходным зажимам ИЭ).
Пусть измерены значения токов и падений напряжения в нагрузке в режиме 1 и 2 рис 2. Тогда по этим параметрам можно определить параметры схем рис. 3 следующим образом:
 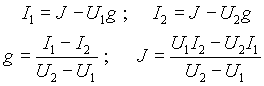 для схемы а) или для схемы а) или
| (3) |
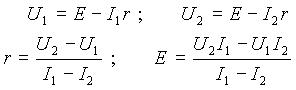 для схемы б). для схемы б).
| (4) |
ЗАДАЧА 3
Выражения (3) и (4) позволяют определить искомые параметры источников в общем случае, однако задачу можно существенно упростить, если источник допускает режимы холостого хода и/или короткого замыкания. Тогда достаточно измерить:
Для этих трех случаев выражения (3) и(4) преобразуются с учетом того, что I хх =0, и U кз =0, к виду представленному в таблице 1:
Таблица 1.
| Схема замещ. | Исходные параметры | ||
| U хх, U, I | I кз, U, I | U хх, I кз | |
| Рис. 3 а) | J = U хх I /(U хх - U) g = I /(U хх - U) | J = I кз g = (I кз - I)/ U | J = I кз g = I кз/ U хх |
| Рис. 3 б) | E = U хх r = (U хх - U)/ I | E = I кз U /(I кз - I) g = (I кз - I)/ U | E = U хх r = U хх / I кз |
ЗАДАЧА 4
На практике параметры ИЭ можно определить также с помощью переменной нагрузки без одновременного измерения тока и напряжения. Для этого достаточно, например, измерить напряжение холостого хода U хх, а затем подключить и изменять нагрузку до тех пор, пока падение напряжения на ней не станет равным U хх/2. Можно также измерить ток короткого замыкания I кз, а затем подключить и изменять нагрузку до тех пор, пока ток в ней не станет равным I кз/2. В обоих случаях внутреннее сопротивление источника r будет равно сопротивлению нагрузки R н.
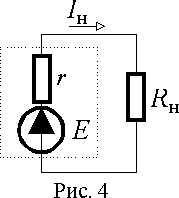 Рассмотрим подробнее этот способ для случая ИЭ с источником ЭДС показанного на рис. 4. При подключении нагрузки R н напряжение на выходе источника уменьшается в два раза, т.е. U хх = E =2 U н. В то же время, U н = E - Ir. Отсюда внутреннее сопротивление
Рассмотрим подробнее этот способ для случая ИЭ с источником ЭДС показанного на рис. 4. При подключении нагрузки R н напряжение на выходе источника уменьшается в два раза, т.е. U хх = E =2 U н. В то же время, U н = E - Ir. Отсюда внутреннее сопротивление
r = (E - U н)/ I = (2 U н - Uн)/ I = U н / I = R н.
Аналогично для схемы ИЭ с источником тока после подключения нагрузки ток во внешней цепи уменьшится вдвое, т.е. I кз = J =2 I н и I н = J - Ug. Тогда
g = (J - I н)/ U = (2 I н - Iн)/ U = I н / U = G н
Таким образом, если в нагрузке протекает ток равный половине значения тока короткого замыкания источника или падение напряжения на ней составляет половину от напряжения холостого хода, то в таком режиме сопротивление нагрузки и ее проводимость в точности равны внутреннему сопротивлению и проводимости ИЭ.
ЗАДАЧА 5
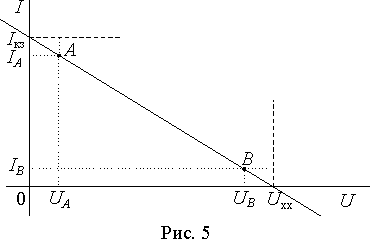 Реальные источники электрической энергии обладают внутренним сопротивлением, соответствующим потерям в самом источнике и теоретически не могут быть представленными без него. Однако на практике часто бывает целесообразным не учитывать внутреннее сопротивление. Оценим возникающую при этом погрешность.
Реальные источники электрической энергии обладают внутренним сопротивлением, соответствующим потерям в самом источнике и теоретически не могут быть представленными без него. Однако на практике часто бывает целесообразным не учитывать внутреннее сопротивление. Оценим возникающую при этом погрешность.
Пусть источник имеет вольтамперную характеристику, представленную на рис. 5, и пусть к нему поочередно подключаются две различные нагрузки, соответствующие работе источника в точках A и B. Причем нагрузки выбраны таким образом, что IB = I кз- IA =D I и UA = U хх- UB =D U, т.е. отклонение тока в точке A от тока короткого замыкания равно току в точке B, а отклонение напряжения в точке B от напряжения холостого хода равно напряжению в точке A.
Выразим отклонения тока и напряжения в относительных единицах, приняв за базовые значения напряжение холостого хода U хх и ток короткого замыкания источника I кз -
| D I = d I Iкз; D U = d U Uхх. | (5) |
Тогда напряжение и ток в нагрузке в точках A и B будут
| UA = d U Uхх; IA = I кз - d I Iкз = I кз(1 - d I); UB = U хх - d U Uхх = U хх(1 - d U); IB = d I Iкз. | (6) |
Но из подобия прямоугольных треугольников
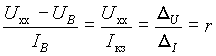 ,
,
где r - внутреннее сопротивление источника. В то же время из (5)
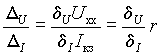 ,
,
следовательно d U = d I = d и из выражений (6)
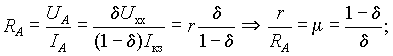
| (7) |
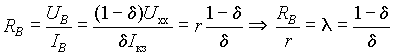 . .
| (8) |
 В выражении (7) m - отношение внутреннего сопротивления источника к сопротивлению нагрузки, а d - относительное отклонение тока нагрузки от тока короткого замыкания источника. В выражении (8) l - отношение сопротивления нагрузки к внутреннему сопротивлению источника, а d - относительное отклонение напряжения нагрузки от напряжения холостого хода источника.
В выражении (7) m - отношение внутреннего сопротивления источника к сопротивлению нагрузки, а d - относительное отклонение тока нагрузки от тока короткого замыкания источника. В выражении (8) l - отношение сопротивления нагрузки к внутреннему сопротивлению источника, а d - относительное отклонение напряжения нагрузки от напряжения холостого хода источника.
Таким образом, замена реального источника на источник тока или источник ЭДС приведет к появлению положительной погрешности d, величина которой зависит от отношения величин внутреннего сопротивления источника и сопротивления нагрузки (l = 1/m). При замене источником тока для оценки погрешности нужно брать отношение m, а при замене источником ЭДС - отношение l.
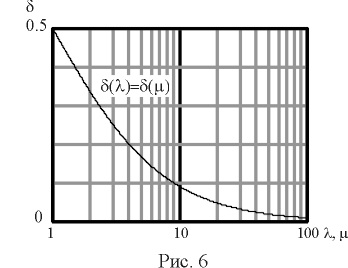
Зависимости d (l) и d (m) совершенно идентичны (рис. 6) и из них следует, что при R н > 20 r исключение внутреннего сопротивления источника и представление его источником ЭДС приведет к погрешности менее 5%. Такую же погрешность создаст замена реального источника на источник тока, если 20 R н < r.
Изложенные выше сведения по источникам электрической энергии кратко можно свести в таблицу
Таблица 2.
Дата добавления: 2015-07-12; просмотров: 120 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Топологические параметры цепи | | | Эквивалентные преобразования электрических цепей |