Общая структура электронно‑колебательных спектров поглощения; форма электронно‑колебательных полос поглощения.

Опыт показывает, что вращательная структура спектров поглощения наблюдается только в парах простых молекул, где имеет место свободное вращение. В растворах не наблюдается вращательных спектров. Отчетливо выраженные колебательные полосы наблюдаются только у двухатомных молекул. Для сложных молекул с числом ядер больше 3–4 разрешенных колебательных уровней не наблюдается, вместо этого имеют место широкие размазанные полосы. Это происходит из наложения колебаний из-за высокой плотности колебательных уровней и взаимодействия различных нормальных колебаний.

Рассмотрим качественно форму электронно-колебательных полос поглощения. Большое значение при анализе формы полосы поглощения имеет плотность колебательных уровней g(Eкол), т.е. число уровней на единичный интервал энергии. Оказывается, что плотность колебательной энергии увеличивается с ростом запаса колебательной энергии. Поясним это утверждение примером. Пусть у некоторой молекулы существуют две нормальные колебательные частоты: ν1=101 см‑1, ν2=130 см‑1. Рассмотрим плотность колебательных уровней в трёх равных интервалах энергии: ΔЕ1=0‑300 см‑1; ΔЕ2=1000–1300 см‑1; ΔЕ3=5000–5300 см‑1. Начало отсчета энергии расположено на уровне, соответствующем нулевым колебаниям.

Можно подсчитать, что в интервале ΔЕ1 плотность уровней g(E) составляет 50 см‑1, в ΔЕ2 — g(E)=10 см‑1, в ΔЕ3 — g(E)=2,5 см‑1. Таким образом, можно сказать, что с ростом запаса колебательной энергии возрастает. Поскольку запас колебательной энергии зависит от числа степеней свободы, в больших молекулах колебательные уровни энергии расположены очень близко, они сильно взаимодействуют друг с другом (частично за счет ангармонических членов в гамильтониане) и поэтому в электронно-колебательном спектре образуются полосы.

Обсудим на качественном уровне форму полосы поглощения сложных молекул. Пусть мы имеем два электронных уровня — основной, обозначаемый двумя штрихами, и возбужденный, обозначаемый одним штрихом, и соответствующие колебательные подуровни. Вероятность перехода с данной частотой ν B(ν) можно записать следующим образом (рис. 9):

(3.3.)

Из соотношения (3.2) следует, что переход будет тем вероятней, чем точнее будут расположены колебательные подуровни относительно электронных уровней, т.е. чем меньше будет величина |Екол-Е»кол| и следовательно B(x)@|Екол-Е»кол|‑1. Так, вероятность перехода с нижнего колебательного уровня основного состояния на колебательные подуровни возбужденного электронного уровня будет иметь вид:

Напомним, что в формуле (3.3) величина g(Е'кол)‑1 увеличивается с ростом запаса колебательной энергии. Поэтому вероятность перехода с частотой ν, полученная по формуле (3.3), будет иметь вид гладкой кривой с максимумом (рис. 10). Полная вероятность перехода может быть получена путем интегрирования выражения (3.3) с учетом плотности и заселенности колебательных состояний нижнего электронного уровня.

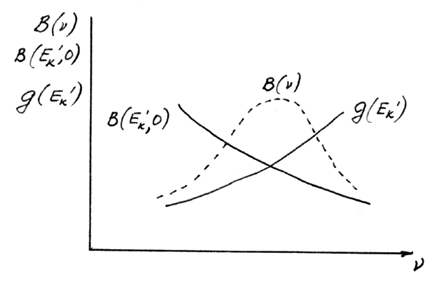Рис. 9

Рис. 10

(3.4)

В этом выражении:

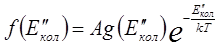
(3.5)

Окончательно для вероятности перехода мы имеем следующее выражение:

?

Из выражения (3.5) следует, что форма и положение полосы в спектре поглощения сложной молекулы зависит от многих факторов. Во-первых, от величины вероятности перехода между различными колебательными уровнями основного электронного состояния и франк-кондоновскими колебательными уровнями возбужденного состояния (это распределение А.Н.Теренин называет конфигурационным). Во-вторых, вероятность перехода согласно (3.5) зависит от определяемой температурой заселенности колебательных подуровней нижнего электронного состояния. Из приведенного качественного рассмотрения следует, что частота максимума в спектре поглощения сложной молекулы простого физического смысла не имеет; эта частота не совпадает с частотой 0 — 0 перехода.

Дата добавления: 2015-07-11