Оценивание параметров выбранной структуры.

В [Л: №3] не рекомендуется использовать структуру моделей (*) при n=2, если на графике переходной функции объекта h0(t) не просматривается характерный для S – образных кривых прямоугольный участок, а сама переходная кривая приближается к установившемуся значению:

сравнительно медленно пересекая вертикаль из точки В ниже значения:

в этом случае рекомендуется принимать значения:

Т01¹Т02

Рассмотрим некоторые методы оценки параметров дифференциальных уравнений в выбранной структуре по кривой разгона

1. Метод площадей (метод Симою)

В основе этого метода лежат следующие предположения

-

объект линейный с самовыравниванием:

- начальные условия нулевые:

(2), (3), (4)

Выражение (1) с учетом условия (3) запишется следующим образом:

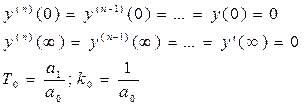Запишем уравнение (1) в следующем виде:

Возьмём интеграл от левой и правой части от 0 до ¥ и с учетом условий (2) и (3) получим:

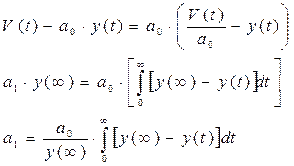Аналогично можно определить значение коэффициента а2, предварительно взяв интеграл от выражения (4) в пределах от 0 до ¥.

С учётом условий (2) и (3) получим:

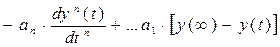К полученному выражению к левой и правой части применим операцию интегрирования от 0 до ¥.

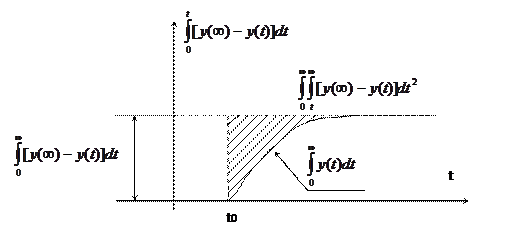
Если модель

Если модель объекта выбрана астатической, то есть в выражении (1) а0=0, тогда используя такую же схему можно записать следующее выражение:

tgg=y’(¥)

Таким образом, коэффициенты обеспечивают по видимому интегральный критерий аппроксимации, который обеспечивает приближение по всей кривой разгона. Эта схема является менее чувствительной к ошибкам регистрации кривой разгона, чем у метода касательной и с этой точки зрения является предпочтительной.

Рассмотрим вторую схему.

2.Модифицированный метод касательной.

Если n=2, то Т01=Т02

Т01=Т02=Т0/2,72

t’0=t0-0.107T0 или Т01/Т02=0,5

При этом постоянные времени Т01 и Т02 определяют следующим образом, по ординате h(t2)=0,63k0 экспериментальной переходной характеристике находят момент времени t2 отсчитываемый от точки D (то ест без учёта запаздывания), а затем вычисляют:

Т01=0,5Т02

Т0=0,64Т02

Такая аппроксимация целесообразна при условии:

h(0,5t2)³0,3k0

При n=1:

t’(0)»t0-0,11T0

T’0=0,64T0

В.А. Лукас ничего не говорит о критерии аппроксимации, поэтому можно предположить, что приближение осуществляется по всей кривой разгона. Так как в основу положен метод касательной, то по отношению к методу Симою способ Лукаса проигрывает в случае, если кривая разгона содержит погрешность.

3.Способ В.А. Маковского.

В отличие от предыдущих способов Маковский предлагает в качестве структуры модели преобразующих каналов для аппроксимации последовательное соединение интегрального звена с отсечкой и звена запаздывания.

Он предлагает инженерный слабо формализуемый способ определения параметров этой структуры.

В своей книге В.А. Маковский явно не указывает критерии аппроксимации, но по смыслу материала изложенного на стр. 223-226 [Л:] видно, что этим критерием является мера близости АФХ-ик объекта между действительной и расчетным годографом.

В точке перегиба проводится касательная, определяющая параметры Т0 и t0, при этом время запаздывания t0’ принимается равным интервалу времени, в течение которого выходная величина составляет 1-2% от Δy(¥). Из этой точки проводится прамая А до пересечения с линией установившегося состояния, таким образом, что эта прямая пересекает кривую разгона в трёх точках В, С, D, причём таким образом, чтобы площади S1 B S2, были примерно одинаковы.

Таким образом, построенная по этим методам запаздывающая наклонная функция имеет пять общих точек с экспериментальной кривой разгона (три точки – пересечения и равенство в областях начального и установившегося состояния). Здесь, в этой книге приведены формулы и монограммы для расчёта типовых регуляторов стр.227-233 в ориентации на то, что структура модели преобразующих каналов представляет собой последовательное соединение интегрального звена с отсечкой и звена запаздывания.

В [Л: №4] предлагается ещё один способ аппроксимации кривой разгона

стр. 344-351, когда структура модели представлена в виде (n+1)-го звена первого порядка и звена чистого запаздывания. В качестве критерия аппроксимации записываются следующие выражения:

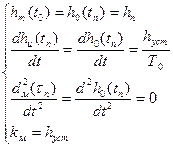
hм, h0 – соответственно модельная (расчётная) и опытная кривая разгона.

Индекс n указывает координаты точки перегиба.

hn – значение переходной характеристики в точке перегиба.

Т0 – значение постоянной времени, найденной методом касательной в точке перегиба.

В журнале “Теплоэнерготехника” №11,1995г. стр.75-80 приводится статья “Программы определения передаточных функций объектов управления по переходным характеристикам” где представлены алгоритмы и программы расчетов на PVM параметров передаточных функций переходных каналов по их передаточным характеристикам на языке QBASIK.

Дата добавления: 2015-07-11