Способы обработки кривых разгона.

В литературе по ТАР приведено достаточно много способов обработки кривых разгона, например:

1.Дудников Е.Г. Основы автоматического регулирования тепловых процессов. – Ленинград: Госэнергоиздат, 1956.

в §13 приводиться метод Симою (метод площадей).

2.Маковский В.А. Динамика металлургических объектов с распределёнными параметрами. – М.:металлургия,1971. –384с.

приводится метод обработки кривой разгона в случае, когда передаточная функция объекта представлена в следующем виде:

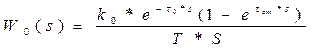τот – τ отсечки

3.Лукас В.А. Теория автоматического регулирования, учебник для ВУЗов. – М.:недра, 1990. – 416с.

приводится метод касательной, когда структура представляет собой последовательно соединённые звенья:

4.Ротач В.Я. Расчёт динамики промышленных автоматических систем регулирования. –М.: Энергия, 1973.-344с.

§11.4 приводится метод нахождения параметров структуры вида:

Рассмотрим кратко эти схемы.

В результате активного эксперимента, как в первом, так и во втором варианте получаем реакцию объекта в виде переходной характеристики. Наиболее распространены в литературе и в практике методы обработки кривой разгона объекта, как реакции линейного стационарного объекта на единичный скачок.

При обработке кривых разгона необходимо в явном виде выделить цель обработки, то есть для чего нужна получаемая при этом математическая модель каналов преобразования. В подавляющем большинстве случаев кривые разгона получают и обрабатывают для последующего выбора структуры и настройки закона регулирования.

При этом большое значение следует уделять критерию аппроксимации, то есть с какой точки зрения получаемая модель наилучшим образом аппроксимирует кривую разгона. Не все указанные выше публикации в явном виде указывают критерий аппроксимации, так, например, в книге В. А. Лукаса на странице 123после формулы (3.127) написано: “то есть наилучшей моделью динамики объекта является последовательное соединение N инерционных звеньев первого порядка с одинаковыми постоянными времени Т0 и τч (чистое запаздывание)”.

То есть совершенно не указывает с какой точки зрения такая структура модели является наилучшей. На это в явном виде обращает внимание В.Я. Ротач: ”Однако при выборе критерия приближения для определения коэффициентов этой характеристики встречаются уже ранее отмечавшиеся серьёзные трудности, в частности, с определённой осторожностью следует относиться к использованию широко распространённого метода наименьших квадратов. Обусловлено это тем, что применение такого метода позволяет получить приближения переходной характеристики в среднем на всём диапазоне её изменения, между тем, аппроксимация переходных характеристик не является самоцелью - она нужна для последующего построения системы регулирования объекта. Соответственно при использовании частотных методов синтеза о качестве получаемой аппроксимации свидетельствует не только близость самих переходных характеристик, то есть кривых разгона, сколько близость соответствующих им частотных характеристик в диапазоне частот “существенном” для разрабатываемой системы регулирования”.

Эти слова можно перефразировать следующим образом, при обработке кривых разгона следует ориентироваться не на критерии близости самих кривых разгона, а на критерии близости между АФХ- ми объекта, при чём не во всём диапазоне изменения частот, а только для третьего квадранта. Из четырёх указанных выше источников об этом говорит только В.Я. Ротач.

Таким образом, задача кривых разгона разбивается на две задачи

1. выбор структуры модели

2. оценивание параметров выбранной структуры.

В теории идентификации, как в её детерминированных, так в её и статистических размерах нет универсальных формальных методов выбора структуры моделей. Можно лишь указать некоторые инженерные приёмы, основанные на опыте и интуиции исследователей.

В рассматриваемой нами задаче чаще всего используют либо последовательное соединение инерционных звеньев с звеном запаздывания.

Например, у В.А. Лукаса:

Т0 - для всех одинаковы.

В.Я. Ротача:

В.А. Маковский предлагает:

Т – время отсечки.

τ – время запаздывания.

У Е.Г. Дудникова дифференциальное уравнение модели преобразующих каналов представлено в общем виде, как:

Исходя из инженерной практики, можно сказать, что в системах автоматического регулирования, находящихся в составе АСУТП обычно используют для моделей преобразующих каналов дифференциальные уравнения первого или второго порядка, а в системах регулирования электроприводом используют модели более высокого порядка.

Для астатических объектов, как правило, используются дифференциальные уравнения первого порядка для так называемого нейтрального объекта, когда а0=0.

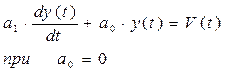Проблем особых не возникает в выборе структуры для статических и астатических объектов. Это обычно ясно из физики изучаемого объекта, а как выбрать инерционное звено первого порядка или интеграл с отсечкой здесь четких правил нет.

Если ориентироваться на приближённые инженерные методы расчета настроек регулятора, например, такие как у А.П. Копеловича, то согласно этим методикам можно ограничиться последовательным соединением инерционного звена первого порядка со звеном запаздывания. Но здесь опять же получается замкнутый кру,г исходя из системного парадокса В.Я. Ротача.

Дата добавления: 2015-07-11