Детерминированные методы идентификации.

Как детерминированные, так и статистические методы идентификации предполагают в своих постановках задачи, что эксперимент на реальном объекте уже реализован, соответствующие данные получены. Задача заключается лишь в обработке этих данных с целью построения аналитической зависимости между зафиксированными входными и выходными воздействиями или состояниями. То есть эти методы не рассматривают, за редким исключением, каким образом получены экспериментальные данные.

В детерминированном случае у функционально связана:

у=φ{v,t}

С v используется только активный эксперимент.

Условия проведения такого эксперимента следующие:

1. Объект управления должен находиться в установившемся состоянии.

2. Отсутствуют все возмущения.

3. Объект должен быть отключен от прямых и обратных регулирующих связей, то есть должен быть разомкнут.

При этих условиях в детерминированном случае классическая теория автоматического регулирования предполагает выполнение этих трёх условий, при этом входные воздействия должны быть управляемыми, то есть мы их можем изменять без каких либо ограничений, и предусматривается нанесение различных видов воздействий, в том числе и скачок.

Реакцией линейного объекта с самовыравниванием на единичный скачок является кривая разгона, которая характеризует динамику выходного воздействия объекта при единичном скачкообразном изменении входного воздействия.

Для линейных объектов, зная кривую разгона можно легко определить его реакцию на импульсное воздействие.

Для этого необходимо

1. Представить импульс как сумму двух скачков: первый из них положительный (на величину амплитуды импульса) с моментом нанесения, совпадающим с моментом начала импульса; а второй – отрицательный, величиной в две амплитуды импульса, нанесённый в момент окончания импульса.

2. Согласно принципу суперпозиции для линейных объектов реакция на импульсное воздействие также будет складываться как сумма реакций на два скачка:

3. Суммированная кривая (---) находится геометрическим сложением двух кривых.

Чисто детерминированный случай есть идеализация классической теории автоматического регулирования. В реальной ситуации при нанесении активного воздействия имеют место ошибки реализации, кроме того, при регистрации как входных, так и выходных воздействий имеют место ошибки измерения и плюс к тому эффекты влияния контролируемых и неконтролируемых возмущений.

Для таких объектов необходимо проводить многократные изменения входных воздействий с последующим их усреднением, прежде чем получить нужные экспериментальные данные.

В реальной ситуации схема (*) усложняется ещё и тем, что объект является замкнутым, то есть охвачен прямыми и обратными регулирующими связями, поэтому при снятии динамических характеристик часто используют схему активного эксперимента, изложенную в книге В.Я. Ротача “Расчет динамики промышленных автоматических систем регулирования ”. Согласно этой схеме предварительно рассмотрим свойства приведённого к выходу возмущения. При этом будем предполагать, что выходное воздействие содержит в себе как эффекты неконтролируемых возмущений, так и эффекты регулирующих воздействий. В случае если объект является, например, частью системы автоматической стабилизации, то регулирующие воздействия направлены на компенсацию эффектов возмущения. Тогда предполагается разрывать регулирующие связи, выждать некоторое время для того, чтобы свелись к нулю эффекты ранее изменяемых регулирующих воздействий и регистрировать реализацию выходных воздействий y(t) до тех пор, пока её значения находятся внутри заданного диапазона.

В соответствии с такими свойствами предлагается следующая схема получения экспериментальным путём кривой разгона:

1. Устранение всех регулирующих связей (размыкание объекта)

2. Спустя время устранения эффекта регулирующих воздействий на входе объекта наносится ступенчатое возмущение амплитудой А.

3. Регистрируются изменения регулируемой величины y(t)

4. Определяется реализация

Z1(τ)=y1(τ)-y1(0)

где у1(0) – значение выходной регулируемой величины объекта в момент нанесения скачка величиной А на входе.

5. Затем точно также после возвращения y(t) на прежний уровень наносится такое же значение пробного воздействия А и определяется значение Z2(τ)

Z2(τ)= y2(τ) - y2(0)

и так далее, реализуется n – опытов, путём длительного времени периодического размыкания и замыкания регулирующих обратных связей. В результате чего получаем ансамбль реализаций.

Полученные реализации усредняются по множеству (5)

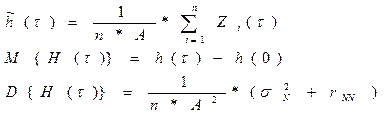Из этого выражения видно, что гладкость полученной таким путём переходной характеристики кривой разгона определяется числом n экспериментов и величиной скачка А (чем больше А и n, тем лучше).

Когда ставится эксперимент ни σN^2, ни rNNнам неизвестны, поэтому здесь можно воспользоваться оценкой дисперсии.

Допустимое отклонение ∆h(τ) или абсолютная погрешность может быть определена, как:

tT - табличное значение критерия STUDENT-а.

Зная это выражение, можно определить такое число экспериментов n, обеспечивающих допустимую ошибку ∆h(τ). И поскольку эта величина заранее неизвестна, то производятся расчеты, увеличивая n до тех пор, пока ∆h(τ) не станет допустимой. В реальной системе увеличение амплитуды пробного воздействия А ограничено диапазоном допустимых изменений y(t). Ограничено также и число разрешённых пробных воздействий.

Дата добавления: 2015-07-11