Годовое изменение параметров Земли

Прежде чем перейти к поэлементному расчету изменения параметров Земли отмечу еще раз, что в соответствии с принципом инвариантности, внешние и внутренние параметры планеты определяются ее положением на орбите. Последнее обусловливает одинаковую пропорциональную взаимосвязь внешних и внутренних свойств, что позволяет производить расчеты параметров одной системы по «комплексным» («смешанным») инвариантам. Под смешанными инвариантами понимаются уравнения, включающие как внешние параметры, например, скорость движения планеты по орбите, так и внутренние параметры, например, массу или радиус Земли. В качестве примера приведу инвариант с указанными параметрами:

М_з ∕v_з = Б, (4.11)

где: М_з – масса Земли, а v_з – ее орбитальная скорость.

Или другие инварианты:

R_n²g_n = R_nv_nз² = В, (4.12)

R_nМ_п² = Г, и т.д. (4.13)

где: R_n – орбитальный радиус в n- й день, g_n – напряжённость гравитационного поля Земли (ускорение свободного падения на поверхности планеты) в тот же день, v_nз – первая орбитальная скорость у поверхности Земли, Б, В, Г – инварианты.

В закон всемирного тяготения И. Ньютона входят m, М, R_з, G и F. В соответствии с принципом инвариантности все они должны изменяться при движении планеты вокруг светила. Диаграммы изменения скорости планеты и радиуса орбиты определены (графики 14 и 15). Теперь, опираясь на них, найдем по инвариантам (4.11)-(4.13) изменение параметров m, М, R_з, G и F. Начнем с расчета ежедневного изменения массы Земли.

Для корректного расчета изменения массы необходимо определиться с тем, на какой временной период приходится известная на сегодня величина массы равная М_з = 5,978∙10²⁷ г. Естественно предположить, что требуемую массу планета может иметь тогда, когда она находится в той области времени, в которой на графике 15 совпадают радиусы орбит, полученные по расчету инвариантов и по таблице эфемерид. И все известные параметры планеты М_з, R_з, G_з, g и т.д. следует отнести к одному из этих дней.

Вырежем фрагменты гр а фика 15 в окрестностях пересечения радиусов, полученных по таблице эфемерид – ряд 1 и по инварианту (4.4) – ряд 2, и посмотрим, на какие числа приходятся даты пересечения;

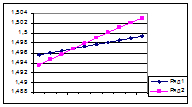На графиках 17 и 18 показаны фрагменты диаграммы годового изменения радиусов орбит исполненные по (4.3) и по таблице эфемерид. На этих фрагментах диаграммы пересекаются в двух точках: 30-го сентября 2005 г. и 6-го апреля 2006 г. Место пересечения показывает, что в эти дни расстояние

График17. График18.

от планеты до Солнца по эфемеридам лаборатории реактивного движения и по инвариантному расчету будут близки к совпадению. И, следовательно, все числовые параметры планеты для обеих диаграмм будут примерно одинаковыми. Примем массу Земли на 6 апреля равной М_з = 5,978∙10²⁷ г. и определим диаграмму её изменения за год.

Массу можно определить по нескольким инвариантам.

По изменению скорости на орбите:

М_n/v_n = const₁. (4.14)

По изменению расстояния до Солнца:

R_nM_n² = const. (4.15)

По неизменности момента количества движения µ:

R_nv_nM_n = µ = const. (4.16)

И т.д.

Результаты всех расчетов по этим инвариантам будут тождественны.

Предположим, что масса М_n рассчитывается по инварианту (4.11); тогда равенство расстояний приходится на 6 апреля 2006 г. и величина инварианта равна:

М_n/v_n = 2,0123583·10²¹ гсек/см. (4.17)

Преобразуя (4.11) относительно М_п имеем:

М_n = 2,0123583·10²¹· v_n,

и найдя, по изменению скорости движения, количественную величину массы Земли на каждый день года (приложение 2 столбец М_з), строим диаграмму изменения массы М_n (график 19).

Диаграмма М_n аналогична диаг-рамме изменения скорости движения планеты по орбите. Она свидетель-ствует о том, что масса Земли пуль-сирует с месячной и годовой частотой, изменяясь за полугодие в пределах: минимум ~ 5,893·10²⁷ г. на 24.06.2005 г., максимум 6,097110²⁷ г. на 01.01.2006 г.

График 19. Т.е. изменение величины массы наблюдается даже в первом знаке. Разница между максимумом и минимумом массы Землисоставляет ~2,049·10²⁶ г. Это почти в три раза больше принятой на сегодня массы Луны равной М_л = 7,35·10²⁵ г.

Аналогично рассчитываем изменение радиуса R_з планетыв течение года, используя различные инварианты. Например:

R_зМ_з² – const. (4.18)

Или,

R_зn v_n² – const₁, И т.д.

Для нахождения величины радиуса орбиты планеты на каждый день года используем инвариант (4.15):

R_зnМ_зn² = 2,279·10⁶⁴.

Полученные результаты занесем в приложение 2 диаграмма R_з и построим на графике 19 диаграмму R. Диаграмма R показывает, что радиус Земли уменьшается одновременно с возрастанием ее массы. Констатируем: согласно расчетам минимальный радиус R_з ≈ 6,1497 тыс. км. Земля имела 1 января 2006 г. Максимальным радиус Земли пришелся на 10 июля 2006 г. и составил R_з ≈ 6,5848 тыс. км. Амплитуда колебания радиуса ~ 435 км, Таким образом, теоретические параметры самопульсации Земли оказываются достаточно весомыми, и не могут не влиять на режим функционирования планеты и в первуюочередь погоды на ней.

Для расчета диаграммы изменения «постоянной» тяготения G_n можно также применить несколько инвариантов.

G_nv_n = const₂ (4.19)

G_n²∕R_n = const₃ = Д, И т.д. (4.20)

Для минимизации расчетов,употребим только один из них, например (4.20), причем радиусом в нем можно использовать как орбитальный радиус R_n, так и радиус Земли R_зn, естественно, что принимаются параметры по численной величине на 6 апреля 2006 г.:

G_n²∕R_зn = Д = (6,672·10^-6)²∕6,378·10⁸ = 6,97955·10^-20. (4.21)

Преобразовав (4.21) относительно G_n получаем:

G_n = √ ДR_n. (4.22)

И решив уравнение (4.22) на каждый день года, занесем полученные результаты в график 19, и получим диаграмму G изменения гравитационной «постоянной».

Таким образом, модули всех трех параметров М_n, R_зn,, и G_n оказываются синусоидально изменяемыми. Причем два из них, радиус и масса Земли изменяются в противофазе изменению гравитационной «постоянной».

Расчет силы «притяжения» можно производить по двум уравнениям:

по уравнению (а):

F_n = G_nm_nM_n/R_n² = Р_n,

и по уравнению (б):

F_n = m_ng_n.

И то, и другое уравнение предполагает «неизменность» веса тела на некоторой поверхности во времени. И в том и в другом уравнении также присутствует «неиз-менная» масса некоего пробного тела. В качестве пробного тела в данной работе используем свинцовый цилиндр весом на 6 апреля 2006 года 202,9 гр. Для получения силы притяжения F_n, например, по(б) необходимо знать изменение напряженности гравиполя График 20.планеты g_n и массы m_n на каждый день года. Напряжённость гравитационногополя (ускорение свободного падения) можно определить по инварианту:

R²g = А = 2,2014∙10²⁷ см³∕сек².

Рассчитаем изменение напряженности g и отобразим его на графике 20:

Напряженность гравитационного поля меняется за год от 9,22·10² см³⁄сек² до 10,55·10² см³⁄сек² в январе, т.е. на 1,33·10² см³⁄сек².

Осталось определиться с силой притяжения тела к Земле F и с его массой m. Силу притяжения также можно определять по нескольким инвариантам:

FR_з=Е (4.23)

F²R_з⁵= Ж и т.д.

Определимся, например, с количе- График 21. ственной величин инварианта (4.23):

FR_з²G = Е = 5,4916·10¹².

И, рассчитав параметр F_n на каждый день года, построим диаграмму графика 21. Диаграмма показывает, что вес свинцового цили-ндра изменяется с 187,33 грамма на 01.07.05 г. до 212,61 грамма на 01.01.06 г., т.е. на 25,28 гр.

Однако весы отображают величину практически на два порядка меньше. Это следствие одновременного уменьшения параметров всех тел под воздействием изменения гравиполя Земли (через массу эталонного тела).

Определим массу пробного тела исходя из параметров Земли на 6 апреля 2006 года:

m = Р⁄g = 0,20683 гр.,

и по инварианту (4.15):

v_n⁄m_n = 1,440874 = const₁,

определим количественную величину m_n на каждый день года с 01.07.05 до 01.07.06. Диаграмма графика 22 показывает, что изменение массы пробного тела за год аналогично изменению массы Земли ( график 19.) и силы при-тяжения Землей пробного тела (график 22.).Отмечу, что на графиках12-15отображены теоретические изменения параметров Земли, кото-рые при эмпирическом рассмотрении График 22. взаимодействия конкретных тел могут давать результаты, значительно отличающиеся от теоре-тических. Это обусловлено тем, что процесс измерения веса любого тела осуществляется опосредованно через некоторое промежуточное тело, илипружину,со свойствами, изменяющимися при изменении внешнего гравиполя.

4.4. Орбитальные пульсации Земли

Эту небольшую публикацию из сборника [66] с тем же названием, я привожу без изменения как при­мер орбитальной самопульсации Земли и Луны, совер­шенно не касаясь механики их движения в свете изло­женных выше электродинамических взаимодействий и с добавлением, тезисно, некоторых короткопериодических пульсаций земных сфер.

Траектории механического орбитального движения небесных тел Солнечной системы, в частности Земли и Луны, теоретически рассчитываются не по полевым уравнениям, как это делается, например, в электродина­мике, а достаточно искусственными методами возму­щающих движений. А потому правомерен вопрос: По­чему полевые методы теории гравитации практически не находят применения при расчете орбитального дви­жения планет?

Опуская рассмотрение методов возмущения как дос­таточно известных, попробую определить причины, обусловливающие отступление от полевых методов рас­чета орбит небесных тел на примере орбитального дви­жения планеты Земля.

Из классической механики известно, что планета Зем­ля движется по «инерции» на орбите в гравитационном поле Солнца со средней скоростью v_cp = 29,76 км/с, имея в перигелии скорость v_p = 30,27 км/с, а в афелии v_a = 29,27 км/с [57]. В 1995 г. по эфемеридам расстояние в перигелии от центра Солнца до Земли составляло R_p = 1,471·10¹³ см, а в афелии R_a = 1,521·10¹³ см, при среднем расстоянии R_cp = 1,49610¹³ см [108].

Воспользовавшись этими данными, определяем рас­четную напряженность гравиполя g на расстоянии, со­ответствующем этим точкам по формуле:

g_n = v_n²/R_n. (4.24)

И получаем, что в перигелии напряженность g_p = 0,62391 см/с², в афелии g_a = 0,56328 см/с², a g_cp = 0,59202 см/с².

Зная напряженность (ускорение свободного падения) гравиполя Солнца g_c = 2.738·10⁴ см/с², его радиус R_c = 6,96·10¹⁰ см и закон убывания напряженности — инва­риант (4.25):

R_с²g_c = 1,3263·10²⁶ - const, (4.25)

определяем для тех же областей пространства теорети­ческую напряженность гравитационного поля, созда­ваемую Солнцем. Она равна в перигелии g_p1 = 0,61296 см/с², в афелии g_a1 = 0,57332 см/с² и только в начале ап­реля и в октябре в моменты пересечения с расчетной, оказывается близкой к ней. Различие расчетных и теоре­тических параметров напряженности гравитационного поля уже во втором знаке (и, в частности, у Луны тоже) становится основной причиной затруднений при ис­пользовании полевых методов в расчете орбитального движения небесных тел. На диаграмме 1 графика 23 сплошной ли­нией 1отображено ежедневное расчетное изменение на­пряженности гравиполя в 1995 г., построенное по траек­тории движения Земли. Линия 2показывает реальную напряженность гравиполя на том же расстоянии от Солнца, на

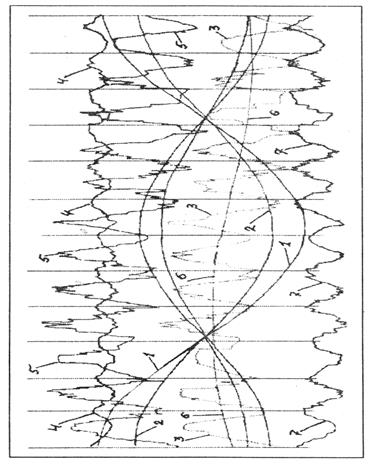
График 23

котором планета находится в соответствую­щий день. И, как явствует из диаграммы, наибольшая расчетная напряженность наблюдается в перигелии. За­тем, по мере увеличения расстояния от Солнца до Зем­ли, она, практически монотонно, убывает, сравниваясь с теоретической в начале апреля, и, продолжая убывать, достигает афелия в начале июля. В точке афелия проис­ходит перелом, и расчетная напряженность начинает возрастать, достигая средней величины в начале октября и максимума — в новом перигелии.

Фигура, образуемая этими двумя сходящимися ли­ниями, несколько напоминает полураскрытые ножницы. Угол между линиями 1 и 2 является основным препятст­вием применения полевых гравитационных уравнений. Никакого объяснения расхождению расчетной и теоре­тической напряженности мне обнаружить не удалось. И, по-видимому, современная небесная механика пренеб­регает этими ножницами, ограничиваясь при расчете траектории движения небесных тел уже упомянутым методом возмущений. К тому же классическая механика оставляет неизменными все параметры планет на про­тяжении всего их движения по орбите. А это может ока­заться одним из факторов, сдерживающих сближение теоретической и расчетной напряженностей.

Попробую, основываясь на принципах русской меха­ники, рассмотреть отдельные аспекты возможного из­менения параметров Земли при орбитальном движении.

Прежде всего, русская механика предполагает зависи­мость всех параметров движущегося тела от скорости его движения. И надо ожидать, что с возрастанием ско­рости v при движении планеты к перигелию или с ее уменьшением будет наблюдаться изменение радиуса R, гравитационной «постоянной» G, массы т, напряженно­сти гравитационного поля g и т.д. Поэтому, рассматри­вая на диаграмме 1 фактическую напряженность грави­тационного поля (линия 7) и зная, что она образуется радиусом и скоростью (4.24), необходимо определить форму связи этих внешних параметров с параметрами Земли. Например, с массой или гравитационной «посто­янной». И хотя бы предварительно определиться, будут ли они изменяться при движении планеты и каким образом.

Однако на любые изменения массы в классической механике, как уже говорилось, до сего дня наложено аб­солютное табу. Она постулируется неизменной всегда. Допускаются ее изменения только при скоростях, близ­ких к скорости света, которая, как известно, несопоставима с орбитальными скоростями, а потому при орби­тальных скоростях масса планеты меняться не может.

На изменение гравитационной «постоянной» G нало­жено табу помягче. Ее изменения допускаются. Более того, его ищут экспериментально и постоянно находят, но объяснение этому изменению в классической меха­нике еще нет.

В русской механике неизменные свойства отсутству­ют. Все свойства тел, в том числе и масса, и гравитаци­онная «постоянная» с изменением внешних условий ме­няют свою количественную величину. И потому, рассматривая медленное, почти монотонное ежедневное изменение линии 7 диаграммы 1, можно предположить, что и скорость на орбите, и расстояние от Солнца до планеты, и длина радиуса, и ее масса изменяются моно­тонно, а какая-то их совокупность остается неизменной и описывает соответствующую кривую. Задача заключа­ется в том, чтобы выделить из этой совокупности часть изменения, относящегося, например, к массе.

Классическая механика, как и русская, содержит урав-­
нение, которое включает в себя и массу т, и скорость v,
и радиус l. Это уравнение количества движения М:

M = mvl - const. (4.26)

И по законам классической механики, и по законам
русской механики (добавлю и по законам электродинамики, и квантовой механики) момент количества движе-ния, при свободном вращении или движении по орбите, всегда остается неизменным. То есть в приложении кдвижению планеты по орбите момент М по закону не может изменяться. Поскольку и в правой и в левой части
уравнения (4.26) имеются как бы неизменные величины
М и т, то его можно привести к виду:

М/т = vl - const. (4.27)

И оно будет таким при инерционном движении плане­ты по окружности, но не по эллипсу. При движении по эллипсу, как явствует из диаграммы 1 графика 23, произведение vl ≠ const, а значит и М/т ≠ const. И остается предполо­жить, что в движении по орбите меняется либо момент М, либо масса т. Поскольку момент «охраняется» зако­ном, в обеих механиках, а масса алогичным постулатом и только в одной, логично будет рассмотреть, изменяется ли масса планеты и по какому закону при ее движе­нии по орбите.

Можно, конечно, предположить, что в уравнении (4.26) меняется момент, а масса остается неизменной, или масса и момент изменяются в некоторой пропорции. Но из данных предположений следует, что изменения эти могут происходить только при некоторой форме взаимодействия движущейся планеты с окружающим пространством. Что конечно правильно и соответствует русской механике, но совершенно неприемлемо для ме­ханики классической.

В качестве точки отсчета для нахождения М было взя­то 4 апреля 1995 г., время, когда расчетная и теоретиче­ская напряженности сравниваются и, следовательно, скорость v = 2,9763·10⁶ см/с, массу т = 5,978·10²⁷ г и расстояние l = 1,4966·10¹³ см можно было принять за первичные исходные величины. В результате постоян­ная величина момента количества движения Земли по орбите оказалась равной М = 2,6628·10⁴⁷ г.см/с. (Еже­дневное расстояние до Солнца на 12 часов находим по эфемеридам [108], среднесуточную скорость определяем по [109]).

Зная величину количества движения М, преобразовы­ваем уравнение (6.19) относительно массы т:

m = M/Rv. (4.28)

Подставляя последовательно с 1 января 1995 г. в фор­мулу (4.28) ежедневную скорость и расстояние от цен­тра Солнца до центра Земли, определяем изменение ко­личественной величины массы на каждый день года и строим на графике 23 диаграмму 3. Она показывает, что масса планеты Земля, даже при относительно незначительном изменении скорости ее движения, систематически меняется в третьем-пятом знаке в пульсирующем режиме. Амплитуда колебания массы от максимума до минимума длится

около месяца, и масса изменяется от 5,972·10²⁷ г до 5,982·10²⁷ г. Изме­нение в третьем знаке происходит около раза в ме­сяц, четвертый и особенно пятый знак меняются почти ежедневно. Период одного колебания составляет около месяца и неравномерен по длительности. И в году укладывается 12 полных периодов (по результатам расчета 1994 — 1995 гг.).

Колебания переходят на следующий год таким образом, что помесячные максимумы преды­дущего года становятся минимумами последующего. Вместе с массой пропорционально пульсируют все ос­тальные параметры Земли, включая и гравитационную «постоянную» (линия 4). Именно это и фиксируется в работе [56]. Кроме того, просматривается общая для планеты волна с периодом около 12 месяцев, по-видимому, годовая (линия 6).

Пульсирующее изменение массы планеты сопровож­дается ежемесячным замедлением и ускорением ее дви­жения по орбите. И хотя относительное убывание и воз­растание скорости орбитального движения наблюдается почти на протяжении всего года, абсолютная, угловая скорость w на протяжении месяца то возрастает, то за­медляется, что и свидетельствует о пульсации планеты

Как было показано ранее, масса Земли может изме­няться только пропорционально гравитационной «по­стоянной» G по инварианту:

MG = 3,998...·10²⁰, (4.29)

где G = 6,672·10^-8 - гравитационная «постоянная».

Формула (4.29) обусловливает возможность ежеднев­ного нахождения параметра G. И по форме, и по величине гравитационная «постоянная» будет изменяться как обратное подобие изменения массы, что и наблюда­ется на диаграмме (линия 4). Следует еще раз отме­тить, что систематическое изменение G в третьем и чет­вертом знаках на протяжении полутора десятилетий фиксируется приборами [56]. Естественно, что приборы будут фиксировать не ту величину изменения гравита­ционной постоянной, которая отображена линией 4,а примерно такую, которую изображает линия 5. Аналогичным образом можно по инварианту:

M²R = 3,5736 10⁵⁶ - const₁, (4.30)

определить амплитуду колебания радиуса Земли (диаг­рамма 5). И оказывается, что месячные измене­ния радиуса достигают почти 20 км (тот же третий знак) оставаясь для нас и наших приборов почти незаметны­ми. Как тут не вспомнить А. Пуанкаре [17]: «если бы все тела Вселенной начали одновременно и в одинаковой пропорции расширяться (или, например, пульсируя, сжиматься и расширяться — А. Ч.), то у нас не было бы никаких средств заметить это, потому что все наши измерительные инструменты увеличивались бы одно­временно с самими предметами, для измерения которых они служат. После этого расширения мир продолжал бы свой ход и ничто не говорило бы нам, что произошло столь важное событие». (Курсив мой — А. Ч.)

И хотя это утверждение Пуанкаре достаточно катего­рично, в первом линейном приближении его можно счи­тать верным и подтверждаемым почти полным отсутст­вием приборной информации о пульсации Земли.

Надо отметить, что кроме двух вышеназванных пе­риодов (годового и месячного) существует хорошо из­вестный еще с древности 84,4-минутный период пуль­сации Земли — период Шулера [110], который накладывается на предыдущие и, по-видимому, имеет амплитуду колебания в пределах 1,5 км (на графике 23 он не отображен).

Можно показать, основываясь на уравнении (4.28), что и Луна в процессе своего орбитального движения от пе­ригея до перигея за полный оборот вокруг Земли совер­шает один-два цикла пульсации. Не останавливаясь на анализе представленной диа­граммы, отмечу, что полученные результаты только каче­ственно свидетельствуют о наличии пульсации у небес­ных тел — планет и их спутников. Уточненные коли­чественные величины параметров пульсации могут быть получены только тогда, когда будут сведены к одной линии гравитационные ножницы — теоретическая и расчетная напряженности гравитационных полей в об­ласти орбитального движения Земли и Луны. Их нали­чие, по-видимому, более чем на порядок искажает кар­тину пульсации Луны и в несколько меньшей степени — Земли. И именно их наличие свидетельствует о недоста­точности нашего понимания сути гравитационных взаи­модействий.

Отмечу, что орбитальную пульсацию Земли и Луны, ускорение и торможение их в процессе движения, вызы­ваемые пульсацией, можно фиксировать многими физи­ческими, астрономическими и оптическими методами, различными гироскопическими, маятниковыми и грави­тационными приборами на поверхности Земли. В част­ности, из механических приборов наиболее чувстви­тельными к самопульсации Земли являются гироскопи­ческие прецессирующие приборы типа гироскопа Фесселя.

Выявление орбитальной пульсации небесных тел по­зволяет сделать следующие предварительные выводы:

• следует ожидать, что самопульсация Земли, как и других небесных тел, вызывает попеременное, с годовым, месяч­ным периодами и периодом Шулера, замедление и уско­рение своего движения по орбите.

М = тv²/w;

• ускорение и замедление Земли на периоде в год (го­довой период пульсации) - известны, и показаны ранее;

• экспериментальное доказательство регулярного ус­корения и торможения Земли с годовым, месячным и полуторача­совым периодом при движении по орбите будет очередным доказательством отсутствия в природе движения по инерции.

Кроме орбитальной пульсации с периодом от месяца и более у Земли и ее сфер наблюдаются короткопериодические пульсации от нескольких часов до десятков ми­нут и более продолжительные, охватывающие геологи­ческие эпохи в миллионы и миллиарды лет. Изучая эти временные периоды В.А. Марков в работе [69] делает вывод о том, что «любой конечный интервал времени представляет собой циклически организованный про­цесс, складывающийся из двух зеркально отраженных в пространстве времени модельно подобных полуциклов Т₁ и Т₂ с постоянным отношением длительности T₁/T₂ = 2/3».

Этот очень важный вывод он подтверждает как при­мерами из геологической шкалы времени, так и пульсационными процессами малой временной продолжитель­ности. Пропуская рассмотрение периодов и эпох гео­логического времени, остановлюсь на короткопериодических пульсациях и в первую очередь на периоде Шулера t_i = 84,4 мин. [110]: «Применительно к t_i дели­мость в отношении 2/3 отражает пульсацию t₁' и t₁'' ос­новного тона или моды, отличающуюся от других соб­ственных колебаний наибольшей амплитудой. Ожи­даемые их значения t_i' = 0,6, или t_i' = 50,8 мин., и t_i" = 0,4 или t_i" = 33.8 мин» — пишет В. Марков [69].

Опираясь на свойства неограниченной делимости не­однородного времени, В.А. Марков построил сетку дис­кретных значений (обертонов) спектра собственных ко­лебаний Земли с рядами, как он полагает, относительной длительности 1/3, 2/3, 1/2, отличающих структуру неод­нородного времени (матрица 5)

Матрица 5

					46,22	30,80	20,54	13,68
		78,00	52,00	34,67	23,11	15,40	10,27	6,84
			26,00	17,33	11,55	7,70
43,84	29,25	19,50	13,00	8,67
21,92	14,62	9,75	6,50

В матрице за основную моду t_i' = 52 мин. приняты пе­риоды пульсации (в минутах) подтвержденные грави­метрическими [111] и сейсмическими [112] измерения­ми. Следует отметить, что по более поздним источникам [113] аналогичная мода для литосферы Земли равна 56 минутам.

Матрица, полученная В.А. Марковым исходя только из временных периодов (которую он даже не назвал матрицей), удивительна тем, что является фрагментом поперечного слоя объёмной русской матрицы. Естест­венно, что формируется она несколько иначе, чем это записано В.А. Марковым и отображает природные вре­менные обертоны. Приведу фрагмент русской матрицы 6 для короткопериодической пульсации, приняв за осно­ву моду в t_i' = 56,00 мин.

В матрице 6 основные моды короткопериодических пульсаций 84,00 мин., 56,00 мин., 37,33 мин. располага­ются по диагонали слева направо сверху вниз. (У В. Маркова основная мода расположена на горизонтали 78,00 мин., 52,00 мин., 34,67 мин.)

Матрица 6

189,0	252,0	336,0	448,0	597,3	796,4
94,50	126,0	168,0	224,0	298,2	398,2	531,0
47,25	63,00	84,00	112,0	149,3	199,1	265,5
23,62	31,50	42,00	56,00	74,67	99,55	132,7
11,81	15,75	21,00	28,00	37,33	49,78	66,37
5,906	7,875	10,50	14,00	18,67	24,89	33,18
2,953	3,937	5,250	7,000	9,333	12,44	16,59

Из матрицы 6 следует наличие еще одного полуцикла Т₃ с отношением:

Т₃/Т₁ = 1/3,

о котором есть упоминание в [69]. И полный цикл, за­вершающий процесс:

Т₂ + Т ₃ = Т₁,

есть не что иное, как элемент матричной вязи, опреде­ленный последовательностью расположения чисел на числовом поле: сумма двух последовательных верти­кальных чисел равна третьему числу, расположенному по диагонали справа налево от верхнего из них.

Можно констатировать вероятность того, что временные взаимосвязи физических параметров отображены в поперечных сло­ях русской матрицы.

4.5. Гравитационная линза Солнечной системы

Выше было показано, что расчет изменения радиуса орбиты по инварианту (4.4) выявляет иную, чем принято, величину афелия и перигелия и в результате изменения этих величин положение орбиты движения Земли относительно Солнца отличается от ныне принятого. Вот как выглядит на схеме это отличие (рис. 59.).

Таким образом, при рассмотрении таблиц эфемерид были обнаружены эмпирические явления, не описываемые классической механикой:

Рис. 59. Солнце - 1, оптическое восприятие орбиты Земли - 2, Земля в афелии и перигелии - 3, сплошная линия - истинная траектория планеты, штрихованная линия - наблюдаемая относительно неподвижных звезд траектория планеты.

• ежемесячное ускорение и замедление Земли при орбитальном движении;

• пропорциональное этому ускорению и замедлению, изменение радиусов ее орбиты;

• сдвиг траектории орбиты относительно Солнца и соответствующее сдвигу изменение эксцентриситета земной орбиты;

• практическое сохранение у сдвинутой орбиты длины большой оси эллипса.

Расчетные параметры, базирующиеся на эмпирике таблиц эфемерид, полностью меняют представление о механизмах взаимодействия тел в космическом пространстве и о самом космическом пространстве. Следует при этом еще раз отметить, что с изменением расчетных радиусов орбиты, длина линии апсид осталась практически неизменной. Однако траектория орбиты планеты оказывается сдвинутой и относительно Солнца и относительно неподвижных звезд (т.е. лучи неподвижных звезд, относительно которых определяется траектория движения Земли, достигают планету искривленными). Это очень важное обстоятельство. Оно свидетельствует о том, что существуют некоторые неизвестные пространственные обстоятельства, обусловливающие видимое (оптическое) перемещение планеты. И эти обстоятельства могут быть связаны только с вещественностью космического пространства. Поскольку только вещественное пространство (стеклянная линза, например) может искривлять солнечные лучи. Оно свидетельствует и о том, что окружающее космическое пространство представляет собой вещественное образование (ныне отвергаемый вещественный эфир) изменяемой (анизотропной) плотности.

Можно предположить, что вращающееся гравитационное поле Солнца, формирует околосолнечный вещественный эфир таким образом, что он приобретает способность преломлять (изгибать) проходящие через эфир электромагнитные и световые лучи. Т.е. придает пространству Солнечной системы свойства гравитационной линзы. Гравитационная линза, преломляя световые лучи далеких небесных тел, обусловливает возможность оптического изменения положения звезд относительно наблюдателей на Земле. В результате последние воспринимают космический мираж за истинную картину звездного неба. И наблюдатели, не замечая этого миража, получают искаженное представление о космических объектах (звездах, галактиках...), об их скорости и истинном положении в пространстве. И не замечают искажения не случайно.

Для субъекта окружающий мир как целое таков, каким он его видит (воспринимает). А космос с Земли воспринимается как невещественное пространство, как пространство изотропное. Как пустота, в которой свободно распространяются только электромагнитные поля, включая световые лучи. И данное восприятие переносится на весь космос. К тому же искусственные аппараты, как бы не взаимодействующие с внешней средой и свободно перемещающиеся в этом "пустом пространстве", подтверждают такое представление. И потому только гравитация, влияет на электромагнитные поля в пустом пространстве. Но гравитационное поле Солнечной системы, по современным представлениям, очень слабо и не может оказывать заметного влияния на электромагнитные поля.

Не придавая значения современным представлениям, допустим, что Солнечная система действительно является классической гравитационной линзой, которая преломляет проходящие через нее лучи. Т.е существует гравитационная рефракция - преломление световых лучей при прохождении ими околосолнечного эфира с изменяемой плотностью. В этом случае плоскость эклиптики разделяет линзу на симметричные половины, и планеты оказываются внутри ее на той же плоскости. И точки наиболее широкой части линзы находятся ортогонально плоскости эклиптики над и под осью вращения Солнца (рис. 60.), и свет, поступающий от звезд, только в этой точке практически не испытывает преломления. Лучи же звезд ортогональные эклиптики, падающие за пределами наиболее широкой части и, попадающие на Землю, будут отклоняться в одну сторону — к Солнцу (рис. 61.). И наблюдатели на Земле будут видеть, относительно неподвижных звезд траекторию эллипса, уменьшенного размера, но тогоже эксцентриситета.

Однако у расчетной траектории сама орбита сдвинута и относительно неподвижных звезд и относительно Солнца, да и эксцентриситет оказывается больше воспринимаемого, что необъяснимо с позиций классической механики. А это свидетельствует о недостаточной изученности и эфира, и механических, и гравитационных явлений. Известно, например,

механизме гравитации и об эфире наука до сих пор имеет достаточно скудное представление, мало чем отличающееся от представлений времен И. Ньютона.

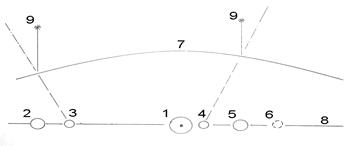
Рис. 60. Солнце - 1, Земля в афелии - 2, оптическое отображение Земли в афелии - 3, требуемое (по структуре гравитационной линзы) отображение Земли в перигелии - 4, истинное положение Земли в перигелии - 5, оптическое отображение Земли в перигелии - 6, условная поверхность гравитационной линзы - 7, плоскость эклиптики - 8, неподвижные звезды - 9.

Особенно мало известно о гравитационных полях, космических взаимодействиях, плотности космического эфирного пространства и характера движения тел в нем. Так, например, фиксируемое эфемеридами ежемесячное ускорение и замедление орбитального движения свидетельствует о том, что планета взаимодействует с пространством, в котором она движется. Однако такое взаимодействие не замечается и не описывается классической механикой. Более того, классическая механика относит орбитальное движение к инерциальному движению, к движению без взаимодействия, что противоречит наблюдаемым явлениям. К тому же в классической теории не замечается и основной вид механического движения - пульсация. И это не может не отражаться на адекватном понимании происходящих в космосе процессов и в первую очередь процессов движения и взаимодействия.

Отмечу еще раз, что в космосе наблюдаются три вида движения. Два из них перемещение и пульсация. Однако в данной работе принимается во внимание третий, симметричный способ движения - механическое и гравитационное вращение, то самое движение, которое обусловливает вращение всем телам, перемещающимся в космическом пространстве, а в микромире фиксируется как спиновое движение.

Рассмотрим ещё раз, к каким последствиям приводит механическое вращение ротора (рис. 62.). Как уже говорилось, в соответствии с классической механикой вращающийся под действием внешних сил ротор не взаимодействует с окружающим пространством (предположим, что отсутствует и воздух и тем более эфир, поскольку механика постулирует его отсутствие в природе). На ротор, как видится в этом случае, действуют только центробежные силы, которые стремятся растянуть его ортогонально оси. По мере увеличения скорости вращения происходит удлинение радиуса ротора и пропорционально ему удлинение окружности (рис.62а.). Постепенно растяжение деформирует материал ротора, деформация обусловливает появление дисбаланса и как следствие последнего - биение ротора. Материал ротора доходит до предела текучести, в нем возникают трещины, и происходит его разрушение. Этот механизм как бы подтвер-ждается многочисленными примерами аварий множества рото-ров, маховиков и других вращающихся механизмов.

Выше показан другой механизм вращения ротора, повторю его. Ротор находится не в пустом пространстве (при отсутствии воздуха), а в пространстве образованном эфиром, который проникает в него, взаимодействует с ним и "обволакивает" его в виде эфирного уплотнения ("шубы"). Когда ротор приводится во вращение, обволакивающая его плотностная эфирная шуба превращается в эфирный диск

Рис. 61. Деформация ротора по классической механике - 3а, деформация ротора по русской механике - 3б.

тороидальной формы (своего рода чечевицу летящего с большой скоростью электрона А. Лоренца), плотность и размер которого определяется как свойствами ротора, так и скоростью его вращения. Ротор же при вращении находится под сложным суммарным воздействием центробежной и центростреми-тельной сил и напряженности гравиполя Земли, которая заставляет молекулы ротора вибрировать. Особенность этих взаимодействий заключается и в том, что они имеют полевой характер и действуют на все молекулы ротора. И как бы плотен и однороден ни был ротор, эта плотность не сохраняется на уровне молекул. Поэтому при вращении по-разному изменяется частота собственного колебания молекул как относительно друг друга, так и по объему ротора. Это вызывает стремление молекул к изменению своего положения, приводит к возникновению местного дисбаланса плотности и к возникновению многочисленной локальной микровибрации.

Дополнительное воздействие оказывает на микровибрацию сжатие ротора центростремительной силой, направленной от обода к оси. Поскольку эта сила действует по сходящемуся к оси направлению, то любая ее внешняя величина стремится при схождении к бесконечности. Под действием данной силы происходит сжатие ротора (рис. 62б.) вызывающее некоторое перемещение молекул. А так как плотность и вибрации молекул по диаметру ротора неодинакова, то и сжатие их оказывается неравномерным и вызывает появление многочисленных микротрещин, а вместе с ними и возрастание частоты локальной вибрации объема ротора. Суммарное воздействие этих факторов наращивается, и если оно к тому же сопровождается возрастанием угловой скорости вращения, то рост микротрещин к ободу ускоряется. Он сопровождается усилением биения ротора, что достаточно быстро приведет к его развалу.

В этом механизме очень важна функция эфирного торроидального диска, сжимающего ротор. Он представляет собой полевое эфирное образование, обусловленное изменившимся гравитационным полем вращающегося ротора. На рис. 63. схематически показана конфигурация тороидального эфирного диска (см. выше), имеющего следующую структуру. Ротор - 1, плоскость вращения ротора и его гравиполя - 2 (или зона эклиптики для Солнечной системы и планет), зона деформированной напряженности гравиполя - 3, область наибольшей деформации - 4. Эфирный диск вращающегося ротора представляет собой зону уплотненного эфира, а, следовательно, и зону возросшей напряженности внешнего гравиполя. Этот эфирный диск обусловливает устойчивость гироскопов относительно гравитационного поля Земли. Ричард Пасечник определил эклиптику как энергетический поток неизвестного происхождения.

Именно эфирный (гравитационный) диск торроидального типа, образованный вращающимся гравиполем Солнца,

Рис. 63. Гравиротор - 1, плоскость его вращения - 2, зона деформируемой напряженности гравиполя (зона гравидиска) - 3, область наибольшей деформации - 4.

"сгоняет" планеты в плоскость эклиптики, а вращение гравиполя планет, в свою очередь "сгоняет" их спутники в плоскость планет и создает кольца вокруг них. Именно гравитационный диск создает торроидальную гравитационную линзу, обусловливающую оптическое (видимое) перемещение перигелия планеты Земля (и всех планет) к светилу (космический мираж), а афелия - от него. Границы гравитационного диска распространяются до тех зон космоса, в которых напряженность гравиполя Солнца сравнивается с напряженностью гравиполей соседних звезд, образуя нейтральную зону одинаковой напряженности.

На рис. 64., показано движение параллельных световых лучей от неподвижных звезд и их оптическое отклонение, обусловливающее наблюдаемое положение планеты относительно Солнца. Отметим, что наибольшая эфирная плотность и напряженность гравитационного поля Солнечной системы приходится на плоскость эклиптики. Это обстоятельство и обусловливает невозможность выхода планет за пределы эклиптики гравитационного торроидного диска. В отличие от математического торроида, имеющего центральное отверстие, эфирный торроидный диск "замыкается" на вращающееся небесное тело и представляет собой как бы "бублик" без дырки. Причем именно это тело, физический центр бублика, "обладает" максимальной напряженностью гравитационного поля. Гравиполе претерпевает значительные деформации при отдалении от центрального тела по оси вращения. А гравитационная линза-бублик не только искривляет проходящие через нее лучи света, но и сдвигает спектральные линии, изменяя окраску

Рис. 64. Возникновение космического миража. Солнце - 1,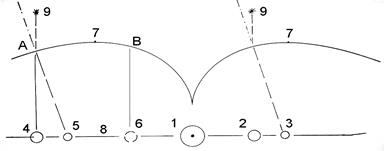

истинное положение планеты в перигелии - 2, область оптического смещения планеты в перигелии - 3, истинное положение планеты в афелии - 4, область оптического смещения планеты в афелии 5, расстояние между экстремумом афелии и перигелия - 4-6, круговая область максимальной толщины тороидальной гравитационной линзы - 7, дуга, включающая область максимальной толщины тороидального гравидиска - АВ, плоскость эклиптики - 8, неподвижные звезды - 9.

звезд и тем самым, влияя на точность определения расстояния до них. Это же явление может наблюдаться и у звезд, и у планет с космических аппаратов, движущихся к пределам Солнечной орбиты вдоль ее эклиптики, поскольку гравитационная напряженность и эфирная плотность при удалении от светила уменьшается, обусловливая фиолетовое смещение спектра испускаемых аппаратами сигналов. Именно этот фактор получил название эффекта Пионера.

К тому же у самих планет имеются свои эфирные гравитационные линзы. Эфирные гравитационные линзы планет создают местную напряженность (анизотропность) гравиполя от поверхности планет и воздействуют на распространение электромагнитных волн и световых лучей, убывая с расстоянием до нейтральной зоны равной напряженности между планетой и светилом. В результате этого воздействия происходит годовое аберрационное смещение звезд и пропорциональное ему периодическое смещение линий в спектре звезд [32].

Имеются и другие еще не наблюдаемые или наблюдаемые факторы, но не относимые к оптической линзе, которые могут подтвердить картину оптического смещения Земли гравитационной линзой. Это:

• различные изменения расстояния в системах из двух-четырех звезд при фотографировании их вдоль большой оси и ортогонально ей;

• несколько "хаотичное" распределение звезд при фотографировании их во время солнечного затмения и после него;

• гравитационная рефракция световых лучей испускаемых краем солнечного диска, уменьшающая как диаметр Солнца при полном затмении [1], так и угол изгибающих его лучей звезд;

• изменение светимости и структуры спектральных линий звезд и планет по мере перемещения наблюдателя вдоль эклиптики от светила к периферии;

• вероятно, наблюдается "приращение" годового времени относительно неподвижных звезд.

Рассмотрим один из вариантов фиксации изменения расстояния между звездами при нахождении планеты в различных областях своей траектории. Отметим, что в своем движении вокруг Солнца планета дважды за год пересекает область наибольшей толщины линзы 7 (рис. 65.), и, следовательно, световые лучи звезд, попадая в разные области линзы, по-разному искривляются в циклическом режиме. И эти искривления, попадая в приборы, во-первых, отображают фиктивное местонахождения звезды, а во-вторых, обусловливают систематическое изменение расстояния между звездами. Конечно это очень незначительные изменения, но и их достаточно для приборной фиксации. Например, следующим образом; сфотографируем в телескоп несколько звезд 4а, находящихся вдоль большой оси орбиты (рис. 65.) и вторично сфотографируем их же 5б в момент пересечения траекторией планеты области 3 максимальной толщины гравилинзы 7. Фотографии увеличим в несколько сот, а может быть тысяч раз и, наложив друг на друга, зафиксируем изменение расстояния между звёздами.

Рис. 65. Солнце - 1, Земля в перигелии - 2, Земля в области пересечения траектории орбиты с максимальной "толщиной" солнечной гравилинзы - 3. расстояние между звездами в афелии - 4а, расстояние между теми же звездами при нахождении Земли в области 3 - 5б, Земля в перигелии - 6, круговая область максимальной толщины тороидальной гравитационной линзы - 7.

Выводы:

• Ежемесячное попеременное изменение скорости движения Земли по орбите, отображаемое эфемеридами, свидетельствует о взаимодействии планеты с пространством, в котором оно перемещается.

• Пространство Солнечной системы образовано телесным эфиром, гравитационная структура которого подобна оптической линзе.

• Гравитационная линза искривляет проходящие через нее лучи света, и сдвигает спектральные линии, изменяя окраску звезд и тем самым, влияя на точность определения их истинного положения в пространстве и расстояния до них.

• Гравитационная напряженность и эфирная плотность при удалении от светила уменьшается.

Отмечу, что наличие гравитационных линз различных размеров (галактических, звездных, планетарных и т.д.) неоднократно "переворачивает" элементы звёздного неба, превращая реальную картину их расположения в некую оптическую неопределенность.

Эфирные гравитационные линзы планет создают местную напряженность (анизотропность) гравиполей от поверхности планет и воздействуют на распространение электромагнитных волн и световых лучей, убывая с расстоянием до нейтральной зоны, равной одинаковой напряженности между планетой и светилом. Они, похоже, обусловливает годовое аберрационное смещение звезд и аналогичное ему периодическое смещение линий в спектре (см. раздел 4.6) фиксируемое в настоящее время как эффект доплеровского смещения. Коротко остановлюсь на этом явлении.

4.6. Структура космологического

красного смещения

Основная информация о строении и составе космических объек­тов поступает на 3емлю с электромагнитными излучениями. Частоты получаемых излучений, приразложении их в спектр почти всегда оказываются сдвинутыми в сторону красного смещения. И чем дальше находится звездная система, тем большее красное смещение имеют ее излучения. Современной космологией предполагается, что вся величина красного смещения обусловлена доплеровским сдвигам, свидетельствующим о разбегании галактик и о расширении Все­ленной. Многочисленные попытки объяснения красного смещения другими причинами, например, гравитационным торможением или взаимо­действием фотона со своим гравитационным полем (А.Ф. Богородский), изменением гравитационной постоянной (П. Дирак и К.П. Станюкович), скорости света (В.Н. Чуриловский), изменением пространства-времени и его метрических свойств (С.Беллерт), рассеянием фотонов на фо­тонах (Г. Гофт), взаимодействие фотонов с электронами (Г. Шелтон) и другие (подробнее в обзорах [114,115]) имеют общий недостаток ­— отсутствие экспериментального доказательства своей справедли­вости.

Наибольшее распространение получила гипотеза об энергети­ческой деградации – «старении» фотона, впервые высказанная А.А. Белопольским в 1930 г. Суть ее заключается в том, что энергия свободно движущегося кванта на длительном пути движения в космическом пространст­ве, уменьшается пропорционально расстоянию от наблюдателя до объ­екта испускания. Результатом изменения энергии и является крас­ное смещение. Этой гипотезы придерживались, например, такие круп­ные физики, как Э. Шредингер и Де Бройль. Но и она не предлагает физического механизма «старения» и экспериментальной проверки процесса.

В целом гипотезы объясняющие космологическое красное сме­щение предполагают различные соотношения следующих основных факторов:

• существование пустого невещественного пространства;

• возможность изменения метрических свойств пространства-времени;

• наличие самостоятельного механизма взаимодействия для различных видов красного смещения;

• структурность фотонов;

• независимость энергетической деградации (старения) фотонов.

В течение нескольких десятилетий Х. Арп собирал эмпири­ческие факты, свидетельствующие о предполагаемом существовании красных смещений, не связанных с разбеганием галактик и воз­можном наличии не доплеровского механизма их возникновения [114,116], но прямого доказательства существования механизма им не найдено. В то же время известно, что красное космологическое смещение включает, по меньшей мере, два компонента:

• доплepoвскoe красное смещение;

• релятивистское (эйнштейновское) гpaвитационное красное смещение;

и предполагается, что физический механизм этих процессов различен.

Большие расстояния до далеких галактик и звезд, а также отсутствие представления о физических особенностях каждого из вышеназванных компонентов затрудняют разделение красных смеще­ний, а методика расчета смещений по общей теории относительности (ОТО) предсказывает полное отсутствие кpaсного смещения дляпланет и достаточно слабое для звезд и галактик, которое не меняет длины своего излучения на всем протяжения световых лучей, к тому же единственной звездой, у которой кор­ректно для изучения может быть выделено rpaвитационное красное смещение, является Солнце. Это возможно потому, что с одной стороны, расстояние до него практически не меняется, и допле­ровское смещение от собственного осевого вращёния достаточно просто учитывается, а с другой – наблюдаемое красное смещение, как предполагают, полностью объясняется в рамках ОТО, хотя по абсолютной величине красное смещение от диска Солнца почти в 3 раза меньше предсказываемой величины.

Проанализируем на графике (рис. 66.) фактическое гравитацион­ное красное смещение солнечных лучей, получен-ное в результате их спектрального разложения. Одновременно, вслед за О. Струве [31]рассмотрим объяснение гравита-ционного смещения в рамках русской механики.

Квант света на поверхности Солнца при образовании имеет длину волны λ. Покидая поверхность и устремляясь к Земле, он «теряет» свою энергию на величину GMm/R и длина его волны ста­новится равной λ₁, а энергия E:

E = hc/λ₁, и λ₁ > λ.

Разница между начальной и конечной энергией кванта рав-на:

hc/λ – hc/λ₁ = GmM/R,

где h – постоянная Планка; G – гравитационный коэффициент; m – масса кванта (фотона); M – масса Coлнцa; R – радиус Солнца.

Из уравнения Хевисайда найдем «инерциальную» массу фотона:

E = mc².

Подставляя в эту формулу начальную энергию кванта, полу­чаем:

hc/λ = mc², или m = h/λc

Рис. 66. Находим величину релятивистского красного смещения:

(λ₁ – λ)/ λλ₁ = GM/Rc² = ∆λ/λ₁. (4.31)

Формула доплеровского красного смещения имеет вид:

∆λ/λ = v/c,

и, приводя релятивистское смещение к виду доплеровского смещения убегания, получаем:

v = GM/Rc, (4.32)

где v – скорость убегания небесных тел; с – скорость света.

Формула (4.32) является основной для перевода гравитационно­го красного смещения любых небесных тел к доплеровскому виду. И она, в результате расчета, показывает незначительное красное смещение у небесных образований. Так, рассчитанное по этой формуле гравитационное красное смещение Солнца равно ~ 0,64 км/с. Фактическоеэто смещение на >80% диска Солнца (рис.66.) для большей части фотонов не превышает 0,24 км/с. И только у самого края красное смещение резко возрастает практически до пpедска­занной величины.

Факт меньшего, чем предсказывает ОТО, гравитационного красно­го смещения вызывает недоверие к себе и требует объяснения. Приведу комментарии корректности фактического крас­ного смещения Солнца астронома О. Струве [31]:

«…движения в солнечной ат­мосфере, особенно вертикальные (по-видимому, плазмы) — весьма значительны и имеют тен­денцию маскировать эйнштейнов­ское красное смещение линией поглощения. Но на лимбе Солнцадоплеровские смещения, обусловленные компонентами движения по лучу зрения, малы. Поэтому ис­тинное эйнштейновское красное смещение проявляется наиболее отчетливо при измерениях длин волн на самом краю солнечного диска».

Фактическое красное смещение солнечных лучей не устраи­вает и П.Н. Кропоткина, который со ссылкой на Д. Крауфорда пока­зывает, что краевой эффект красного смещения обусловлен тем, что световые лучи, идущие «… от края диска, проходят в поле относительно высокого гравитационного потенциала более значи­тельный путь, чем лучи от центра диска» …и именно они со­ответствуют формуле А. Эйнштейна [115].

Если же довериться эмпирическому факту и допустить, что горизонтальная прямая АВ (рис. 66.) красного смещения диска электромагнитного излучения Солнца является действительным фак­том, то возникает вопрос, а что же выражает пик краевого красного смещения?

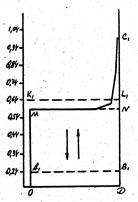Я полагаю, что на графике (рис. 66.) мы имеем дело не с од­ним гравитационным красным смещением, а с двумя различными смещениями. Одно на уровне 0,24 км/с – истинно гравитационное смещение, вызванное воздействием напряженности гравитационного поля Солнца на испускаемые фотоны. А другое, от 0,24 до 0,64 км/с, — не гравитационное краевое смещение, гипотеза о природе которого будет рассмотрена ниже. Отмечу, что эффект краевого красного смещения можно наблюдать не только в Солнеч­ных лучах. Покраснение лучей восходящего и заходящего Солнца, наблюдаемое с Земли, имеет ту же физическую природу. И хотя часть этих лучей в момент восхода и захода рассеивается и поглощается воздухом (рассеивание Рэлея) и находящимися в нем микропылинками, вызывая эффект некоторого покраснения диска, значительная часть покраснения, по-видимому, обусловлена кpaeвым крас-ным смещением у поверхности 3емли.

Рис. 67.Это предположение можно проверить, зафиксировав гамму лучей восходящего или заходящего Солнца с поверхности 3емли. На графике (рис.67.) показано качественно то красное сме­щение, которое следует ожидать на такой спектрограмме. На этом графике прямая A₁В₁ по высоте A₁0 имеет ту же величину, что и АВ на графике (рис. 66.) и полностью относится к гравитационному красномусмещению. Прямая MN является суммой гpавита­ционного красного смещения све­тового луча A₁О, обусловленного гравиполем Солнца и краевого смещения Земли A₁N.

И, наконец, C₁N (рис. 67.) есть краевое смещение, полученное при прохождении лучей вблизи Солнца почти по касательной к ее поверхности, и имеет ту же форму и размеры, что и СВ на графике (рис. 66.).

Из сравнения графиков можно констатировать,что на протяжении светового дня красное суммарное смещение с максимальной величиной МN при восходе Солнца к середине дняуменьшается до минимального уровня A₁B₁ и снова возрастает до MN на закате (показанострелками на рис. 67.), Т.е. является переменным пapаметром. Особенно четко и без атмосферных помех это возвратно-поступательное движение красного смещения по шкале спектра можно наблюдать с орбитальных станций, только абсолютная величина ОМ (рис. 67.)в этом случае будет зависеть от ориентации плоскости орбиты относительно Солнца, от радиуса орбиты и от местона-

хождения станции на орбите.

Рассмотрим поведение краевого красного смещения в зависимости от поверхности испускания и приема на околоземной орбите и на Земле. Так, если световой луч, идущий от центра диска О Солнца к лаборатории А на поверхности Земли (рис. 68.), практически не имеет краевого смещении (везде фиксация лyчa производится разложением в спектр и гравитационное смещение не рас­сматривается), то луч из точки Д на краю к А принесет такое покраснение(СВ на рис. 66.). Свет от О к В также будет иметь краевое красное смещение, но это смещение вызвано Землёй (образует горизонтальную прямую MN и по абсолютной величине равно NB₁ (рис. 67). Луч, исходящий из С и фиксируемый в пункте В, принесет суммарное краевое покраснение от Солнца и от Земли С₁В₁ (рис. 67.).

Изучение структуры и параметров краевого смещения наиболее удобно проводить с борта орбитальных космических станций. Изменение положения станции на орбите позволяет исследо­вать как краевое смещение от 3емли (OEF рис. 18.), так и суммар­ное смещение от Земли и Солнца СFM (рис. 18.). При этом изменения от ЕF до Е₁F₁; (рис. 18.) и более покажет изменение краевого сме­щения по радиусу. Отмечу, что станции, находящиеся на орбитах, перпендикулярных солнечным лучам, не будут фиксировать возврат­но-постyпа-тельного движения краевого смещения Земли.

Рассмотрим физические основы всех составляющих космологи­ческого красного смещения. В работе [59] и выше показано, что тела и, в частности, электромагнитные волны, движущиеся в гравитацион­ном поле, меняют свои параметры по линейной закономерности про­порционально изменению напряженности g гравитационного поля, а последнее образует вокруг любых тел нейтральную зону равной напряженности гравиполей взаимодействующих тел.

Рис. 68.

Линейная зависимость гравитационного красного смещения не коррелирует со смещением, получаемым по (4.32). Taк, теоретически световой поток, движущийся вертикально с поверхности Земли, не должен иметь гравитационного смещения и поэтому его нельзя за­фиксировать с помощью спектрометра.

Надо отметить, что справедливость формулы (4.32) для светового луча, идущего вертикально от поверхности Земли на пути 20 м, проверялась с помощью эффекта Мессбауэра [118]. Наличие очень слабого гравитационного смещения, с точностью до 1% подтверждающего теоретические расчеты, было доказано. Но нельзя исключить совпадение на каком-то отрезке пути расчетных результатов с экспериментальными, обусловлены линейным расширением длины волны [59]. Для проверки можно предложить другую постановку эксперимента. Достаточно направить из пункта G (рис. 68.) поверхности Земли световой луч в точку М, например, на орбитальную станцию, и рассмотреть спектр полученного излучения. Если расстояние до станции равно 1,3·10⁷ см, а длина волны λ = 4·10^{-5 см, то на станции зафиксируют длину волны λ} ₁ = 4,082·10^{-5 см, а это равнозначно убеганию Земли от станции с достаточно скромной скоростью – 600 км/сек. (Без учета гравитационных изменений параметров станции).}

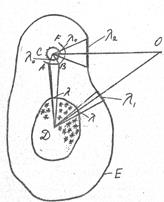Изменение гравитационного смещения будет особенно заметно при наблюдении его у физически взаимосвязанных систем, напри­мер, галактики и ее спутника (рис. 69). Поскольку галактика Д и ее спутник С имеют единую нейтральную зону Е с окружающими галактиками но совсем другую зону равной гравитационной напряженности. АBF между собой, то это обусловливает испускаемому ими излучению различное грави­тационное смещение для галактикии ее спутника, и следовательно, создает впечатление о том, что наблюдаются различные физические системы.

Рис. 69. Положение нейтральной зоны АВ между галактикой и ее спутником полностью опpeделяетсясоотно­шением линейных параметров фигуры ABCD (рис. 69.) аналогично фи­гуре АOBD (рис. 4.). Предположим, что с плотной стороны галактики испускается световой луч в сто­рону спутника с длиной волны λ и принимает плотной части спутника λ, причем λ = λ

Дата добавления: 2015-07-12