Третье началоКТД известно как теорема Нернста [121,122], следствием которой является так называемый принцип недостижимости нуля абсолютной темпе­ратуры. 7 страница

Не обсуждая подробности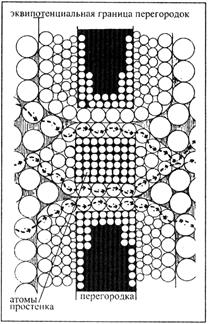

самого эксперимента с движением электронов че-рез отверстия перегородки, покажу, что представляет собой пространство в окрест­ностях перегородки с двумя открытыми щелями (рис. 79.), а также с одной закрытой щелью (рис. 80.). И станет понятно, как будет двигаться электрон при двух открытых щелях, попадая даже в сере-дину простенка.

На рис. 79. с левой сторо-ны молекулы эфира, через ко­торые пролетает электрон на пути к перегородке, справа ¾ молекулы перегородки, а за Рис. 79. ней снова до экрана про­странство эфира. Его траектория определяется той скоростью, которая была придана ему импульсом от­рыва (разгоном) от излучателя. Скорость отрыва обу­словливает электрону движение в атомах и молекулах строго по определенной траектории и вход в эквипо­тенциальную поверхность молекул перегородки под со­ответствующим углом (рис. 79.). Движение в эквипо­тенциальной зоне молекул пульсирующей перегородки будет проходить в промежутках между пучностями, что и обеспечивает электрону возможность выхода из зоны действия этих молекул на некотором как бы квантованном пучностями расстоянии от электронов, имеющих даже незначительное отличие от него в скорости. Эти незначи­тельные отличия приводят к тому, что электроны «входят» в эквипотенциальное про­странство молекулы под раз­личными углами, двигаются в этом пространстве по различ­ным узлам и выходят за пере­городкой из различных точек ее эквипотенциального про­странства. Вот тот процесс, который и вызывает появле­ние интерференции на экране.

Наличие двух щелей в перегородке качественно меня­ет картину движения электрона. Надо помнить, что расстояние между щелями по порядку величины не может быть больше длины волны электрона, а это значит, что эквипотенциальные поверхности щелей и простенка перекрываются, а собственная пульсация простенка усиливает стоячие волны в обеих щелях, что приводит к более четкому разделению электронов в пространстве щелей и в их движении к экрану. К тому же перегородка образует в направлении излучателя не­которую выпуклость (рис. 79.), оканчивающуюся «сред­ним» атомом, как раз имеющим радиус примерно рав­ный половине волны электрона. Электроны, «налетающие» на этот атом ниже или выше его ядра (по рис. 79.), будут «направляться» (модулироваться) эквипотенциальным полем атома либо в одну, либо в дру­гую щель. На выходе из щели он отрывается от послед­него атома перегородки под несколько большем углом, чем тот, под которым входил в пространство первого атома. Вот те обстоятельства, которые обусловливают появление на экране интерференционной картины.

При одной открытой щели модулятор отключается «заслонкой» (рис. 80.), и эквипотенциальная поверх­ность от стенок щели к ее центру изменяется примерно одинаково (т.е. структура пространства вокруг щели изменяется, становясь такой же, как и при одной щели), электроны, попадая в одинаковые условия перед ще­лью, распределяются за перегородкой тоже примерно одинаково, большая часть из них сосредотачивается на­против центра щели, так как напряженность поля там наименьшая.

Поскольку при закрытии одной щели «выпуклость» модулятора перед пе­регородкой и за ней исчезает («погашают­ся» плотностью за­слонки), то исчезают и условия, обеспечи­вающие модулирова­ние электронов по эк­рану, а вместе с ними прекращается процесс интерференции. Несколько слов о мысленном«пулемете» Р. Фейнмана.

Именно модель «пулемета» как прообраза, сопос­тавляемого с квантовой моделью, наглядно показывает те нюансы, которые были упущены при выдвижении квантовой гипотезы. Чтобы мо-дель «пулемета» кор­ректно соот-ветствовала квантовой модели с щелью или двумя щелями, пере- Рис. 80 городка с отверстиями для пролета пуль должна быть сделана по толщине из десятков тел радиусом, равным радиусу Земли. Тела эти должны на­ходиться друг от друга на расстоянии, не меньшем ее диаметра, ширина щелей ¾ близка расстоянию от Земли до Луны. «Пулемет» должен находиться на расстоянии сопоставимом с расстояния до Солнца, и стрелять «пу­лями», имеющими скорость полета намного больше второй космической скорости (>>11,5 км/с). Вот такая конструкция макромодели «пулемета» будет до некото­рой степени соответствовать структуре модели с двумя щелями для пролета электронов. Естественно, что вы­воды из стрельбы такого «пулемета» в перегородку с двумя отверстиями будут несколько отличаться от тех, к которым подводит студентов знаменитый курс лекций.

Поскольку, как совершенно правильно констатирует Р. Фейнман, нам еще не дано наблюдать за электроном, не нарушая траектории его движения, мы не сможем проследить его путь и, следовательно, точку, куда по­падет конкретный электрон. Но из этого вовсе не следу­ет, что траектория движения у него полностью отсутст­вует, и мы не можем, задаваясь исходными параметрами электрона и зная количественные характеристики про­странств и отверстий, через которые он проходит, точно рассчитать его путь. Для теории в этом запретов нет. Есть технические ограничения для эмпирического под­тверждения теории и связано оно с недостижимостью необходимой точности в экспериментах. Эксперимента­тор не имеет (на сегодня) приборных возможностей оп­ределить, из какой щели вылетел электрон или в какую он влетел уже потому, что для этого необходимо найти точку вхождения последнего в пространство атома с точностью на порядок меньше длины волны электрона.

И, похоже, можно предложить эксперимент, позволяющий направлять полет электрона к строго определенной
щели и не влияющий на его движение по выходу из нее.
Это можно сделать следующим образом: Установить
электронную пушку 1внутри направляющего канала 2,
ведущего к двум щелям, и на некотором расстоянии от
нее по направлению к щелям разделить канал перего­родкой 3на два канала, один из которых подходит к щели 4, а другой к щели 5 (рис. 81). В каждом из кана­лов может быть установлен либо световой, либо электромагнитный индикатор 6, который и зафиксирует прохождение электрона по каналу до того, как он дос­тигнет щели. И возмущение, полученное электроном при фиксации, не будет отражаться на его поведении после прохождения через щель. Т.е. будет отсутствовать искажение интерференционной картины.

Появ­ление же интерфере-нции обусловлено наличи-ем модулято­ра перед щеля-ми (перегородка в канале) и за щелью (утолщение в простенке)

Рис. 81. Таким образом, мож­но представить реаль­ный механизм «для оп­ределения того, через какое отверстие прохо­дит электрон» и тем самым еще раз поста­вить под сомнение принцип неопределен­ности. Другое дело, что выполнить перегородку для прибора толщиной в пол-атома современная промыш­ленность не в состоянии. Но это технические трудно­сти, а не физические. И хотя еще нет физических спо­собов проследить, не влияя на электрон, по какой же траектории проходит его полет, можно однозначно утверждать, что электрон летит по траектории, определяемой электромагнитной напряженностью поля атома. Данное обстоятельство, по-видимому, будет до­казано только тогда, когда экспериментаторы нау­чатся работать с эфиром и его образованиями. Это время еще наступит.

6.5. Нецелочисленные радиусы орбит в атоме

Ранее было показано, что вурфные отношения золо­тых пропорций описывают взаимосвязи различных па­раметров одной системы и характер их зависимостей. Это свойство вурфных отношений может быть исполь­зовано для определения полноты различных числовых рядов. Рассмотрим, используя вурфы, например, полноту и целочисленность электронных орбит в атомах.

Как уже говорилось, одно из главных предположений Бора, обосновывающих структуру теории строения ато­ма, сформулировано следующим образом [139]:

«Основное» состояние любой системы, т.е. состояние, при котором излученная энергия максимальна, опреде­ляется из условия, что момент импульса каждого элек­трона относительно центра его орбиты был бы целым, кратным h/2p». (То есть целочисленным. - А. Ч.)

Согласно, этому предположению (постулату), внутри атома из бес­численного множества возможных орбит электрона реа­лизуются стационарные, орбитальный момент которых равен целому числу n, кратному h. Стационарные орби­ты (по Бору, ¾ единственно допустимые в атоме - А. Ч.) нумеруются целыми числами от 1 до бесконечности [144]: n = 1,2, 3,... ¥ (если это так, то какой же диаметр име­ет атом с галактику? Или больше? - А.Ч.), и постулируется, что данный ряд значений орбит полон, и существование других, промежуточных орбит с «нецелочислен-ными» номерами, невозможно. И потому n стало главным квантовым числом, открывшим систему квантования электронных орбит, а вместе с ними и квантовую меха­нику. Одновременно неявно постулировалась заданность и жесткость образующейся системы:

• все структурные взаимосвязи электронов однознач­но привязывались к п;

• постулировалась незаполненность пространства между ядром и боровской орбитой;

• боровский радиус практически становился и внеш­ней границей атома, и началом электронных орбит, создавая тем самым неопределенность статуса возни­кающей структуры, поскольку за границей атома начи­наются пространства других атомов.

Нарушение целочисленности орбитального момента, (существование между целочисленными промежуточных орбит), выявленное при совместном решение уравнений Бора (6.7) и Де Бройля (6.6) ставит под сомнение существование не только целочисленных орбит, а вместе с ними и корректность и полноту всей квантовой механики. (Как следует из таблицы 22, промежутки между целочисленными орбитами заполнены еще неизвестными нецелочисленными орбитами электронов, они то и «образуют» промежуточные орбиты).

Для исследования полноты и целочисленности пара­метров электронных орбит а, v, Е, при n = 1,2, 3,..., 10, выпишем их количественную величину на первой боровской орбите из [30]:

а = 0,5292·10^-8 см - радиус боровской орбиты элек­трона, v = 2,188·10⁸см/сек.- его скорость на этой орбите, Е = 2,181·10^-22 - энергия электрона на 1 -й боровской орбите.По известным уравнениям кван­товой механики, найдем количественную величину указанных параметров на n -х орбитах:

а_n = n²h²/me²; v_n = е²/nh; Е_n = me⁴/ 2 n²h². (6.12)

И занесем в табл. 23 по нисхо­дящей величине степени столбца п (нулевая строка таблицы). Добавляем в первую строку табл. 23пара­метры массы электрона т = 9,110·10^-28 гр., заряда е = 4,803·10^-10, удельного заряда f = 5.273·10¹⁷, атомной гравитационной «постоянной» G = f² = 2,780·10³⁵, скоро­сти света с = 2,998·10¹⁰, и «постоянной» Ридберга R_¥ = l,097·10⁵ для бесконечной массы. Вносим в первую строку параметры частоты w и приведенной частоты u, рассчитав величины их столбцов пo уравнениям:

w_n = v/а_n; w_n = 2 pu_n

Таблица 23 заполнена. Даже по внешнему виду она достаточно непривлекательна и вызывает сомнение в своей истинности уже потому, что объединяет как бы в одну систему взаимосвязи, не подобные по своим свой­ствам, а потому и не связуемые качественно параметры: часть столбцов 3, 10-13, заполнена переменными вели­чинами, а столбцы 4-9 заполнены только в боровской строке так называемыми «фундаментальными постоянными». Каков механизм связи постоянных величин с пе­ременными, в квантовой механике не объясняется, а просто в неявной форме постулируется существование такого механизма.

Основная зависимость между переменными параметрами в табл. 23 образуется постулируемой целочисленностью орбит. Именно степень номера орбиты становится тем коэффициентом, который и обусловливает как взаимосвязь между «постоянными» и переменными параметрами, так и коэф-фициентную структуру изменения переменных параметров. Степенная величина коэффициента, образуемая номером орбиты для каждого параметра, вынесена в нулевую строку табл. 23 под индексами параметров.

Применив найденные в работе [15] инварианты:

ħ=а_nv_nm=е_n²/v_n=f_nе_nm_n/v_n=m_n²G_n/v_n=Е_n/w_n=Е_n/ 4 pс_nR_¥n. (6.13)

Убедимся, что соответствующая им постоянная Планка (ħ) может быть получена, как показано ранее, несколькими способами только с использованием величин параметров боровской строки табл. 23. По величинам параметров других строк (орбит) получение ħ без дополнительных постулатов не представляется возможным.

Фактически это означает, как уже отмечалось, что электрон, находящийся на первой орбите, движется и взаимодействует с ядром по одним законам, а с переходом на другую орбиту меняет систему взаимодействия и движется на них по другим законам, причем на каждой орбите по иному закону. В теории атома постулированием целочисленности орбит подбираются такие зависимости, которые обеспечивают «сшивание» переменных и «постоянных» величин только ограниченного количества параметров и, следовательно, уравнений. И только такие уравнения находят применение в современной квантовой механике. Совершенно корректный комплекс уравнений (6.13) не применим в ней уже потому, что никакими целочисленными величинами ¾ коэффициентами невозможно обеспечить в нем взаимосвязь «постоянных» и переменных параметров, поскольку в нем возможно использование только величин взаимосвязанных переменных параметров.

Таблица 23

		а	G	f	е	m	с	R	v	Е	w	u
	0	n^2	n^1	n^1	n^1	n^1	n^1	n^1	n-^1	n^-2	n^-3	n^-3
	1.	0.529	2,780	5,273	4,803	9.110	2,998	1,097	2,188	2,181	4,134	6,581
…	…	… …	…	…	…	…	…	…	…	…	…	…
	2.	2,117							1,094	0,545	0,515	0,822
…	…	… …	…	…	…	…	…	…	…	…	…	…
	3.	4,763							0,729	0,242	0,153	0,244
	4.	8,462							0,547	0,136	0,065	0,103
	5.	13,29							0,438	0,087	0,033	0,053
	6.	19,05							0,365	0,061	0,019	0,030
	7.	25,93							0,313	0,044	0,012	0,019
	8.	33,87							0,273	0,034	0,008	0,013
	9.	42,87							0,243	0,27	0,006	0,009
	10.	52,92							0,219	0.022	0,004	0.007

Имеются такие невостребованные уравнения и в клас­сической механике. Выпишем некоторые из них [62]:

m_nG_n = W_nG_n / v_n² = т_пv_n⁴R_n/W_n = v_n⁴R_n²/m_nG_n =

W_nR_n²v_n²/m_n²G_n =…= const, (6.14)

и отметим, что эти уравнения, как и постоянная Планка ħ, являются инвариантами и не находят применения в классической механике только потому, что масса тела т постулируется неизменной как во взаимодействиях, так и при изменении телом положения в гравитационном поле. А гравитационная «постоянная» G остается одной из «фундаментальных постоянных» классической механи­ки.

Таблица23, за исключением «фундаментальных по­стоянных», представляет собой матрицу размерностных па­раметров, связанных степенной зависимостью по стро­кам и столбцам. И еще не найден математический аппарат, позволяющий определять полноту и совмести­мость образованного матрицей квантованного числового поля, а, следовательно, и корректность орбитальных за­висимостей боровской модели атома. Аппарат, приме­няемый в квантовой механике, такую задачу решить не в состоянии, поскольку в определении полноты и совмес­тимости элементов квантовой механики опора на внут­ренние структуры теории не дает определенного ответа. Требуется внешний, относительно теории кван­товой механики, математический аппарат, например, уже упомянутая система вурфных отношений [37]. Она обладает следующими достоинствами:

• базируется на степенных взаимосвязях русской матрицы;

• не является составной частью ни одной теоретиче­ской или математической системы, а потому ¾ внеш­няя для аппарата квантовой механики;

• охватывает матричную структуру, как по строкам так и по столбцам;

• позволяет определять взаимосвязи многих параметров;

• проста и эффективна в расчетах.

Вурфные отношения ¾ абстракции и образуются либо взаимосвязанной системой коэффициентов, либо без­размерными модулями степенных параметров. Они от­ражают не количественные взаимосвязи между пара­метрами, а качественные отношения значимостей в матрицах, составленных из численных величин параметров. То есть с их помощью можно определить, обладает ли числовое поле рассматриваемой матрицы качествами природной системы.

Для проверки полноты параметров табл. 23 берутся, как уже говорилось, три последовательных значения па­раметры ¾ a, b, c и подставляются в вурфное отношение [37]:

W (а,b,с)= [(а + b)(b + с)] /b (а + b + с). (6.15)

Если все получаемые коэффициенты имеют одинако­вую величину или монотонно изменяются, ряд парамет­ров полон и не противоречив. Если же такая зависи­мость отсутствует, данный ряд либо не полон, либо не совместим.

Используя уравнение (6.15), проведем проверку пара­метров a, v, E табл. 23 на полноту и совместимость с вурфными уравнениями по всем строкам. Для а и v име­ем;

W_1а (0,5292;2,117;4,763) = 1,1607; W_lv (2,188;l,094;0,7293) = 1,3636, W_2а (2,117;4,763;8,462) = 1,2451; W_2v (1,094;0,729;0,5470) = 1,1143, W_3a (4,763;8,462; 14,28) = 1,2821; W_3v (0,729;0,547;0,4376) = 1,3404, W_4а (8,462;14,28;19,05) = 1,2973; W_4v (0,547;0,438;0,3647) = 1,3379, W_5a (14,28;19,05;25,93) = 1,3104; W_5v (0,438;0,365;0,3126) = 1,3359, W_6а (19,05;25,93;33,87) = 1,3155; W_6v (0,365;0,313;0,2735) = 1,3356,

W_7а (25, 93;33,8742,87 ) = 1,3204; W_7v (0,313;0,273;0,2431) = 1,3351,

W_8а (33,87;42,87;52,92) = 1,3224; W_8v (0,273;0,243;0,2188) = 1,3347.

Для Е аналогично получаем следующую величину ко­эффициентов:

W_1e = 1,3265; W_2Е = 1,3320; W_3E = 1,3328; W_4E = 1,3334;

W_5E = 1,3330; W_6E = 1,3334; W_7e = 1,3333; W_8E = 1,3333.

Вурфные отношения свидетельствуют о том, что коэффици­енты параметров столбцов радиусов орбит а содержат скачок, и, следовательно, вурфный критерий по столбцам не выдерживается. Еще больший скачок отмечается между первым и третьим вурфным коэффициентом ско­рости v. Поэтому можно сделать следующие выводы:

Первое. Значительный скачок вурфных коэффициен­тов радиусов и скорости по второй строке свидетельствуёт о том, что между орбитами 1-7 имеются «прогалы», места возможных промежуточных орбит. Эта же карти­на, хотя и не такая резкая, наблюдается и по остальным параметрам (например, по Е). Их более плавное изменениe объясняется, вероятно, тем, что они «привязаны» к номеру радиуса и «повторяют» его поведение с иной степенной последовательностью. Изменение знаменате­ля последовательности сглаживает возрастание вурфов.

Второе. Вурфы первых трех параметров представлены коэффициентами различной количественной величины, а это свидетельствует, по-видимому, о рассогласованно­сти параметров величин данных столбцов с системой, которую они образуют.

Третье. О внутренней противоречивости свидетельст­вует и невозможность использования в вурфных отно­шениях «фундаментальных постоянных», входящих в таблицу 23. Именно наличие постоянных и переменных величин образует неполноту и несовместность орби­тальных параметров по столбцам.

Прежде чем рассматривать совместимость перемен­ных параметров табл. 23 по строкам, обратим внимание на то, что часть столбцов является восходящими от бо­ровских величин, а часть нисходящими. В табл. 23 вос­ходящим (возрастающим) является только радиус а, ос­тальные ¾ нисходящие (уменьшающиеся). Вурфный анализ по строкам возможен либо по восходящим, либо по нисходящим параметрам. Проведем его, например, для параметров скорости v, частоты u, и энергии Е по строкам 1 - 8....

Выпишем величины v, u, E из соответствующих строк:

W₁ (2,188;2,181;6,580) = 1,603,

W₂ (1,094;0,5452;0,8225) = 1,670,

W₃(0,7293;0,2423;0,2437) = 1,604,

W₄(0,5470;0,1363;0,1028) = 1,525,

W₅(0,4376;0,0872;0,0526) = 1,457,

W₆(0,3646;0,0606;0,0305) = 1,402,

W₇(0,3125;0,0445;0,0192) = 1,358,

W(0,2735;0,0341;0,0128)= 1,322.

О вурфной совместимости рассматриваемых парамет­ров может свидетельствовать более или менее посте­пенное, стремящееся к монотонности изменение резуль­тирующего коэффициента по строкам. Чем строже монотонность, тем больше совместимость параметров. Резкий скачок коэффициента W = 1,670 свидетельствует о том, что входящая в него первая тройка величин пара­метров не соответствует критерию совместимости.

Таким образом, вурфный критерий на совместимость величин параметров табл. 23 не выдерживается и по строкам, а это ставит под сомнение внутреннюю непро­тиворечивость постулируемых целочисленно кванто­ванных орбитальных моментов.

То, что количественные величины столбцов числового ряда a, v, u, Е, обусловленные целочисленными номе­рами орбит, не образуют единого по столбцам вурфного коэффициента полноты, свидетельствует об искусствен­ности принятой системы орбитального квантования. Об этом же свидетельствует отсутствие взаимной со­вместимости коэффициентов величин параметров в строках табл. 23.

Искусственность целочисленного квантования под­тверждается и комплексом уравнений (6.13), заполнение которого параметрами строк (кроме первой) табл. 23 не обеспечивает получение постоянной Планка.

И можно полагать, эта искусственность квантования обусловлена неосознанным стремлением разработчиков квантовой системы оставить, посредством постулиро­ вания, неизменными сложившиеся представления о «фундаментальных постоянных». Целочисленные орби­тальный момент, построенный на «фундаментальных постоянных», т_е, е, с, R_¥ резко ограничивает использо­вание всей палитры природных параметров в квантовой механике, отсеивая все из них, несовместимые с целочйсленностью, создавая мощнейшее «прокрустово ло­же» квантования и обеспечивая фиктивную базу для формирования законов движения в микромире, отличных от законов классической механики. А потому поня­тийный аппарат квантовой механики, базирующийся на главном орбитальном квантовом числе и неизменных «фундаментальных постоянных», не может считать­ся корректным.

Имея представление об искусственном возникновении целочисленности орбитального квантования и об отсут­ствии в природе «фундаментальных постоянных», по­пробую предложить иную систему функционирования электронных орбит в атомах.

Отмечу, что самым важным результатом использова­ния целочисленного квантования становится, по-види­мому, представление о том, что орбитальные парамет­ры движения электрона в атоме изменяются в соответствии с определенными, надо полагать, естественными коэффициентами; функции которых и под­менялись степенями целочисленных номеров орбит.

В главе 2 и в работе [62] показано, что все параметры любой физической системы связаны между собой есте­ственными качественными коэффициентами значимостей золотого множества. Эти коэффициенты входят ба­зисным столбцом в гармоничную русскую матрицу. Основу их составляет малая секунда темперированного музыкального ряда, иррациональное число ¾ 1,059463...... И каждое физическое свойство как бы содержит в себе степень данного числа как элемент качественной связи с другими свойствами. Именно качественные связи ме­жду свойствами и обусловливают существование ме­тода размеренности в физике. Поэтому, основываясь на естественных связях качественных значимостей, пред­лагается построить систему взаимозависимостей пара­метров орбит в атоме.

Отмечу также, что в природе, на всех уровнях, отсут­ствуют неизменные, самотождественные тела и свойст­ва, а потому качественные значимости придают всем количественным величинам элементарных параметров макро- и микромира статус взаимосвязанных перемен­ных величин.

Руководствуясь этими соображениями, составим табл. 24 изменения параметров орбит электронов в ато­ме. Столбцы ее открываются индексами тех же парамет­ров, которые наличествуют в табл. 23, а их количествен­ные величины в первой строке в точности (кроме Е) соответствуют первой строке табл. 23.

Под индексами параметров электронных орбит в ну­левую строку табл. 24 заносим их качественные значи­мости из главы 2. Эти значимости выполняют по столб­цам табл. 24 функции степенных коэффициентов, обеспечивающих изменение величины соответствующе­го параметра электрона при переходе его с одной орби­ты на другую. А потому показатель степени у значимостей одной строки таблицы оказывается одинаковым.

Данная методология до некоторой степени повторяет методологию Бора, но исключает стационарные орби­ты, а вместе с ними и определяющую роль целочислен­ной нумерации, которую заменяют качественные значи­мости ¾ коэффициенты системной взаимосвязи веще­ственных параметров.

Дата добавления: 2015-07-12