Домашней контрольной работы № 2

Пример решения типового варианта

1 Вычислить определенные интегралы:

а) б) в)

Решение

а)

б) Воспользуемся методом интегрирования по частям. Положим откуда Тогда:

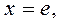в) Положим ;тогда ;если то ; если то

Следовательно,

2 Найти радиус и область сходимости степенного ряда:

a) б) .

Решение

а) Радиус сходимости данного ряда вычисляется по формуле

.

Здесь .

Тогда

В данном примере 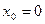, поэтому интервалом сходимости ряда будет (-1,1).

Исследуем поведение ряда на концах интервала сходимости.

Подставим в ряд сначала , а затем . При имеем . Этот ряд знакочередующийся, он сходится по признаку Лейбница. В самом деле, и абсолютные величины членов ряда образуют убывающую последовательность:

.

При имеем . Этот ряд расходится. Следовательно, областью сходимости данного ряда является полуинтервал [-1,1).

б) Радиус сходимости найдём по формуле

.

Здесь . Тогда .

В данном примере , поэтом интервалом сходимости ряда будет (5/2,7/2).

Исследуем поведение ряда на концах интервала сходимости.

Положив , получим ряд

А при – ряд

.

Оба ряда расходятся, так как не выполняется необходимое условие сходимости ряда. В первом случае не существует, а во втором

3 Найти , если .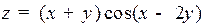

Решение

Используем формулу третьего дифференциала

Производные первого порядка:

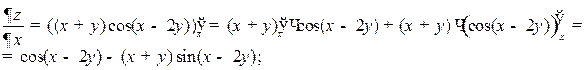
Производные второго порядка:

Производные третьего порядка:

Подставляя вычисленные производные в формулу дифференциала, получим:

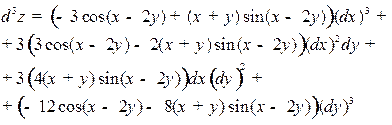
4 Представить в тригонометрической и показательной форме число .

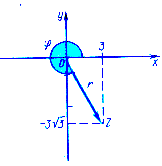
Рисунок 3

Решение

Так как а=3, , то

.

Геометрически определяем, что числу z соответствует точка Z, лежащая в IV четверти, (рисунок 3).

Составим отношения

cosφ=a/r=3/6=1/2, .

Отсюда следует, что φ=360º-60º=300º или . Значит, r=6, . Итак, 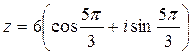- тригонометрическая форма, а - показательная форма данного числа.

5 Найти аналитическую функцию f(z), если известна ее мнимая часть .

Решение

Поскольку то из равенств

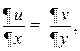
получаем:

Из первого уравнения находим

,

где φ(y) – произвольная функция. Для определения функции φ(y) продифференцируем по у функцию u=-4x+φ(y) и подставим полученную производную во второе уравнение: -4x+φ(y)=-4х-1, откуда φ(y)=-у+С. Следовательно, u=-4xy-y+C, поэтому

где z=x+iy.

6 Найти общий интеграл уравнения:

а) (x²+2xy)dx + xydy = 0; б) .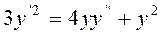

Решение

а) Здесь H(x,y)=x²+2xy, Q(x,y)=xy. Обе функции – однородные второго измерения.

Введем подстановку y=tx, откуда dy=xdt+tdx. Тогда уравнение примет вид

(x²+2x²t)dx+tx²(xdt+tdx)=0, или (x²+2x²t+t²x²)dx+tx³dt=0.

Разделяя переменные и интегрируя, имеем

; .

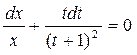Преобразуем второй интеграл:

, или .

Возвращаясь к прежней неизвестной функции y (t=y/x), получаем окончательный ответ:

.

б) Разделим обе части уравнения на y²:

.

Положим , откуда , или . В результате получим уравнение

3z²-4z²-4z^’=1, или -4z^’=1+z², т.е. .

Отсюда, интегрируя, находим

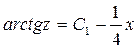, или , или .

Интегрируя последнее уравнение, получим

, или .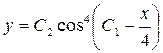

7 Дана матрица

.

Построить орграф, для которого данная матрица является матрицей смежности. Найти матрицу инцидентности орграфа.

Решение

Для построения орграфа его вершине однозначно сопоставим точку на плоскости. Данная матрица смежности имеет четыре строки и четыре столбца, следовательно, в орграфе четыре вершины: 1, 2, 3, 4.

Рисунок 4

Проанализируем элементы матрицы:

- при вершине 1 нет петель;

- из вершины 1 выходят две стрелки к вершине 2;

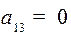- из 1 не выходит ни одной стрелки к вершине 3;

- из 1 не выходит ни одной стрелки к вершине 4;

- из 2 не выходит ни одной стрелки к вершине 1;

- при 2 нет петель;

- из 2 выходит одна стрелка к вершине 3;

- из 2 не выходит ни одной стрелки к вершине 4;

- из 3 выходит одна стрелка к вершине 1;

- из 3 не выходит ни одной стрелки к вершине 2;

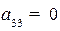- при 3 нет петель;

- из 3 выходит одна стрелка к вершине 4;

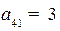- из 4 выходит 3 стрелки к вершине 1;

- из 4 выходит одна стрелка к вершине 2;

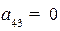- из 4 не выходит ни одной стрелки к вершине 3;

- при 4 нет петель.

Строим орграф, (рисунок 4)

Для построенного орграфа запишем матрицу инцидентности:

Здесь четыре строки по числу вершин и 9 столбцов по числу дуг.

8 Методом половинного деления найти корни уравнения с точностью до

Решение

Поскольку при то очевидно, что на отрезке находится единственный действительный корень данного уравнения.

Чтобы уточнить искомый корень уравнения методом половинного деления, составим следующую таблицу 3:

Таблица 3

					Знаки функции
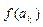
	0,5 0,5 0,625 0,625 0,656 0,672 0,68 0,68 0,682 0,682	0,75 0,75 0,688 0,688 0,688 0,688 0,684 0,684 0,683	0,5 0,75 0,625 0,6875 0,6565 0,672 0,68 0,684 0,682 0,683 0,6825	–0,375 0,171875 –0,13085… 0,01245… –0,06055… –0,02453… –0,005568 0,00401… –0,00078… 0,00161…	– – – – – – – – – –	– + – + – – – + – +	+ + + + + + + + + +

Поскольку то требуемая точность вычислений достигнута. Следовательно,

Дата добавления: 2015-07-11