Основы стохастической теории тестов (IRT)

В 80-х гг. XX в. в психологических и педагогических измерениях получили широкое развитие методы современной теории тестов Item Response Theory (в буквальном переводе, теория «задание-ответ»), сокращенно IRT. В целом IRT предназначена для оценивания латентных (ненаблюдаемых) параметров испытуемых и заданий тестов на основе математико-статистических моделей измерения и является частью более общей теории латентно-структурного анализа. Особенно эффективной оказывается данная теория при разработке тестов достижений (педагогических тестов).

В основе теории «Задание-ответ» лежит тот факт, что зависимость вероятности решения задания (P) от выраженности у испытуемого соответствующей способности (θ) хорошо описывается логистической функцией, которая имеет такой вид:

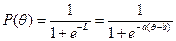, где e = 2,718.

Параметр функции 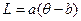называется логит.

Основной моделью в IRT является двухпараметрическая модель А. Бирнбаума, которая является непосредственным приложением логистической функции к анализу тестовых заданий.

Двухпараметрическая модель Бирнбаума выражается формулой:

,

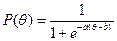где b – параметр трудности задания (трудность), θ – способность испытуемого, a – параметр дискриминативности (дискриминативность) задания.

Существенно, что латентные (скрытые) параметры θ (способность) и b (трудность) изначально оцениваются в одной и той же шкале: интервальной шкале логитов, хотя для удобства практического использования теста от шкалы логитов переходят к более привычным шкалам.

Если пренебречь различиями в дискриминативности заданий и считать параметр дискриминативности равным единице, то получается однопараметрическая модель Г. Раша:

,

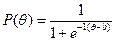где b – параметр трудности задания (трудность), θ – способность испытуемого.

В.Н. Дружинин отмечает, что если рассматривать значение параметра θ_i, как положение i -го испытуемого на шкале логитов, а значение b_j, – как положение j -го задания на той же шкале, то разность параметров получает интересную геометрическую интерпретацию. Абсолютная величина разности θ_i – b_j – это расстояние, на котором находится испытуемый с уровнем подготовки θ, от задания с трудностью b. Если эта разность велика по модулю и отрицательна, то задание бесполезно для измерения уровня подготовленности i -го ученика, поскольку он наверняка не сможет выполнить такое трудное задание верно.

Большие положительные значения этой разности тоже не представляют интереса ни для процесса контроля, ни для обучения i -го испытуемого, поскольку они говорят о том, что задания такой трудности давно освоены учащимся и он справится с ними успешно при выполнении теста. Такие задания неэффективны для оценивания данного значения θ (способности). Наименьшую ошибку измерения обеспечивают задания, трудность которых приблизительно равна уровню подготовленности испытуемого, т. е. задания, подобранные по критерию θ ≈ b. На основе данной теории можно разработать весьма эффективный тест и построить шкалу, позволяющую точно оценить выраженность измеряемого свойства.

В ходе разработки теста для каждого из заданий на основе эмпирических данных оцениваются параметры дискриминативности (a) и трудности (b). С целью наглядного представления и оценки качества заданий строят характеристические кривые заданий, которые отражают зависимость вероятности решения задания от способности испытуемого. Форма этих кривых полностью определяется параметрами заданий (a и b).

На основе анализа характеристических кривых и параметров заданий для итогового теста отбирают задания с наиболее желательными характеристиками (например, с высоким уровнем трудности, если составляется тест для выявления наиболее одаренных детей). На основе параметров отдельных заданий можно оценить параметры теста и построить его характеристическую кривую.

Рассмотрим для примера характеристические кривые заданий с разными значениями коэффициентов дискриминативности (a) и трудности (b). На рисунке 1 приведены характеристические значения трех заданий с разными значениями коэффициента дискриминативности (a). Из анализа графика становится ясно, что задание с большим по модулю значением дискриминативности (-2) демонстрирует наибольшую различительную способность в области средних значений (θ) – здесь кривая нарастает с наибольшей крутизной и небольшой прирост измеряемого свойства существенно увеличивает вероятность решения. Такое задание хорошо подходит для тех случаев, когда необходимо провести диагностику испытуемых с выраженностью диагностируемого свойства близкой к средней. В случае высокой или низкой такое задание менее эффективно. В то же время задание с наименьшим абсолютным значением коэффициента дискриминативности (-0,5) плохо различает испытуемых имеющих примерно равные значения выраженности признака в области средних значений – значительный прирост способности довольно слабо увеличивает вероятность решения задания.

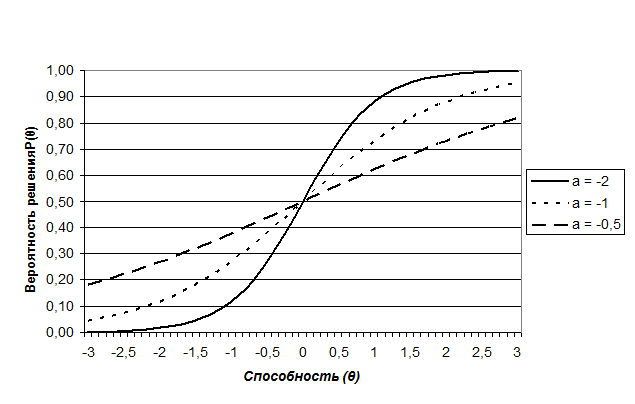Рис. 1. Пример характеристических кривых заданий с разными значениями
коэффициента дискриминативности (a)

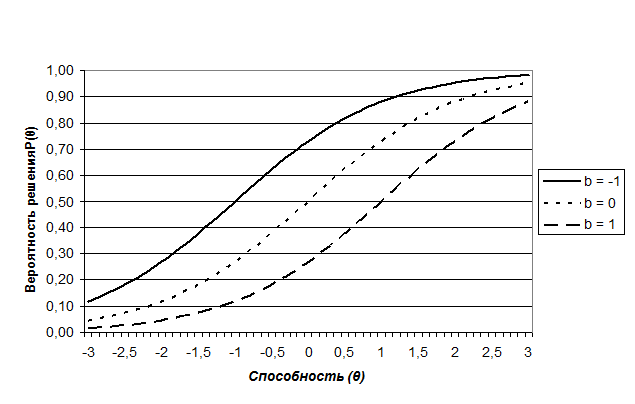Рис. 2. Пример характеристических кривых заданий с разными значениями
коэффициента трудности (b)

Кривые заданий с разными значениями коэффициента трудности (рисунок 2) легко интерпретировать, если обратить внимание на то, при каком уровне измеряемого свойства (способности) вероятность решения составит 0,5. Очевидно, что наиболее трудным является задание с коэффициентом b равным 1, поскольку в этом случае такая вероятность решения требует наибольшей способности от испытуемого. И, наоборот, задание с коэффиентом b равным -1, имеет наименьшую трудность.

Таким образом, на основе теории «Задание-ответ» можно построить тест с желаемыми параметрами трудности и дискриминативности. Это особенно полезно при составлении тестов интеллекта и умственного развития, тестов достижений, выявляющих уровень обученности испытуемых (педагогических тестов). Некоторые модели IRT использовались отечественными учеными при разработке теоретических и методических основ единого государственного экзамена (ЕГЭ).

Использование данной теории при конструировании личностных тестов пока весьма ограничено, хотя удачные примеры подобного рода за рубежом существуют (например, тест «Переживания в межличностных отношениях» C. Fraley, направленный на оценку стиля привязанности).

Многие авторы, в частности Пол Клайн, отмечают, что IRT обладает множеством недостатков: вычислительные трудности, требующие использования специальных компьютерных программ, трудоемкость при разработке. Например, для того чтобы получить надежную и не зависимую от испытуемых шкалу свойств, требуется провести тестирование очень большой выборки (не менее 1000 испытуемых).

По мнению В.Н. Дружинина, главным недостатком IRT является игнорирование проблемы валидности. Он подчеркивает, что в психологической практике не наблюдается случаев, когда ответы на задания теста были бы обусловлены лишь одним фактором.

Тем не менее, опыт применения данной теории показывает, что разработанные с её помощью тесты являются, как правило, весьма валидными и надежными, не уступая методикам, основанным на классической эмпирико-статистической теории.

Дата добавления: 2015-07-10