Метод линейной стандартизации.

Этот метод обычно используется в тех случаях, когда распределение сырых баллов соответствует нормальному. Напомним из курса математической статистики, что нормальное распределение является хорошим приближением распределения большого числа наблюдений, которые зависят от множества независимых факторов. Поскольку многие психические свойства в своих проявлениях действительно зависят от множества независимых факторов, закон нормального распределения широко применяется в психологических исследованиях.

Нормальное распределение обладает многими преимуществами, в частности оно позволяет заранее рассчитать, сколько случаев будет расположено в определенном удалении от средней арифметической (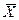) при использовании для определения удаленности стандартного отклонения (σ). Для этого имеются специальные таблицы. Из них видно, что в пределах 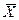±σ находится 68% изучаемых случаев. За этими пределами находится 32% случаев, а так как распределение симметрично, то по 16% с каждой стороны. В диапазон 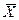±3σ попадает более 99% наблюдений. Известная из закона нормального распределения связь значний признака с его частотой (или вероятностью) используется в нелинейной стандартизации тестов. Линейная стандартизация выполняется ещё проще с использованием элементарных линейных преобразований исходной шкалы сырых баллов. Эти преобразования всего лишь меняют точку начала отсчета и масштаб шкалы.

Эти преобразования можно разбить на два этапа. Сначала осуществляется переход от сырых баллов к стандартизованным оценкам (выраженным в масштабе единичного нормального распределения со средним M = 0 и стандартным отклонением σ = 1) по формуле:

,

В этой формуле zi – стандартизованная оценка для i -того испытуемого, xi – оценка того же испытуемого в сырых баллах, – среднее шкалы сырых баллов в выборке стандартизации, Sx – стандартное отклонение шкалы сырых баллов.

Стандартизованные оценки удобны тем, что от них легко можно перейти к любой стандартной шкале распространенной в психологической диагностике: шкале стэнов, шкале станайнов, шкале Т-оценок и т.д. Поэтому на втором этапе осуществляется переход к произвольной шкале (с тем средним и стандартным отклонением, которые желает получить психолог) с помощью формулы:

,

где yi – оценка i -того испытуемого в некоторой стандартной шкале (например, шкале стэнов), zi – стандартизованная оценка для i -того испытуемого, M – среднее значение выбранной стандартной шкалы, s – стандартное отклонение данной шкалы.

Из последней формулы ясно, что всего две величины – среднее значение M и стандартное отклонение s – задают стандартную шкалу, определяя точку начала отсчета и её масштаб. Эти величины могут быть выбраны произвольно, однако чаще всего используется одна из традиционных шкал с привычными для психологов значениями M и s. К их числу можно отнести следующие стандартные шкалы:

1. Шкала IQ (М = 100, s = 15). Пример: тест Векслера.

2. Т-шкала Маккола (М = 50, s = 10). Эта шкала представляет собой стандарт Американской психологической ассоциации. Пример: Миннесотский многоаспектный личностный опросник (MMPI).

3. Шкала стенов (М = 5,5; s = 2). Пример: Шестнадцатифакторный личностный опросник Кэттелла (16PF).

4. Шкала станайнов (М = 5, s = 2). Пример: Фрайбургский личностный опросник (FPI).

Так, например, в русской адаптации теста MMPI, которая называется стандартизированный многофакторный метод исследования личности (СМИЛ) используется Т-шкала Маккола. Соответственно, переход от сырых баллов к стандартным оценкам для каждой шкалы СМИЛ осуществляется по формуле:

.

Здесь xi – сырые баллы полученные испытуемым по некоторой шкале, 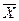– среднее значение по данной шкале, полученное на выборке стандартизации и приведенное в руководстве к тесту, S - стандартное отклонение по данной шкале, полученное на выборке стандартизации, 50 – среднее значение Т-шкалы, 10 – стандартное отклонение Т-шкалы. Чтобы воспользоваться этой формулой для перевода сырых баллов в стандартные достаточно знать (среднее шкалы сырых баллов в выборке стандартизации) и S (стандартное отклонение шкалы сырых баллов в выборке стандартизации), которые должны быть приведены в руководстве к тесту.

Таким образом, в простейшем случае, для осуществления линейной стандартизации теста достаточно провести тест на выборке стандартизации, рассчитать средние значения и стандартные отклонения для разных половозрастных групп, выбрать стандартную шкалу с общепринятыми значениями М и s и привести все эти данные в руководстве к тесту. Если это выполнено, то психолог, использующий тест сможет самостоятельно перейти от сырых баллов испытуемых к стандартным. Однако, ввиду сложности вычислений для упрощения перевода сырых баллов в шкальные оценки разрабатываются так называемые конверсионные таблицы.

Конверсионные таблицы составляются для разных половозрастных групп и показывают соответствие сырых баллов стандартным. Если предполагается разработка конверсионной таблицы, то разумно выбрать такую стандартную шкалу, размах которой значительно меньше размаха сырых баллов. По этой причине, на практике чаще всего выбирают шкалу стэнов и шкалу станайнов.

Рассмотрим разработку конверсионной таблицы методом линейной стандартизации на примере. Предположим, что некоторый новый опросник опросник из 20 вопросов был проведен на выборке из 80 испытуемых юношей 18-22 лет. Составим конверсионную таблицу, позволяющую перейти от сырых баллов к стэнам. В ходе обработки результатов диагностики было установлено, что среднее значение в шкале сырых баллов = 10; стандартное отклонение S = 5,5. Запишем в первый столбец таблицы все возможные значения в шкале сырых баллов (см. табл. 1).

Таблица 1

Сырые баллы	xi -	Zi	2´Zi	5,5+2´Zi	Стэн
	-10	-1,82	-3,64	1,86
	-9	-1,64	-3,27	2,23
	-8	-1,45	-2,91	2,59
	-7	-1,27	-2,55	2,95
	-6	-1,09	-2,18	3,32
	-5	-0,91	-1,82	3,68
	-4	-0,73	-1,45	4,05
	-3	-0,55	-1,09	4,41
	-2	-0,36	-0,73	4,77
	-1	-0,18	-0,36	5,14
		0,00	0,00	5,50
		0,18	0,36	5,86
		0,36	0,73	6,23
		0,55	1,09	6,59
		0,73	1,45	6,95
		0,91	1,82	7,32
		1,09	2,18	7,68
		1,27	2,55	8,05
		1,45	2,91	8,41
		1,64	3,27	8,77
		1,82	3,64	9,14

Для каждого значения рассчитаем разность xi- 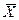( второй столбец) и, чтобы получить Zi разделим полученные разности на S (третий столбец). Чтобы перейти к стэнам умножим каждое значение zi на стандартное отклонение в шкале стэнов, т.е. на 2 (четвертый столбец). Прибавив к полученным значениям 5,5 (среднее в шкале стэнов) и округлив до целых, мы перейдем стэнам. Для удобства значения сырых баллов соответствующие одному и тому же стэну следует сгруппировать. Итоговая конверсионная таблица представлена в табл. 2.

Таблица 2

Сырые баллы	Стэн
0 - 1
2 - 4
5 - 7
8 - 9
10 - 12
13 - 15
16 - 18
19 - 20

Описанный выше способ стандартизации является универсальным, т.е. применимым для любых стандартных шкал. В том случае, если в качестве стандартной шкалы выбрана шкала стэнов процедуру составления конверсионной таблицы можно упростить. Известно, что один стэн охватывает интервал соответствующий половине стандартного отклонения (т.е. 0,5S), а нижняя граница шестого стэна (равная 5,5) соответствует среднему выборочному значению в шкале сырых баллов. Это значит, что для определения нижней границы седьмого стэна (и, одновременно, верхней границы шестого) необходимо к среднему прибавить половину стандартного отклонения. Для предыдущего примера она составит 10 + 0,5´5,5 = 12,75. Это значит, что в шестой стэн попадают значения от 10 и до 12,75. В этот интервал попадает три возможных значения шкалы сырых баллов: 10, 11 и 12.

Верхняя граница седьмого стэна (и нижняя граница восьмого стэна) вычисляется прибавлением к его нижней границе 0,5S, т.е., в нашем случае, 12,75 + 0,5´5,5 = 15,5. Это значит, что в седьмой стэн попадут значения 13, 14 и 15. Верхняя граница восьмого стэна равна 15,5 + 0,5´5,5 = 18,25, т.е. в него попадают значения 16, 17 и 18. Верхняя граница девятого стэна равна 18,25 + 0,5´5,5 = 21 и в него попадают значения 19 и 20.

Определить нижнюю границу пятого, четвертого и др. стэнов можно путем вычитания 0,5S от границы следующего по величине стэна. Рассчитаем эти границы для нашего примера. Для пятого стэна она равна 10-0,5´5,5 = 7,25, т.е. в него попадают значения 8 и 9. Для четвёртого – 7,25-0,5´5,5 = 4,5, в него попадают значения 5, 6 и 7. Для третьего стэна – 4,5-0,5´5,5 = 1,75. В этот стэн попадают значения 2, 3, 4. Второй стэн имеет нижнюю границу, равную 1,75-0,5´5,5 = -1. В него попадают два значения сырых баллов – 0 и 1.

Таким образом, мы рассчитали границы каждого стэна, которые можно было бы свести в общую таблицу. Эта таблица окажется полностью идентичной таблице 2, которую мы получили применяя другой способ линейной стандартизации.

Дата добавления: 2015-07-10