Основы классической эмпирико-статистической теории теста

В основе эмпирико-статистической теории теста лежит классическая теория погрешности измерений, заимствованная из естественных наук. В рамках этой теории считается, что тест — такой же измерительный прибор, как вольтметр, термометр или барометр, и результаты, которые он показывает, зависят от величины свойства у испытуемого, а также от самой процедуры измерения («качества» прибора, действий экспериментатора, внешних помех и т.д.). Иными словами, данная теория основана на предположении о принципиальном сходстве психологического и физического измерения, упрощающем реальную сложность измерения в психологии.

Изначально по аналогии с измерением в естественных науках подразумевалось, что…

· измеряемые свойства стабильны, неизменны с течением времени и имеют некоторое постоянное «истинное значение»;

· измеряемые свойства не зависят от измерительных средств (приборов, тестов и пр.);

· измеряемые свойства не зависят от исследователя, проводящего измерения.

Эти предположения плохо соотвествуют реальности психологического измерения, что вызывает оправданную критику данной теории. Кроме этих «фундаментальных» предположений в классической теории есть также ряд допущений математико-статистического порядка, которые также далеко не всегда выполняются в реальности:

· измеряемое психическое свойство считается линейным и одномерным;

· оценка психологических свойств и состояний с помощью тестов осуществляется на шкале интервалов;

· распределение совокупности людей, обладающих данным свойством, описывается кривой нормального распределения.

На самом деле, существует немало психологических свойств, распределение которых не соответствует нормальному, результаты тестов лишь с большой натяжкой можно признать интервальными измерениями, а одномерность и линейность свойств доказать очень сложно. Тем не менее, психологи на практике ведут себя так, как будто эти допущения всегда выполняются.

Предполагается, что любое измеряемое свойство имеет истинный показатель, а показания по тесту отклоняются от истинного на величину случайной погрешности. На показания теста влияет и систематическая погрешность, но она сводится к прибавлению (вычитанию) константы к истинной величине параметра каждого испытуемого, что для интерпретации результатов значения не имеет.

Основной задачей, которую ставит и решает классическая теория теста является контроль над такими ошибками (погрешностями) и сведение их к минимуму.

Количественной мерой случайной погрешности измерения является величина, которая называется «Стандартная погрешность измерения» или «Стандартная ошибка оценки». Стандартная ошибка оценки (S_e) характеризует величину интервала вокруг значения оценки, в который с заданной вероятностью попадает истинное значение свойства (t).

Так, например, известно, что для «Теста Векслера для детей» значение S_e лежит в пределах 3,36-4,25. Если для точности взять значение 3,36, то можно сказать, что истинное значение коэффициента интеллекта с вероятностью 95% лежит в пределах: X ± 7 баллов, где X – это оценка, полученная испытуемым в ходе тестирования.

Чтобы определить границы интервала, в который с вероятностью 95% попадает истинное значение необходимо к оценке, полученной при тестировании прибавить и отнять 1,96 S_e. Графически это можно проиллюстрировать с помощью числовой прямой, как на рисунке ниже:

Продемонстрируем расчеты доверительного интервала истинного значения для приведенного выше примера с тестом Векслера. Если S_e = 3,36, то 1,96 x 3,36 = 6,59 ≈ 7. Следовательно коэффициент интеллекта с вероятностью 95% лежит в пределах X ± 7 баллов, где X – это оценка, полученная испытуемым в ходе тестирования.

Так, если испытуемый В. Сидоров получил 112 баллов по тесту, то при повторном тестировании его результат с высокой вероятностью будет лежать в пределах от 105 (т.е. 112-7) до 119 (112+7).

С математической точки зрения стандартная ошибка оценки (S_e) представляет собой стандартное отклонение показателей, полученных при многократном повторном измерении свойства одного и того же испытуемого. На практике значение стандартной ошибки оценки может быть вычислено на основе её связи с надежностью теста.

Надежность характеризует устойчивость результатов теста при повторном тестировании и оценивается путем вычисления меры связи (коэффициента корреляции) между результатами первого и повторного тестирования одних и тех же испытуемых.

Связь стандартной ошибки оценки с надежностью теста отражает формула:

,

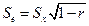где S_x – стандартное отклонение по тесту, r – коэффициент надежности. Следовательно, чем выше коэффициент надежности, тем меньше стандартная ошибка оценки и, следовательно, ниже погрешность измерения. По существу, надежность выступает как альтернативный способ оценки погрешности измерения.

Другой важнейшей характеристикой теста, определяющей с точки зрения классической теории погрешность измерений, является валидность. Валидность означает пригодность теста измерять то свойство, для измерения которого он предназначен. Следовательно, чем больше на результат выполнения теста или отдельного задания влияет измеряемое свойство и чем меньше – другие переменные, тем тест валидней.

Соотношение надежности и валидности теста характеризуется «основным психометрическим законом»: валидность теста не может быть больше его надежности. Поэтому, при разработке нового теста, сначала необходимо убедиться в его надежности, и лишь затем – проверять его валидность. Ненадежный тест не может валидно измерять ни одно свойство.

С точки зрения классической эмприко-статистической теории теста задания сравнительно однородны, следовательно, результаты выполнения разных заданий можно суммировать с учетом весовых коэффициентов. Так получается «сырой» балл, который можно привести к любой стандартной шкале, используя различные способы стандартизации.

Таким образом, классическая эмпирико-статистическая теория теста нацеливает психолога на разработку стандартизированных, надежных и валидных тестов, имеющих минимальную погрешность измерения.

Дата добавления: 2015-07-10