Основные понятия

Cаратовский государственный технический университет

Определение удельного заряда электрона методом магнетрона

Методические указания

к выполнению лабораторной работы по физике

для студентов всех специальностей

всех форм обучения

Электронное издание локального распространения

Одобрено

редакционно-издательским советом

Саратовского государственного

технического университета

САРАТОВ-2006

Все права на размножение и распространение в любой форме остаются за разработчиком.

Нелегальное копирование и использование данного продукта запрещено.

Составители - Зюрюкин Юрий Анатольевич, Сысоев Виктор Владимирович

Рецензент - Задорожный Филлип Михайлович

410054, Саратов, ул. Политехническая 77,

Научно-техническая библиотека СГТУ,

тел. 52-63-81, 52-56-01

http://lib.sstu.ru

Регистрационный

номер 060568Э

© Саратовский государственный

технический университет 2006 г.

Цель работы: определить удельный заряд электрона по сбросовым характеристикам электрического тока в цилиндрическом магнетронном диоде и проверить наличие параболы критического режима.

ОСНОВНЫЕ ПОНЯТИЯ

Электрон является одной из самых легких элементарных частиц. Масса электрона составляет (9,1085±0,0006)· 10^-31 кг. Заряд электрона является условно отрицательным и наименьшим электрическим зарядом, часто называемым элементарным. Все другие электрические заряды являются кратными по отношению к заряду электрона.

Впервые электрон был открыт при изучении катодных лучей в катодных трубках в 1895 г., а его заряд был определен в 1911 г. Отношение заряда электрона e к его массе m_e (e/m_e) называется удельным зарядом электрона.

Удельный заряд электрона можно оценить путем изучения движения электрона в скрещенных электрических и магнитных полях, с помощью, например, магнетрона.

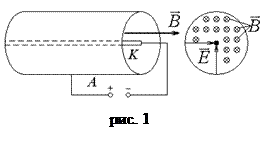Магнетрон представляет собой двухэлектродную вакуумную лампу (диод), в которой один из электродов служит для эмиссии (испускания) электронов (нагреваемый катод), а другой является анодом. В качестве магнетрона удобнее всего использовать диод, имеющий цилиндрический анод А и нитевидный катод К, расположенный по оси анода (рис. 1), что и применено в работе. Диод помещен в аксиальное, т.е. направленное вдоль оси анода, магнитное поле[1]. При такой конфигурации электрическое и магнитные поля взаимно перпендикулярны (см. рис.1).

При отсутствии магнитного поля (т.е. когда ток в соленоиде равен нулю) электроны, испускаемые вследствие термоэлектронной эмиссии из катода, под действием электрического поля движутся прямолинейно от катода к аноду по направлению действия силы электрического поля , т.е. по радиусам (см. рис. 3). Соответственно, в анодной цепи возникает некоторый ток, величина которого определяется током накала катода (или, другими словами, нагревом катода) и значением анодного напряжения. Если, не меняя ток накала катода и анодное напряжение, приложить некоторое магнитное поле (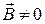), что достигается пропусканием электрического тока через соленоид, то на электрон будет действовать сила Лоренца

,

(1)

где - скорость электрона, –вектор магнитной индукции.

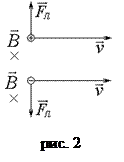В соответствии с (1) направление действия силы Лоренца определяется как результат векторного произведения векторов и . Иногда для ее определения легче запомнить правило «левой руки»: если направить пальцы (кроме большого) по направлению движения положительного заряда так, чтобы вектор “входил” в ладонь, то отогнутый большой палец покажет направление силы Лоренца (Рис. 2). Так как электрон имеет отрицательный заряд, пальцы нужно направлять в направлении, противоположном направлению его скорости.

Следует отметить, что направление силы Лоренца всегда перпендикулярно перемещению заряженной частицы и, поэтому, эта сила работы не совершает. Сила Лоренца влияет только на направление скорости частицы и, соответственно, на траекторию ее движения.

В рассматриваемом магнетроне, вектор скорости движения электрона лежит в плоскости сечения диода, а вектор индукции магнитного поля направлен вдоль оси цилиндра. Поэтому векторы и являются взаимно перпендикулярными и величина силы Лоренца равна

,

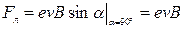(1а)

где v и B – модули соответствующих векторов, α – угол между векторами и .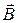

Таким образом, при наличии магнитного поля на движение электрона в магнетроне влияют две силы: сила электрического поля и сила, действующая со стороны магнитного поля, 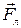. Поэтому, в соответствии со вторым законом Ньютона уравнение движения электрона будет определяться следующим соотношением:

,

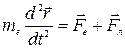(2)

где r - радиус-вектор перемещения электрона.

Из-за действия магнитного поля, траектория движения электронов становится не прямой, как в случае приложения только электрического поля, а криволинейной (Рис. 3). Однако при сравнительно небольших магнитных полях, несмотря на искривление траектории, все электроны, вылетевшие из катода, попадут на анод (Рис. 3, случай (b)).

Поэтому при небольшой величине магнитного поля, в анодной цепи будет протекать практически такой же ток I_a, как и в отсутствие магнитного поля. Но, если увеличивать величину магнитного поля (при увеличении тока, протекающего по соленоиду I_c), траектории движения электронов будут все больше искривляться. При некотором значении B_кр (при силе тока в соленоиде I_c^кр), называемом критическим магнитным полем, электроны будут перемещаться по дуге вблизи анода без попадания на него и возвращаться на катод (Рис. 3, случай (с)). В результате, при В=В_кр анодный ток должен снизиться до нуля. При дальнейшем росте I_c и увеличении B, траектории электронов будут все больше искривляться (Рис. 3, случай (d)) и последние не будут долетать до анода. Следовательно, анодный ток будет оставаться равным 0.

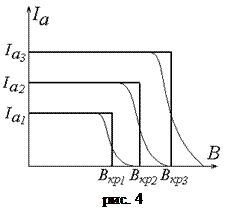Зависимость анодного тока I_a от величины индукции магнитного поля B при постоянном напряжении и постоянном токе накала катода называется сбросовой характеристикой магнетрона. На Рис. 4 показаны сбросовые характеристики магнетрона для различных значений анодного тока I_a. Вертикальное уменьшение анодного тока до нуля при В=В_кр справедливо только для одного электрона или группы электронов, имеющих равные скорости. Так как электроны, вылетающие из катода, имеют, в действительности, различные скорости, то критические значения магнитного поля для них различаются. В результате, экспериментальная зависимость I_a(B) имеет вид как показано на Рис. 4 тонкими линиями.

Критическое значение магнитного поля является некоторой функцией от анодного напряжения: 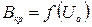, причем с увеличением анодного напряжения увеличивается значение B_кр.

Для решения задачи определения удельного заряда электрона мы ограничимся рассмотрением движения электрона при приложении критического магнитного поля[2]. В этом случае, повторим, электрон перемещается по некоторой криволинейной траектории, проходящей вблизи анода. В верхней части траектории движение электрона можно рассматривать как движение по некоторой окружности. В качестве допущения будем считать, что радиус этой окружности равен половине радиуса цилиндрического анода r_a (см. Рис. 3(с))[3]:

.

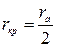(3)

Как было уже отмечено, на движение электрона оказывают влияние две силы: сила электрического поля и сила Лоренца. Векторная сумма этих двух сил определяет центростремительное ускорение (действующее по направлению, перпендикулярному траектории, к центру окружности). На Рис. 5 изображены вектора сил электрического поля и силы Лоренца в верхней части траектории движения электрона. Обе эти силы направлены по радиусу, но в разные стороны. То есть суммарная центростремительная сила, действующая в верхней части траектории движения электрона, будет равна разности величин этих двух сил:

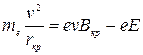
(4)

или с учетом (3)

,

(5)

где напряженность электрического поля Е вблизи анода может быть определена через разность потенциалов между анодом и катодом U_a приближенно по формуле плоского конденсатора:

.

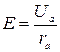(6)

Как уже отмечалось, величина скорости электрона изменяется только под действием силы электрического поля. Поэтому, чтобы оценить скорость электрона v вблизи анода, отметим, что при перемещении электрона от катода к аноду электрическое поле совершит работу

.

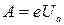(7)

Эта работа будет затрачена на изменение кинетической энергии электрона

.

(8)

Согласно закону сохранения энергии, приравняем правые части выражений (7) и (8):

,

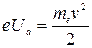(8)

откуда

.

(9)

Подставляя выражения (9) и (6) в формулу (5) после несложных преобразований получим

.

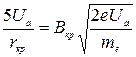(10)

Возводя в квадрат обе части выражения (10) выразим удельный заряд электрона

.

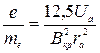(11)

Более строгий учет фактического радиуса кривизны траектории движения электрона вблизи анода в режиме критического магнитного поля приводит к формуле, отличающейся от (11) только численным коэффициентом[4]:

.

(12)

В данной работе для создания магнитного поля применяется соленоид, диаметр витков которого значительно меньше его длины. Это позволяет считать его бесконечно длинным и при расчетах использовать формулу, связывающую индукцию магнитного поля с током I_c, справедливую для соленоидов такого типа:

,

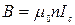(13)

где µ₀ – магнитная постоянная (= 1.26·10^-6 Гн/м), n – число витков соленоида, приходящееся на один метр (указано на измерительном стенде). Тогда величина критического магнитного поля будет равна

.

(14)

Подставляя выражение (14) в (12), получим

.

(15)

Величины μ₀, n, r_a – являются постоянными для данной экспериментальной установки. Поэтому можно ввести обозначение

,

(16)

с учетом которого выражение (15) примет вид

.

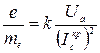(17)

Полученное выражение (17) является рабочей формулой, используемой для экспериментального определения удельного заряда электрона в данной работе.

Отметим, что из соотношения (17) можно получить выражение, отражающее собой так называемую параболу критического режима магнетрона, как функцию U_a от I_c^кр:

.

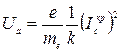(18)

При анализе зависимости (18) значения e/m_e и k считаются уже известными.

Дата добавления: 2015-10-21