Приложение. В 1922-1923 гг. американский физик Артур Комптон, исследуя рассеяние рентгеновского

В 1922-1923 гг. американский физик Артур Комптон, исследуя рассеяние рентгеновского излучения на легких элементах, установил, что рассеянное излу­чение, наряду с излучением первоначальной длины волны , содержит также излучение с большей длиной волны . Разность зависела только от угла рассеяния между направлением рассеянного рентгеновского излучения и первоначальным пучком, не испытавшим рассеяния. Явление получило назва­ние эффекта Комптона.

Детально изученное Комптоном появления смещенной компоненты в спектре рассеяния рентгеновского излучения, объясняется в предположении, что излучение имеет чисто корпускулярную, квантовую природу т.е., представляет собой поток фотонов, обладающих энергией hν. Рассеяние рентгеновских лучей на свободных (или слабо связанных) электронах вещества, с появлением компоненты излучения, смещенной относительно длины волны первичного излучения, в сторону увеличения, интерпретируется как результат абсолютно упругого соударения двух частиц - электрона и фотона, обладающих определенными энергией и импульсом.

Заметим, что комптоновское рассеяние может происходить не только на электроне, но и на любой частице, способной взаимодействовать с электромагнитным излучением. При этом все формулы, основанные на законе сохранения, остаются справедливыми (с заменой m на массу покоя рассматриваемой частицы).

Представим пове­дение электрона в волне. Если электрон вначале был свободен и покоился, то под действием волны он начинает колебаться и, будучи электрически заряжен­ной частицей, сам начинает испускать электромагнитное излучение. Если бы этот электрический диполь оставался на месте, то он излучал бы волну с той же частотой, что и падающая волна. Однако световое давление заставляет дви­гаться с ускорением свободный электрон. В этом случае внешнее излучение как бы догоняет двигающийся электрон и относительно него рассеивающая волна имеет большую длину волны

Расчет доплеровского смещения для этого слу­чая приводит к формуле

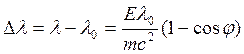(2)

где E - энергия, полученная от падающего света, m - масса электрона, c -скорость света,

а - угол, под которым находится наблюдатель относительно направления первоначального пучка света.

Как видно, эта формула содержит наблюдаемую в опыте Комптона зави­симость от угла . Однако, в отличие от установленного в эксперименте факта постоянства величины для данного угла , согласно формуле (2) должна постоянно возрастать со временем, поскольку частица получает энергию и, кроме того, должна зависеть от интенсивности падающей вол­ны, поскольку от нее зависит сила давления, а следовательно и скорость элек­трона.

Указанные противоречия были разрешены Комптоном, когда он в модели взаимодействия рассмотрел электромагнитное излучение как поток частиц (фотонов или квантов излуче­ния), обладающих импульсом

, (3)

(где - волновой вектор, - частота падающего излучения, - постоянная Планка = эВ с) и энергией

(4)

Поскольку, Комптон – эффект становится заметным, когда энергия фотонов 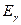значительно больше средней энергии электрона в атоме, то комптоновское рассеяние можно рассматривать, как упругое столкновение двух шаров - фотона и свободного электрона, при условии, что начальная скорость электрона равна нулю. В этом случае энергия электрона до столкновения равна m₀c² (m₀ - мас­са покоя электрона), а его импульс равен нулю. После столкновения (рис.1)

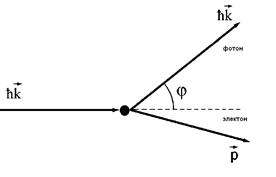
Рис. 1. Схема рассеяния фотона на свободном электроне

импульс электрона изменится и станет равным (нерелятивистский случай), а его полная энергия (кинетическая энергия плюс энергия покоя) будет равна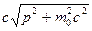

Из законов сохранения энергии и импульса следует

(5)

(6)

Где и - частота и вектор рассеянного излучения.

,

Откуда получаем

,

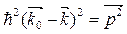
Приравнивая левые части, получим

Дальнейшие преобразования

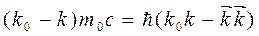
Приводят к выражению интересующей нас величины

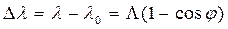(7)

Где и длины волн фотона до и после столкновения, а постоянная величина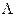

называется комптоновской длиной волны электрона.

В случае рассеяния на другой частице, например, на протоне, в формуле (8) следует заменить массу электрона на массу протона.

Формула (7) точно соответствует результатам эксперимента и получила название комптоновского сдвига (увеличение длины волны рентгеновского кванта после рассеяния).

Как следует из (7), для нулевого угла рассеяния не происходит изменения длины воны (энергии фотона), тогда как для лобового столкновения (для угла рассеяния 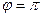) достигается максимальная передача энергии электрону, а рассеянный фотон приобретает минимальную энергию.

(8)

Контрольные вопросы.

1.

Дата добавления: 2015-10-21