Задача2

1. Сколькими способами две пары близнецов можно рассадить на четырех местах?

2. Сколькими способами можно разделить колоду из 36 карт пополам, так, чтобы в каждой части было по 2 туза?

3. Сколькими способами 7 студентов можно поселить в одноместную 2-местную и 4-местную комнаты в общежитии?

4. Сколькими способами 3n предметов можно разложить поровну по n урнам, если

а) урны различны;

б) урны одинаковы?

5. Сколькими способами можно составить ожерелье из 5 бусин синего цвета, 6 бусин красного цвета и 7 бусин зеленого цвета?

6. Имеется n различных предметов и n одинаковых предметов. Сколькими способами можно разложить в ряд 2n предметов.

7. Имеется n различных предметов и n одинаковых предметов. Сколькими способами можно выбрать из них n предметов.

8. Сколькими способами можно поставить белую и черную ладью, так чтобы они не били друг друга.

9. Сколькими способами можно поставить белого и черного слона, так чтобы они не били друг друга?.

10. Сколькими способами можно поставить белого и черного ферзя, так чтобы они не били друг друга?

11. Сколькими способами можно поставить белого и черного короля, так чтобы они не били друг друга?

12. Сколькими способами можно представить число n в виде суммы трех натуральных слагаемых.

13. Сколько можно сделать перестановок из n элементов в которых данные три элемента a, b и c не стоят рядом,

14. Сколько можно сделать перестановок из n элементов в которых никакие два из элементов a, b и c, не стоят рядом.

15. Сколько положительных целочисленных решений имеет система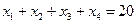

16. В школе 1400 учеников. Из них 1250 умеют кататься на лыжах, 952 - на коньках. Ни на лыжах, ни на коньках не умеют кататься 60 учащихся. Сколько учащихся умеют кататься и на лыжах и на коньках?

17. Сколько чисел из первой тысячи не делится ни на одно из чисел 2, 3, 5?

18. На экзамене были предложены три задачи. Из 1000 абитуриентов первую задачу решили 800, вторую 700, третью 600. Первую и вторую задачу решили 600 абитуриентов, первую и третью -500, вторую и третью - 400, 300 человек решили все задачи. Сколько абитуриентов не решили ни одной задачи.

19. Пусть X={0,1,2,...,100}

P1: x-простое число, ;

P2:; x-четное число, ;

P3: x<70;

20. Сколько существует натуральных чисел меньших миллиона, которые содержат все цифры 1, 2, 3, 4?

21. В отделе НИИ работают X человек. Каждый из них знает хотя бы один иностранный язык. Известно, что английский из них знают 6 человек, немецкий - 6, французский -7, английский и немецкий -4, немецкий и французский -3, французский и английский -2, все три языка -1 человек. Сколько человек работает в отделе?

22. В отделе НИИ работают X человек. Каждый из них знает хотя бы один иностранный язык. Известно, что английский из них знают 6 человек, немецкий - 6, французский -7, английский и немецкий -4, немецкий и французский -3, французский и английский -2, все три языка -1 человек.Сколько из них знают только английский язык?

23. В отделе НИИ работают X человек. Каждый из них знает хотя бы один иностранный язык. Известно, что английский из них знают 6 человек, немецкий - 6, французский -7, английский и немецкий -4, немецкий и французский -3, французский и английский -2, все три языка -1 человек. Сколько из них знают только французский.

24. Подсчитайте количество элементов , не обладающих ни одним из свойств.

Дата добавления: 2015-10-21