Решение типового примера

Решение матричных игр 2х2 в смешанных стратегиях и моделирование результатов

Решение типового примера

Матричную игру 2х2 решить в смешанных стратегиях:

1) аналитически (для игрока А); геометрически (для игрока В)

2) провести моделирование результатов игры с помощью таблицы равномерно распределенных случайных чисел, разыграв 30 партий; определить относительные частоты использования чистых стратегий каждым игроком и средний выигрыш, сравнив результаты с полученными теоретически в п.1.

Игра задана платежной матрицей: .

Решение:

1. Найдем аналитически оптимальную стратегию игрока А и соответствующую цену игры Х*(р₁, р₂), n.

Так как Х* – оптимальная, то она должна гарантировать средний выигрыш игроку А, равный цене игры при любом поведении игрока В:

для стратегии В₁: ;

для стратегии В₂: .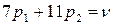

С учетом того, что сумма компонентов смешанной стратегии равна 1, получаем систему уравнений:

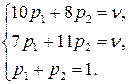
Вычтем из первого уравнения второе: или .Значит:

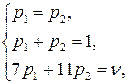
Итак: , n = 9.

Найдем геометрически оптимальную смешанную стратегию игрока В: Y*(q₁, q₂).

Стратегию А₁ изобразим точками с ординатами 10 и 7 на прямых В₁ и В₂ соответственно. Стратегию А₂ – точками с ординатами 8 и 11 (см. рис. 1).

Каждой точке на отрезке [0; 1] соответствует смешанная стратегия игрока В. Среди них оптимальной будет та, которая определяется самой низкой точкой ломанной А₁МА₂, т.е. точкой М. Для нахождения компонентов оптимальной стратегии игрока В надо найти координаты точки М, причем если М (х, у), то q₁ = 1 – х, q₂ = х, n = y. Для этого найдем уравнения прямых А₁А₁ и А₂А₂, воспользовавшись уравнением прямой, проходящей через две точки:

.

Так как А₁(0; 10) и А₁(1; 7), то

, , , .

Т.е. уравнение прямой А₁А₁ имеет вид: .

Рис. 3. Геометрическая интерпретация матричной игры для игрока В

Так как А₂(0; 8) и А₂(1; 11), то

, , , .

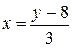Т.е. уравнение прямой А₂А₂ имеет вид: .

Найдем координаты точки М, решив систему уравнений прямых А₁А₁ и А₂А₂:

Итак, , значит n = 9, или .

Ответ: , , n = 9.

2. Проведем моделирование результатов решения с помощью таблицы равномерно распределенных случайных чисел (см. приложение). Для 30 партий хватит 60 чисел, на основе которых будут выбираться стратегии игроками. Используемые случайные числа сгенерированы в MS Excel функцией =СЛЧИС(). В приложении достаточно много чисел, но использовать для моделирования можно любые 60, выбранные произвольно с любого места таблицы. Мы возьмем числа из первого блока (для игрока А используется 1, 3 и 5 столбики).

Будем выбирать стратегии игроков, используя геометрическое определение вероятности. Так как все случайные числа из отрезка [0; 1], то чтобы стратегия А₁ появлялась примерно в половине случаев, будем ее выбирать если случайное число меньше 0,5; в остальных случаях выбирается стратегия А₂. Аналогично для игрока В. Стратегию В₁ будем выбирать, если соответствующее случайное число меньше , в противном случае выбираем стратегию В₁.

Заполним расчетную таблицу:

Номер партии	Случайное число игрока А	Стратегия игрока А (А1: < 0,5)	Случайное число игрока В	Стратегия игрока В (В1: < 0,667)	Выигрыш А	Накоплен­ный выиг­рыш А	Средний выигрыш А (цена игры)
	0,029	А1	0,125	В1			10,000
	0,611	А2	0,490	В1			9,000
	0,766	А2	0,958	В2			9,667
	0,738	А2	0,564	В1			9,250
	0,944	А2	0,257	В1			9,000
	0,416	А1	0,886	В2			8,667
	0,513	А1	0,226	В1			8,857
	0,717	А2	0,467	В1			8,750
	0,994	А2	0,822	В2			9,000
	0,412	А1	0,244	В1			9,100
	0,259	А1	0,176	В1			9,182
	0,610	А2	0,658	В1			9,083
	0,207	А1	0,451	В1			9,154
	0,071	А1	0,994	В2			9,000
	0,391	А1	0,724	В2			8,867
	0,835	А2	0,469	В1			9,000
	0,062	А1	0,392	В1			9,059
	0,181	А1	0,457	В1			9,111
	0,891	А2	0,336	В1			9,053
	0,375	А1	0,094	В1			9,100
	0,009	А1	0,522	В1			9,143
	0,255	А1	0,806	В2			9,045
	0,273	А1	0,562	В1			9,087
	0,111	А1	0,805	В2			9,000
	0,888	А2	0,037	В1			8,960
	0,392	А1	0,341	В1			9,000
	0,843	А2	0,808	В2			9,074
	0,086	А1	0,585	В1			9,107
	0,426	А1	0,370	В1			9,138
	0,562	А2	0,688	В2			9,200

Таким образом, в результате моделирования в 30 партиях цена игры (средний выигрыш) равен 9,2. Этот результат согласуется с теоретической ценой игры 9.

Частоты использования игроками своих чистых стратегий соответственно равны:

Х(18/30;12/30), Y(21/30; 9/30) или

Х(0,6; 0,4), Y(0,7; 0,3)

Сравнивая с теоретическими оптимальными стратегиями Х*(0,5; 0,5) и
Y*(0,67; 0,33) можно сделать вывод, что результаты моделирования достаточно близко им соответствуют даже для небольшого количества партий.

Дата добавления: 2015-10-21