Магнетизм

7. В соленоиде длиной = 1 м с плотной намоткой из провода диаметром d = 1 мм течет ток силой = 10 А. В магнитное поле соленоида влетает под углом 60° к линиям магнитной индукции a-частица (масса т = 6,6×10^{- 27} кг, заряд q = 3,2×10^-19 Кл), ускоренная разностью потенциалов U = 100 В. Найти: радиус и шаг винтовой линии, по которой движется a-частица в магнитном поле; число оборотов, которое она сделает внутри соленоида.

Дано: = 1 м; d = 1 мм = 10^{- 3} м; = 10 А; a = 60°; U = 100 В; т = 6,6×10^{- 27} кг; q = 3,2×10^-19 Кл.

Найти: R, h, N.

Скорость, приобретенная частицей при ускорении электрическим полем с разностью потенциалов U:

.

Внутри соленоида существует однородное магнитное поле с индукцией B = m _0×× m×n× = m ₀× m× / d = 4 p× 10^-7 ×1×10 / 10^-3 = 4 p ×10^-3 Тл. Здесь m ₀ = 4 p× 10^-7 Гн/м – магнитная постоянная, m - магнитная проницаемость среды внутри соленоида (вакуум), n = N_с / = 1/ d - плотность намотки (N_с – число витков соленоида).

На частицу с зарядом q, движущуюся со скоростью в магнитном поле с индукцией В, действует со стороны этого поля сила Лоренца F _л = q× ×B× sin a, где a - угол между векторами .

Под действием этой силы, всегда ортогональной как 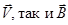, частица в однородном поле движется по винтовой линии, ось которой параллельна линиям индукции . Это движение по винтовой линии может быть представлено как суперпозиция двух более простых движений: а) равномерного движения со скоростью 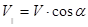вдоль линий магнитной индукции; при этом за время Т одного оборота по винтовой линии частица проходит расстояние h = V _||× T; б) равномерного движения по окружности со скоростью в плоскости, перпендикулярной линиям ; при этом за время одного оборота частица проходит расстояние 2 p × R = V _^× T, где R - радиус окружности (если a = 90 °, частица движется только по окружности - винтовая линия вырождается в окружность).

Применим второй закон Ньютона к движению по окружности:

.

Отсюда находим

м.

Время одного оборота по винтовой линии

с.

Шаг винтовой линии

м.

Число оборотов, сделанное частицей внутри соленоида

8. Напряженность магнитного поля Земли в точке O Н _З = 40 А/м и направлена под углом a = 72,5° к горизонту (рис. 5). Через точки А и В проходят два прямых длинных горизонтальных провода; = 0,2 м. Какие токи и должны течь по этим проводам, чтобы скомпенсировать напряженность магнитного поля Земли в точке O?

Дано: Н _З = 40 А/м; a = 72,5°; = 0,2 м.

Найти:

Согласно принципу суперпозиции для магнитного поля магнитная индукция , создаваемая системой источников магнитного поля, равна векторной сумме магнитных индукций, создаваемых каждым из этих источников. В данном случае

где и - магнитные индукции, создаваемые соответственно первым и вторым проводами с током, - магнитная индукция магнитного поля Земли. Аналогичный принцип суперпозиции справедлив и для напряженности магнитного поля . В рассматриваемом случае необходимо, чтобы результирующая напряженность магнитного поля в точке O равнялась нулю:

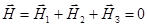. (1)

Введем оси X и Y (рис. 5) и найдем проекции векторов, входящих в равенство (1), на эти оси. Тогда векторное равенство (1) сведется к двум скалярным равенствам:

, (2) . (3)

Рис. 5

Длинный прямой провод с током на расстоянии от него

создает напряженность магнитного поля H = / (2 p× ). Учитывая это в равенствах (2) и (3), получаем систему уравнений:

Из последних уравнений:

При этом ток 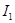должен течь на наблюдателя, а ток 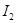- от наблюдателя (рис. 5).

9. Маленькая рамка площадью S = 1 см², имеющая 100 витков, находится на расстоянии r ₀ = 0,5 м от длинного прямого провода с током = 2 А так, что рамка и провод находятся в одной плоскости. Сопротивление рамки R = 0,5 Ом. Провод начинают удалять со скоростью V = 1 м/с от рамки в вышеуказанной плоскости. Определить: ток в рамке, когда провод находится от нее на расстоянии r ₁ = 1 м; заряд, прошедший по цепи рамки при удалении провода на бесконечность. Неоднородностью магнитного поля провода в месте нахождения рамки пренебречь.

Дано: S = 1 см² = 10^-4 м²; N = 100; R = 0,5 Ом; r ₀ = 0,5 м; = 2 А; V = 1 м/с; r ₁ = 1 м.

Найти: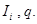

Магнитная индукция, создаваемая длинным прямым проводом с током на расстоянии r от провода,

.

Провод удаляется от рамки со скоростью V, при этом r = r ₀ + V×t и формула для В принимает вид:

.

Потокосцепление рамки

.

При выводе выражения для Y учтено, что магнитная индукция перпендикулярна плоскости рамки.

Согласно закону электромагнитной индукции Фарадея эдс индукции

.

Индукционный ток в рамке найдем из закона Ома

.

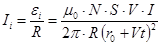Когда провод находится на расстоянии r ₁ от рамки, то r ₀ + Vt = r ₁ и

А.

Заряд, прошедший по цепи рамки, можем найти из соотношения

(1)

В результате получаем

Кл.

Заряд q можно было найти также из соотношения, связывающего заряд с изменением потокосцепления рамки и ее сопротивлением:

,

где Y(r ₀) - потокосцепление рамки на расстоянии r ₀ от провода.

Подставляя сюда выражение для Y(r ₀), получаем

,

т.е. снова приходим к формуле (1).

10. Потокосцепление соленоида длиной = 0,8 м, площадью поперечного сечения S = 250 см², имеющего 800 витков, равно 5×10^{- 3} Вб. Сопротивление соленоида R = 10 Ом. Найти энергию магнитного поля соленоида и ее объемную плотность, а также время, в течение которого напряженность магнитного поля соленоида убывает в 2 раза при отключении источника тока (рис. 6).

Дано: = 0,8 м; S = 250 см² = 2,5×10^-2 м²; N = 800; Y = 5×10^{- 3} Вб; R = 10 Ом; Н ₀ / Н = 2.

Найти:

Индуктивность длинного соленоида L = m₀×m×n ² ×V. Здесь n = N / = 800/0,8 = 10³ м^-1 - число витков, приходящееся на единицу длины соленоида, V = S× = 2,5× 10^-2 × 0,8 = 2 × 10^-2 м³ - объем соленоида.

В результате получаем: L = 4p×10^-7×1×10⁶×2×10^-2 = 2,5×10^-2 Гн.

Ток, текущий по обмотке соленоида

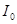= Y/ L = 5×10^{- 3}/ 2,5×10^{- 2} = 0,2 A.

Энергия магнитного поля соленоида

Дж.

Объемная плотность энергии

Дж/м³.

Объемную плотность энергии можно найти также из соотношения, связывающего ее с напряженностью магнитного поля Н ₀:

.

В соленоиде m× = 1, Н ₀ = n× 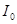= 10³ × 0,2 = 200 А/м.

В результате = 0,5×4 p ×10^-7×1×200² = 2,5×10^-2 Дж/м³.

При выключении источника тока (рис. 6) ток в цепи убывает по закону

,

где R - сопротивление соленоида, L - его индуктивность, 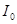- начальное значение тока.

Рис. 6

В соответствии с этим напряженность магнитного поля соленоида также будет меняться по закону

.

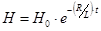Логарифмируя это выражение, получаем ln (H / H ₀) = - (R / L) ×t, что можно переписать в виде ln (H ₀ / H) = (R / L)× t. Время, в течение которого напряженность магнитного поля убывает в 2 раза:

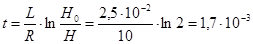с.

ЗАДАЧИ

В таблице приведены номера вариантов и задач. Например, студент, выполняющий вариант 5, должен решить задачи 1, 7, 13, 19, 25, 26, 32, 38, 44,50.

Дата добавления: 2015-10-21