Краткая теория

ИЗМЕРЕНИЕ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ОБРАЗЦОВ С МАЛЫМИ ПАРАМЕТРАМИ РЕЗОНАТОРНЫМ МЕТОДОМ

Методические указания к лабораторной работе

Челябинск 2006

ИЗМЕРЕНИЕ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ОБРАЗЦОВ С МАЛЫМИ ПАРАМЕТРАМИ РЕЗОНАТОРНЫМ МЕТОДОМ.

ЦЕЛЬ РАБОТЫ: экспериментальное определение добротности резонатора с образцом и без образца; нахождение диэлектрической проницаемости образцов малых размеров.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: измеритель КСВН Р2-61, волноводный тракт, прямоугольный резонатор, цилиндрические образцы.

КРАТКАЯ ТЕОРИЯ

Наряду с методами, основанными на измерении полного входного сопротивления с помощью измерительных линий, широкое применение нашли резонаторные методы измерения параметров материалов. В основе резонаторных методов лежит наблюдение резонансных кривых колебательного контура до, и после введения образца материала. В роли непосредственно измеряемых величин в резонаторном методе выступают частоты, добротности и коэффициенты прохождения.

Формулы, связывающие параметры материала с непосредственно измеряемыми величинами, получаются из решений уравнений Максвелла для системы резонатор с образцом материала и энергетических соотношений. Резонаторные методы применимы к измерению параметров материала с относительно малыми потерями.

Рассмотрим прямоугольный резонатор с колебаниями 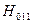(см. рис. 1).

Рис.1. Распределение электрического E и магнитного H полей в прямоугольном резонаторе с модой 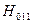(a) и стержень в прямоугольном резонаторе (б) (a=10мм, b=23мм, d=2мм).

В прямоугольной системе координат x, y, z распределение электрического и магнитного полей можно записать в виде

(1)

Резонансная длина волны для колебаний 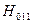может быть найдена по формуле

(2)

Запасённая резонатором энергия рассчитывается через -составляющую

(3)

Рассмотрим случай, когда измеряются параметры цилиндрического образца, расположенного параллельно электрическому полю и ось которого проходит параллельно оси x через точки 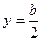, 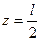. Поле на оси стержня . Находим значение энергии в объёме стержня

, (4)

где d – диаметр стержня.

Добротность резонатора определяется как отношение энергии запасённой в резонаторе к энергии, теряемой за период. Энергия, теряемая за период, рассчитывается по формуле (4).

Кроме того, часто потери в веществе вводят в уравнения, как мнимую часть комплексной диэлектрической проницаемости.

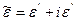, (5)

где - фактическая диэлектрическая проницаемость, - потери.

Известно, что потери и добротность резонатора связаны обратной пропорциональной зависимостью. Отсюда по изменению резонансной частоты и добротности резонатора, после внесения в него исследуемого образца, можно определить и , или и .

Формулы для определения этих величин в простом случае, когда образец малого диаметра расположен в центре резонатора, получаются аналитически. Результат расчётов даёт формулу (6).

, (6)

где - резонансная частота резонатора с образцом; - резонансная частота пустого резонатора; - уход резонансной частоты; - добротность резонатора с образцом; - добротность резонатора без образца.

Таким образом, используя формулу (5), (6) найдем и

(7)

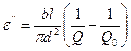(8)

Добротность резонатора определяется по формуле

, при (9)

Рис.2. Резонансная кривая на экране измерителя.

Для определения необходимых величин достаточно, совместить метку последовательно с точками, соответствующими максимуму коэффициента передачи и половине максимального значения коэффициента передачи резонатора, и снять отсчеты частот.

Дата добавления: 2015-10-21