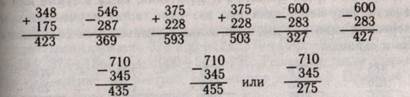Сложение и вычитание в пределах 1000

В изучении действий сложения и вычитания в пределах 1000 можно выделить следующие этапы:

I. Сложение и вычитание без перехода через разряд (устно).

1. Сложение и вычитание круглых сотен.

300-100 500-200

200+100 300+200

Действия производятся на основе знания нумерации и сводятся по существу к действиям в пределах 10. Рассуждения проводятся так:200 — это 2 сотни, 100 — это 1 сотня.

2 сот. + l сот. = 3 сот. 3 сотни — это 300. 200+100=300 500-200=?

5 сот.—2 сот. = 3 сот.=300 500-200 = 300

Отдельным учащимся, которые еще нуждаются в использова-нии средств наглядности, можно предложить пучки палочек (1000 палочек, связанных в пучки по сотне), пластины из арифметичес-

кого ящика, полоски длиной 1 м, разделенные каждая на 100 см, абак, счеты.

Полезно решение и составление троек примеров вида

4+ 2= 7- 5=

40+ 20= 70- 50=

400+200= 700-500=

с последующим сопоставлением компонентов и результатов дейст-

вий.

2. Сложение и вычитание круглых сотен и единиц, круглых
сотен и десятков (действия основываются на знании нумерации):

а) 300+ 5 305- 5 б) 300+ 40 340- 40

5+300 305-300 40+300 340-300

в) 300+ 45 345- 45

45+300 345-300

3. Сложение и вычитание круглых десятков, а также круглых
сотен и десятков:

а) 430+ 20 450- 20 б) 430+200
в) 430+120 550-120 630-200

При решении случаев а), б) рассуждения проводятся так: «430 — это 4 сот. и 3 дес, 20 — это 2 дес. Складываем десятки: 3 дес.+2 дес. = 5 дес. 4 сот.+ 5 дес.=450».

Разряды, которые складываются или вычитаются, можно реко­мендовать подчеркивать:

4 30+ 2 00=630 6 30- 2 00=430

7 Перова М. Н.

При решении примеров вида в) рассуждения проводятся так

«120=100+20, 430+100=530, 530+20=550», т. е. этот случай

сложения (вычитания) сводится к уже известным учащимся слу-чаям сложения (вычитания) а), б).

4. Сложение трехзначных чисел с однозначным, двузначным и
трехзначным без перехода через разряд и соответствующие слу-
чаи вычитания:

а) 540+5 545-5 б) 545+40 в) 350+23 373-23

543+2 545-2 585-40 356+23 379-23

г) 350+123 673-123 356+123 679-123

Выполнение действий производится устно. Учащиеся при выпол-нении действий пользуются теми же приемами, какими они пользо-вались при изучении действий сложения и вычитания в пределах 100, т. е. раскладывают второй компонент действия (второе слагае-мое или вычитаемое) на разрядные единицы и последовательно их складывают или вычитают из первого компонента.

Например:

350+123 ___ 673-123 _______

123=100+20+3 123=100+20+3

350+100=450 673-100=573

450+ 20=470 573- 20=553

470+ 3=473 553- 3=550

5. Особые случаи сложения и вычитания. К ним относятся
случаи, которые вызывают наибольшие трудности и в которых
чаще всего допускаются ошибки. Учащихся больше всего затруд­
няют действия с нулем (нуль находится в середине числа или в
конце). Случай с числами, содержащими нуль, не требует особых
приемов. Но таких примеров надо решать больше, повторить
перед решением таких примеров решение примеров на сложение
и вычитание, когда компонентом действия является нуль: 0+3,
5+0, 5-5:

а) 308+121 б) 402-201 в) 736-504

308+100=408 402-200=202 736-500=236

408+ 20=428 202- 1=201 236- 4=232 428+ 1=429

г) 0+436 700-0 725-725

Устные приемы вычислений требуют от учащихся постоянного анализа чисел по их десятичному составу, понимания места

цифры в числе, понимания того, что действия можно производить

только над одноименными разрядами. Не всем учащимся вспомо-гательной школы это становится понятным одновременно.

Перед выполнением действий необходимо добиваться от уча-

щихся предварительного анализа десятичного состава чисел. Учи-тель чаще должен ставить вопросы: «С чего надо начинать сложе-

ние? Какие разряды складываем?»

В противном случае учащиеся допускают ошибки при вычисле-

ниях. Они складывают десятки с сотнями, а результат записывают

либо в разряд сотен, либо в разряд десятков, например: 400+10=500, 30+400=70, 30+400=4 7 0, 30+400=3 4 0,

670+2=6 9 0, 670-3=6 4 0.

Эти ошибки свидетельствуют о непонимании позиционного зна­чения цифр в числе, о неумении самостоятельно контролировать результаты действий. Учителю необходимо добиваться того, чтобы учащиеся проверяли выполнение действий, причем делали это не формально, а по существу. Нередко приходится наблюдать, что ученик якобы и сделал проверку, но выполнил ее формально. Он записал только обратное действие, а не решал, поэтому и не заметил допущенной ошибки, например: 490—280=110.

Проверка. 110+280=490.

Нередко можно столкнуться с непониманием умственно отста­лыми школьниками (даже старших классов) сущности проверки. Проверка часто выполняется учениками только потому, что этого либо требует учитель, либо такое задание содержится в учебнике. Часто при выполнении проверки ученик получает несоответствие между полученным результатом и заданным примером, но это не служит ему поводом для исправления неверного ответа, например: 570-150=320. Проверка. 320+150=470.

В данном случае проверка выступает как самостоятельное дей­ствие, никак не связанное с тем, которое ученик проверяет.

Учитель постоянно должен помнить об этих ошибках школьни­ков с нарушением интеллекта и требовать ответа на вопросы: «Что показала проверка? Верно ли решен пример? Как доказать, что действие выполнено верно?»

Осознанному выполнению устных вычислений, выработке обоб­щенных способов выполнения действий служит постоянное внима-

7*

ние к вопросам сравнения и сопоставления разных по трудности случаев сложения, вычитания. Важно научить учащихся видеть общее и особенное в тех примерах, которые они решают.

Например, сравнить примеры и объяснить их решение:

30+5, 300+40, 300+45, 300+140, 300+145, 300+105.

305-5, 340-40, 345-45, 340-300, 345-300, 345-200.

Полезно и составление учащимися примеров, аналогичных (по-хожих) данным, или примеров определенного вида: «Составьте пример, в котором надо сложить круглые сотни с единицами»; «Составьте пример на вычитание, в котором уменьшаемое -трехзначное число, а вычитаемое — круглые десятки» и т. д.¹

Для закрепления действий сложения и вычитания в пределах 1000 приемами устных вычислений полезно решение примеров с неизвестными компонентами.

II. Сложение и вычитание с переходом через разряд.

Сложение и вычитание с переходом через разряд — это наибо-лее трудный материал. Поэтому учащиеся выполняют действия в столбик. Сложение и вычитание в столбик производятся над каж-дым разрядом в отдельности и сводятся к сложению и вычитанию в пределах 20. Но в этом случае возникают у умственно отсталых школьников трудности в записи чисел, т. е. в умении правильно подписать разряд под соответствующим разрядом.

Часто из-за неумения организовать внимание, из-за недостаточно четкого понимания позиционного значения цифр в числе, а то и из-за небрежности при записи цифр ученики сдвигают число, которое нужно прибавить или вычесть, влево или вправо и поэтому допуска­ют ошибки в вычислениях. Особенно много ошибок учащиеся допус­кают при записи чисел в столбик, если действие производится над трехзначным и двузначным или однозначным числом. В этом случае десятки подписываются под сотнями, единицы под сотнями или де­сятками. Это приводит к ошибкам в вычислениях.

Например:

375 375 _238

⁺6⁺3818

975 775 58

Наибольшие трудности вызывает действие вычитания. Ошибки в вычислениях носят различный характер. Причиной некоторых из

Слабоуспевающим учащимся разрешается выполнение всех случаев в стол­бик.

них является слабое усвоение табличного сложения и вычитания сделах 20.

238 _275

+ 7 _____ 7

246 266

Много ошибок допускается в результате того, что ученики забывают прибавить получившийся в уме десяток или сотню, а также забывают, что «занимали» сотню или десяток. Например:

178 124

345 '218

292 137

Особенно трудны случаи, при решении которых: 1) переход Через разряд происходит в двух разрядах; 2) получается нуль в одном из разрядов; 3) содержится нуль в уменьшаемом; 4) в середине уменьшаемого стоит единица. Например:

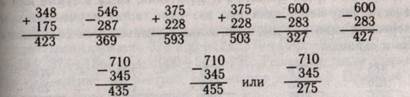
Нередко при вычитании можно встретить и такую ошибку: вместо того чтобы «занять» единицу высшего разряда, раздробить се, ученик начинает вычитать из большей цифры вычитаемого меньшую цифру соответствующего разряда уменьшаемого.

Например:

_375 _529

8 145

«Из 5 единиц 8 единиц 7 десятков и 3 сотни

373 424

При этом рассуждение проводится так: вычесть нельзя, вычитаем из 8 единиц 5, сносим, разность 373».

Сот.	Дес.	Ед.
		6 2

Учитывая трудности изучения данной темы, необходимо повто­рить с учащимися сложение и вычитание с переходом через раз­ряд в пределах 20 и 100, обратить внимание на решение приме­ров, в которых компонентом является нуль, или нуль получается в одном из разрядов суммы или разности (17+3, 25+15, 36—6, 36—27), или нуль содержится в одном из разрядов уменьшаемого или вычитаемого (60—45, 75—40).

Дата добавления: 2015-10-16