Примеры вычисления определённых интегралов.

СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА

ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.

В курсе математического анализа доказано, что неопределённый интеграл функции 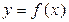по отрезку [a; b] называется определенным интегралом от функции 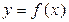по отрезку [a; b] и обозначают так:

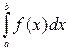
(читают: «интеграл от а до б эф от икс дэ икс»).

Числа а и b называют пределами интегрирования (соответственно нижним и верхним).

Формула Ньютона-Лейбница:

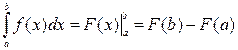
Свойства определённого интеграла:

Правило 1. Интеграл от суммы функций равен сумме интегралов этих функций:

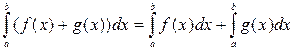
Правило 2. Постоянный множитель можно вынести за знак интеграла:

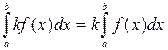
Правило 3. Если 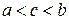, то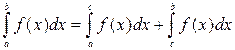

(аддитивное свойство интеграла).

Правило 4.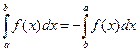

Задание 7: Вычислить:

а) 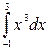б)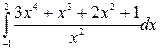

Физический смысл определённого интеграла.

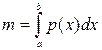, где m – масса неоднородного стержня длиной (b-a) и плотностью р(х)

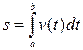, где s – перемещение точки, движущейся по прямой со скоростью 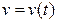за промежуток времени от 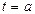до

Геометрический смысл определённого интеграла.

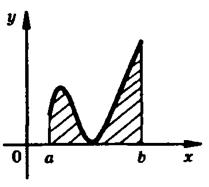
Фигура, ограниченная прямыми 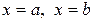, осью Ох и графиком непрерывной и неотрицательной на [а; b] функции 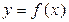, называется криволинейной трапецией.

Площадь криволинейной трапеции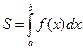

Примеры вычисления определённых интегралов.

1.

2.

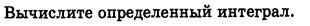
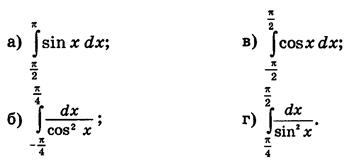
3.

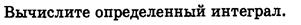
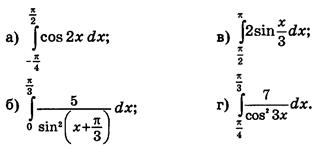
4.

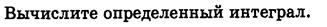
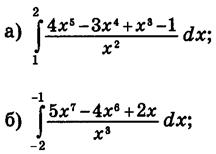
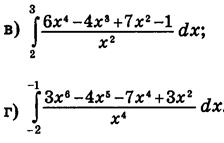
Домашнее задание: подготовка к защите проекта "Применение интеграла"

Ä Математика: учеб. пособие §2.1.12

Ä Заполнить таблицу (Приложение 1)

Индивидуальные задания студентам

Ä из истории интегрального исчисления;

Ä применение интеграла (схема) в математике: (V тела вращения) и физике (S – (путь) перемещения): подготовить теоретический материал+разобрать задачу для примера.

Литература:

Основные источники:

1. Математика: учеб. пособие/В. П. Омельченко, Э. В. Курбатова. - Изд. 7-е, стер. - Ростов н/Д: Феникс, 2013. - 380 с. - (Среднее профессиональное образование).

Дополнительные источники:

1. Богомолов Н. В. Практические занятия по математике: учебное пособие для средних учебных заведений – 7-е издание, М.: Высшая школа, 2004

1. Гмурман В. Е. Теория вероятностей и математическая статистика: учебное пособие – 12-е изд., - М.: Издательство Юраст, 2010

1. Кочетков Е. С. Смергинская С. О., Соколов В. В. Теория вероятностей и математическая статистика – М.: Форум, 2011.

1. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание, стер. – М.: Издательский центр «Академия», 2007

Дата добавления: 2015-10-16