Выбор в условиях риска

1.4

В этом разделе будем предполагать, что с каждой альтернативой А можно связать некоторую репрезентативную случайную характеристику Х_А и функцию распределения этой характеристики F_A. Такой ха­рактер имеют задачи выбора, описанные в этой и последующих гла­вах, до главы 5 включительно: выбор полностью описывается вероят­ностным распределением репрезентативной случайной характеристи­ки. В этом смысле можно говорить о задаче выбора из альтернатив, представленных вероятностными распределениями. Такую задачу на­зывают задачей выбора в условиях риска (choice under risk). В главе 6 рас­сматривается более общая задача выбора в условиях неопределенности (choice under uncertainty).

Так как каждой альтернативе А сопоставляется некоторая ре­презентативная случайная характеристика Х_А с функцией распреде­ления F_a, условимся также писать V(Х_A) и V(F_A), т.е. считать функ­цию V заданной на множестве случайных величин или функций рас­пределения[1]. Такое же соглашение примем и для отношения пред­почтения ≥:.

Детерминированным эквивалентом (certainty equivalent) альтер­нативы А называется число е=е(А), такое, что V(X_A) = V(e). Если, например, альтернативы выбора — некоторые предприятия, дающие случайные доходы Х_А (будем называть такие альтернативы играми или лотереями), то естественно понимать детерминированный эквивалент как цену участия в игре. (См. также упражнение 5.13.)

Зададимся теперь вопросом о том, какими хотелось бы видеть отношение предпочтения и критерии выбора в условиях риска. Есть определенные свойства, которым, по-видимому, должны соответст­вовать любые рациональные предпочтения. Прежде всего, к таким свойствам относится правило "чем больше, тем лучше". Рассмотрим, например, две игры (лотереи). Подбрасывается монета. В первой игре (назовем ее А) можно выиграть 1000 долл. при выпадении герба (с ве­роятностью 1/2) либо не выиграть ничего при выпадении решки. В иг­ре В можно выиграть 1100 долл. при выпадении герба либо ничего в противном случае. Естественно предполагать, что любой рациональ­ный выбор, если есть возможность выбирать между играми А и В, будет в пользу игры В. На рис. 1.2 показаны функции распределения величины выигрыша в играх А и В, F_A(x) и F_B(x).

Можно заметить, что график F_B либо совпадает с графиком F_A, либо лежит ниже его (на интервале от 1000 до 1100). Таково общее правило: смещению рас­пределения вероятностей в область больших значений соответствует понижение графика функции распределения.

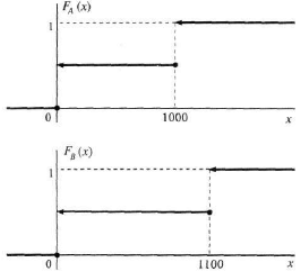
Рис. 1.2. Функции распределения выигрышей в лотереи А и В

Пусть F(x) и G(x) — две несовпадающие функции распреде­ления. Говорят, что функция распределения F(x) доминирует функ­цию распределения G(x) в смысле стохастического доминирования пер­вого порядка (обозначим это F >_IG), если для любого x F(x) ≤ G(x). Для краткости будем употреблять также термин первое стохастиче­ское доминирование.

Можно показать, что если F > _I G, то существуют случайные ве­личины X и Y с функциями распределения F(x) и G(x) соответст­венно, такие, что X ≥ Y, причем при некоторых случайных исходах имеет место строгое неравенство (упражнение 1.6). Это еще одно по­яснение по поводу того, почему стохастическое доминирование пер­вого порядка является аналогом правила "чем больше, тем лучше" для случайных денежных альтернатив.

Разумно потребовать согласованности отношения предпочтения со стохастическим доминированием первого порядка, или, как гово­рят, монотонности относительно первого стохастического доминирова­ния. Сформулируем соответствующее условие на предпочтения.

(М₁) Если F_a>_IF_B, то А > В.

Так называемое неприятие риска (risk aversion) тоже часто рас­сматривается как естественное условие на предпочтения относитель­но рисковых альтернатив. Однако оно не так бесспорно, как правило "чем больше, тем лучше" (М₁). Рассмотрим, например, выбор между игрой А, в которой можно выиграть 1000 долл. с вероятностью 1/2 и ничего с вероятностью 1/2, и игрой В, состоящей в детерминирован­ном получении 500 долл. Заметим, что математические ожидания вы­игрышей равны. Как правило, когда такой выбор предлагают группам людей, большинство отвечает, что они выбрали бы В, однако нахо­дятся и такие, кто предпочел бы А. Если, однако, некто предпочитает Л, можно было бы предложить ему выбор между В и игрой А', в ко­торой можно выиграть 21000 долл. с вероятностью 1/2 и проиграть 20000 долл. в противном случае (математические ожидания выигры­шей по-прежнему равны 500 долл.). Многие, по-видимому, просто откажутся играть в игру А', не говоря уже о том, чтобы предпочесть ее игре В. Во многих ситуациях отказ от риска выглядит рационально, и в реальных экономических ситуациях часто неприятие риска доми­нирует. Например, на фондовом рынке облигации, риск которых оце­нивается рынком как более высокий, имеют и большую доходность: спрос на них ниже и ниже цены, т.е. инвесторы в целом демонстриру­ют неприятие риска.

Сформулируем условие неприятия риска в следующем виде.

Будем говорить, что функция распределения F_A получена из функции распределения F_B сохраняющим среднее рассеиванием (mean preserving spread), если F_A(x) и F_B(x) — две несовпадающие функции распределения, математические ожидания которых равны, т_A=т_B=т, и F_A(x) > F_B(x) для любого х < т, F_A(x) < F_B(x) для любого х > т. (RA) Если функция распределения F_A получена из функции распределе­ния F_B сохраняющим среднее рассеиванием, то F_B> F_A.

Рис. 1.3 и 1.4 иллюстрируют это свойство. Если функции рас­пределения имеют плотности, то они могут выглядеть так, как изоб­раженные на рис. 1.3. Плотность с большей дисперсией (сплошная ли­ния на графике) соответствует функции распределения F_A, получен­ной сохраняющим среднее рассеиванием. Функции распределения, построенные по таким плотностям, показаны на рис. 1.4. Функция F_A имеет больший разброс, давая "более рисковое" распределение, поэто­му, с точки зрения отвергающего риск лица, представляет менее вы­годную альтернативу. На рисунках изображены симметричные плотно­сти и распределения, однако определение применимо к произвольным распределениям.

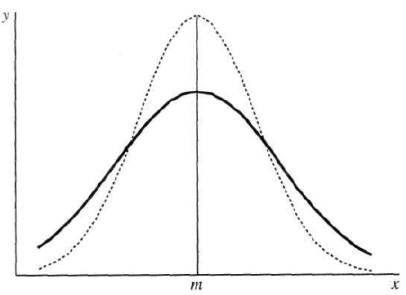
Рис. 1.3. Две нормальные плотности, имеющие одинаковое среднее т и разные дисперсии

Еше одно условие, которое мы введем, объединяет в себе условия стохастического доминирования первого порядка и неприятия риска. Пусть опять F(x) и G(x) — две неодинаковые функции распределе­ния. Будем говорить, что функция распределения F(x) доминирует функцию распределения G(x) в смысле стохастического доминирова­ния второго порядка (обозначим это F >_IIG), если для любого t

Для краткости будем употреблять также термин второе стохастиче­ское доминирование. Введем соответствующее требование монотонности. (М_П) Если F_A>_IIF_A то А > В.

Очевидно, что если F_A>_IF_A, то F_A>_IIF_A. Кроме того, рис. 1.4 показывает, что из двух симметричных распределений с общим центром распределение, имеющее меньший разброс, доминирует другое в смыс­ле второго стохастического доминирования. Действительно, в силу сим­метрии, площадь S₁, тонированной области, лежащей между двумя функциями от - 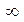до точки их пересечения m, для любого конечно­го t не меньше площади S₂, тонированной области от точки пересе­чения до t. Фигурирующий в определении интеграл равен разности площадей S2- S1, которая, как мы видим, не положительна.

Из всего сказанного следует, что требование (М_II) является бо­лее сильным, чем (М_I) и (RА), т.е. можно написать:

(М_II)=>(М_I); (М_II)=>(RА).

Провести доказательство предоставляется читателю.

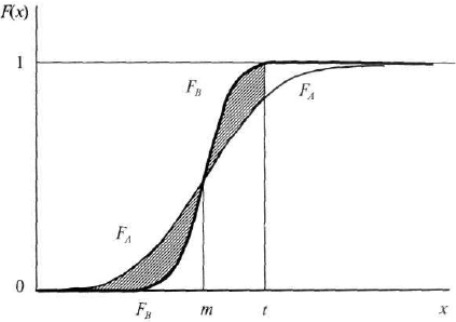
Рис. 1.4. Второе стохастическое доминирование

Нужно заметить, что на рис. 1.3 и 1.4 изображены нормальные плотности и функции распределения. Для нормальных распределе­ний больший разброс определяется большей дисперсией, т.е. если дис­персия одного распределения больше, то оно доминирует другое в смысле второго стохастического доминирования. Однако обычно это не так. При других распределениях большая дисперсия не может га­рантировать наличие стохастического доминирования. Однако верно обратное: если F_A>_IF_B и m_A=m_B, то σ_А≤σ_В, где через т и σ с соответствующими индексами обозначены, как и выше, математиче­ские ожидания и средние квадратические отклонения (упражнение 2.7).

[1] Строго говоря, следует определить три функции, одну на Л, другую на случайных величинах, третью на распределениях. Условимся обозначать все три одной буквой V.

Дата добавления: 2015-10-16