Уравнения по законам Кирхгофа.

Определить ЭДС индукцию в проводнике 10 см, перемещаемся в магнитном поле с индукцией 0,8 Тл перпендикулярно к его линиям, если за время 0,01 с прошел расстояние 10 см.

13) Проводник длиной 25 см с током 10А внесен в магнитное поле перпендикулярно к направлению поля. Под действием электромагнитной силы F он переместился на расстояние b=10 см. Индукция магнитного поля В=1,2 Тл. Определить работу совершенную при перемещении проводника.

Двухобмоточный трансформатор имеет число витков первичной обмотки 220, вторичной 50. Определить коэффициент трансформации и напряжение вторичной обмотки, если первичная обмотка подключена к напряжению 120В.

15) Определить общую емкость батареи конденсаторов и энергию, если С₁ =20мкФ, С₂ =30мкФ, С₃ =20мкФ, С₄ =50мкФ, а напряжение, приложенное U=220В.

16) Для данной цепи известны ЭДС Е1=246 В, Е2=230 В, R1=0,3 Ом, R2=1 Ом, R3=24 Ом. Укажите направление токов и определите их значения контурных токов.

В цепи, изображённой на рисунке 1, рассчитать все токи методом контурных токов. Параметры цепи: Е1 = 24 В, Е2 = 12 В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.

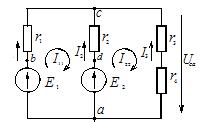
Рис. 1. Схема электрической цепи для примера расчета по методу контурных токов

Решение. Для расчета сложной цепи этим методом достаточно составить два уравнения, по числу независимых контуров. Контурные токи направляем по часовой стрелке и обозначаем I11 и I22 (см. рисунок 1).

По второму закону Кирхгофа относительно контурных токов составляем уравнения:

Решаем систему и получаем контурные токи I11 = I22 = 3 А.

Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. На рисунке 1 такими токами являются I1, I2, I3. Направление у этих токов одинаковое – вертикально вверх.

Переходим от контурных токов к реальным. В первой ветви протекает только один контурный ток I11. Направление его совпадает с направлением реального тока ветви. В таком случае реальный ток I1 + I11 = 3 А.

Реальный ток второй ветви формируется двумя контурными I11 и I22. Ток I22 совпадает по направлению с реальным, а I11 направлен навстречу реальному. В результате I2 = I22 - I11 = 3 - 3 = 0А.

В третьей ветви протекает только контурный ток I22. Направление этого тока противоположно направлению реального, поэтому для I3 можно записать I3 = -I22 = -3А.

Следует отметить, как положительный факт, что в методе контурных токов по сравнению с решением по законам Кихгофаприходится решать систему уравнений меньшего порядка. Однако этот метод не позволяет сразу определять реальные токи ветвей.

17) Для цепи составьте уравнения, используя законы Кирхгофа, если Е₁=24В, Е₂=26В, R₁ =0,3Ом, R₂ =1Ом, R₃ =12Ом. Укажите направление токов в ветвях.

Уравнения по законам Кирхгофа.

1. Изображаем схему цепи в соответствии с исходными данными. Произвольно выбираем и указываем на схеме направления токов в ветвях. Обозначаем узлы схемы. Показываем направления обхода контуров.

2. В схеме имеем шесть неизвестных токов (I₁ - I₆), следовательно, система должна состоять из шести уравнений (К_ур=6).

3. В схеме четыре узла (Кузлов = 4), следовательно по первому закону Кирхгофа необходимо составить три узловых уравнения (К_ур1зак= К_узлов–1=4–1=3) – на одно уравнение меньше, чем количество узлов.

4. Остальные (контурные) уравнения составляются по второму закону Кирхгофа ((Кур2зак = = К_ур – К_ур1зак =6– 3= 3).

5. Согласно первому закону Кирхгофа, алгебраическая сумма токов в узле электрической цепи равна нулю. Знак тока выбираем в зависимости от направления тока – к узлу или от узла.

6. Согласно второму закону Кирхгофа, алгебраическая сумма падений напряжений на сопротивлениях контура равна алгебраической сумме ЭДС этого контура. Знак падения напряжения (тока) и ЭДС определяется в зависимости от его направления по отношению к направлению обхода контура.

7. В соответствии с пунктами 2-6 получаем следующую систему уравнений:

-I₁ + I₂ – I₄ = 0

-I₂ + I₃ – I₅ = 0

I₁ – I₃ + I₆ = 0

-I₁∙R₁– I₂∙R₂ – I₃∙R₃ = Е₁ – E₃

I₂∙R₂ +I₄∙R₄ – I₅∙R₅ = 0

I₃∙R₃ + I₅∙R₅ + I₆∙R₆ = Е₃

18) Определить методом узлового напряжения токи I₁, I₂, I₃ по данной цепи: Е=226В, Е ₂ =230В, R₁ =0,3Ом, R₂ =1Ом, R₃ =22Ом.

Решение:

Находим напряжение между двумя узлами по методу двух узлов

, где

Находим токи по закону Ома

Правильность решения проверим по первому закону Кирхгофа

4,8+5,4-10,2=0

19) Построить векторную диаграмму для цепи, если известны R =43 Ом, Xl =70Ом, Х_с =3Ом, I=0,5А.

Решение:

Находим полное сопротивление цепи, затем полное напряжение и "косинус фи":

2. Строим векторную диаграмму.
Определяем величины напряжений на каждом из элементов цепи.
U(R)=I*R=0.5*43=21.5 (В)
U(С)=I*X(C)=0.5*3=1.5 (B)
U(L)=I*X(L)=0.5*70=35 (B)
По горизонтали откладываем вектор тока I=0.5А. Вектор активной составляющей напряжения U(R) направляем вдоль вектора тока.
Из конца вектора U(R) вертикально вверх откладываем вектор U(L), поскольку сдвиг фазы напряжения на индуктивности составляет +90 градусов. Из конца вектора U(L) вертикально вниз откладываем вектор напряжения на ёмкости U(C), поскольку это напряжение находится в противофазе с индуктивным. Векторная сумма всех трех напряжений дает вектор полного напряжения U.

Дата добавления: 2015-10-16