Задание 2. Звенья W2(s) и W3(s) соединены параллельно; их эквивалентная ПФ соединена последовательно

Задание 1

Расчёт ПФ:

Звенья W2(s) и W3(s) соединены параллельно; их эквивалентная ПФ соединена последовательно со звеном W1(s). Найдём ПФ разомкнутой цепи в общем виде:

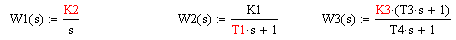
При подстановке числовых значений:

Задание 2

Оцениваем устойчивость системы:

А) корневым методом:

Разомкнутая система:

Один корень нулевой; 2 корня с отрицательной действительной частью; следовательно, разомкнутая система находится на границе устойчивости

Замкнутая система:

Действительная часть всех корней левая; следовательно, замкнутая система устойчива.

Б) Критерием Михайлова

Критерий Михайлова: Система устойчива, если годограф Михайлова начинается на положительной полуоси, и раскручиваясь против часовой стрелки, последовательно проходит n четвертей, где n – порядок характеристического полинома системы.

Разомкнутая система:

Производим замену s→jω:

Выделяем действительную и мнимую составляющую:

Откладывая по оси абсцисс действительную составляющую, а по оси ординат мнимую составляющую, строим годограф Михайлова:

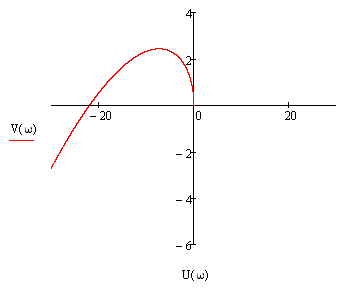
Годограф Михайлова начинается в точке с координатами (0; 0) следовательно, разомкнутая система находится на границе устойчивости.

Замкнутая система:

Производим замену s→jω:

Откладывая по оси абсцисс действительную составляющую, а по оси ординат мнимую составляющую, строим годограф Михайлова:

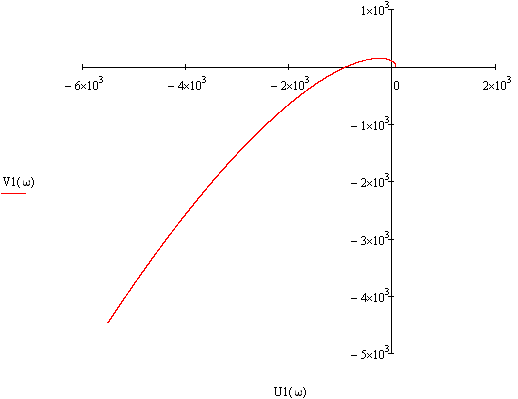
Годограф Михайлова начинается на положительной полуоси и раскручиваясь против часовой стрелки последовательно проходит 3 четверти; следовательно замкнутая система устойчива.

В) Оцениваем устойчивость методами Найквиста

Замкнутая система устойчива, если годограф АФЧХ (Найквиста) разомкнутой системы охватывает точку с координатами (–1; j0) m/2 раз, где m – число правых корней характеристического полинома.

Из п. А мы знаем, что m = 0. Следовательно, замкнутая система будет устойчивой, если годограф АФЧХ не будет охватывать точку с координатами (–1; j0).

Производим замену s→jω:

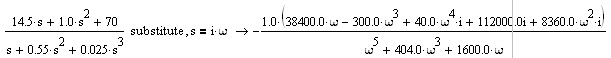
Выделяем действительную и мнимую составляющую:

Откладывая по оси абсцисс действительную составляющую, а по оси ординат мнимую составляющую, строим годограф Найквиста:

Годограф АФЧХ не охватывает точку с координатами (–1; j0), следовательно, замкнутая система будет устойчивой.

Оцениваем устойчивость, используя ЛАЧХ и ФЧХ:

На частоте среза ЛАЧХ значение ФЧХ больше величины –180º, следовательно, замкнутая система будет устойчивой.

Дата добавления: 2015-10-16