Динамика общего объема оборота розничной торговли

Годы	1999	2000	2001	2002	2003	2004
Оборот розничной торговли, млрд. руб. (в фактически действующих ценах)	9,7	0	1,2	-	-	-
Оборот розничной торговли, млрд. руб. (в сопоставимых ценах)	-	-	22,8	4,6	5,2	6,1
Сомкнутый рад абсолютных величин (в сопоставимых ценах; млрд. руб.)	21,3	21,5	22,8	24.6	25,2	26,1
Сопоставимый ряд относительных величин (в % к 2001г.)	92,9	94,3	100	107,9	110,5	114,5

Решение. Чтобы проанализировать динамику общего объема розничной торговли за 1999-2004 гг., необходимо сомкнуть (объединить) приведенные выше два ряда в один. А чтобы уровни нового ряда были сопоставимы, необходимо пересчитать данные 1999-2001 гг. в сопоставимые цены. Для этого на основе данных об объеме розничной торговли за 2001 г. в фактических и сопоставимых ценах находим соотношение между ними: 22,8:21,2 = 1,08. Умножая на полученный коэффициент данные за 1999-2001 гг., приводим их, таким образом, к сопоставимому виду с последующими уровнями. Сомкнутый (сопос­тавимый) ряд динамики показан в предпоследней строке таблицы 9.4.

Другой способ смыкания рядов заключается в том, что уровни года, в котором произошли изменения (в нашем примере - уровни 2001 г.), как до изменений, так и после изменений (для нашего примера - в фактических и сопоставимых ценах, т.е. 21,2 и 22,8) принимаются за 100%, а остальные пересчитываются в процентах по отношению к этим уровням соответственно (в нашем примере в фактических ценах - по отношению к 21,2, в сопоставимых ценах - к 22,8). В результате получаем сомкнутый ряд динамики, который показан в последней строке таблицы 9.4.

Та же проблема приведения к сопоставимому виду возникает и при параллельном анализе развития во времени экономических показателей отдельных стран, администра­тивных и территориальных районов. Это, во-первых, вопрос о сопоставимости цен срав­ниваемых стран, во-вторых, вопрос о сопоставимости методики расчета сравниваемых по­казателей. В таких случаях ряды динамики приводятся к одному основанию, то есть к одному и тому же периоду или моменту времени, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.

Выборочные исследования и наблюдения

Выборочное наблюдение относится к разновидности несплошного наблюдения. Оно охватывает отобранную часть единиц генеральной совокупности. Цель выборочного наблюдения - по отобранной части единиц дать характеристику всей совокупности единиц. Чтобы отобранная часть была репрезентативна (т.е. представляла всю совокупность единиц), выборочное наблюдение должно быть специально организовано. Следовательно, в отличие от генеральной совокупности, представляющей всю совокупность исследуемых единиц, выборочная совокупность представляет ту часть единиц генеральной совокупности, которая является объектом непосредственного наблюдения.

Следует сразу же иметь в виду, что при сопоставлении показателей по результатам выборочного исследования с характеристиками для всей генеральной совокупности могут иметь место отклонения. Величина этих отклонений называется ошибкой наблюдения, которая может быть или ошибкой регистрации (несовершенство технических условий), или ошибкой репрезентативности (случайное или систематическое нарушение правил при отборе единиц).

В статистике приняты следующие условные обозначения:

N - объем генеральной совокупности;

п - объем выборочной совокупности;

- средняя в генеральной совокупности;

- средняя в выборочной совокупности;

р - доля единиц в генеральной совокупности;

w - доля единиц в выборочной совокупности;

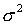- генеральная дисперсия;

S² - выборочная дисперсия;

- среднее квадратическое отклонение признака в генеральной совокупности;

S - среднее квадратическое отклонение признака в выборочной совокупности.

Расчет средней ошибки повторной простой случайной выборки производится следующим образом:

cредняя ошибка для средней

(11.1)

cредняя ошибка для доли

(11.2)

Расчет средней ошибки бесповторной случайной выборки:

средняя ошибка для средней

(11.3)

средняя ошибка для доли

(11.4)

Расчет предельной ошибки повторной случайной выборки:

предельная ошибка для средней

предельная ошибка для доли

(11.5)

где t - коэффициент кратности;

Расчет предельной ошибки бесповторной случайной выборки:

предельная ошибка для средней

(11.6)

предельная ошибка для доли

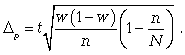(11.7)

Следует обратить внимание на то, что под знаком радикала в формулах при бесповторном отборе появляется множитель, где N - численность генеральной совокупности.

Что касается расчета ошибки выборки в других видах выборочного отбора (например, типической и серийной), то необходимо отметить следующее.

Для типической выборки величина стандартной ошибки зависит от точности определения групповых средних. Так, в формуле предельной ошибки типической выборки учитывается средняя из групповых дисперсий, т.е.

(11.8)

При серийной выборке величина ошибки выборки зависит не от числа исследуемых единиц, а от числа обследованных серий (s) и от величины межгрупповой дисперсии:

(11.9)

Серийная выборка, как правило, проводится как бесповторная, и формула ошибки выборки в этом случае имеет вид

(11.10)

где - межсерийная дисперсия; s - число отобранных серий; S - число серий в генеральной совокупности.

Все вышеприведенные формулы применимы для большой выборки. Кроме большой выборки используются так называемые малые выборки (n < 30), которые могут иметь место в случаях нецелесообразности использования больших выборок.

При расчете ошибок малой выборки необходимо учесть два момента:

1) формула средней ошибки имеет вид

(11.11)

2) при определении доверительных интервалов исследуемого показателя в генеральной совокупности или при нахождении вероятности допуска той или иной ошибки необходимо использовать таблицы вероятности Стьюдента, где Р = S (t, n), при этом Р определяется в зависимости от объема выборки и t.

Простая случайная выборка (собственно-случайная) есть отбор единиц из генеральной совокупности путем случайного отбора, но при условии вероятности выбора любой единицы из генеральной совокупности. Отбор проводится методом жеребьевки или по таблице случайных чисел.

Типическая (стратифицированная) выборка предполагает разделение неоднородной генеральной совокупности на типологические или районированные группы по какому-либо существенному признаку, после чего из каждой группы производится случайный отбор единиц.

Для серийной (гнездовой) выборки характерно то, что генеральная совокупность первоначально разбивается на определенные равновеликие или неравновеликие серии (единицы внутри серий связаны по определенному признаку), из которых путем случайного отбора отбираются серии и затем внутри отобранных серий проводится сплошное наблюдение.

Механическая выборка представляет собой отбор единиц через равные промежутки (по алфавиту, через временные промежутки, по пространственному способу и т.д.). При проведении механического отбора генеральная совокупность разбивается на равные по численности группы, из которых затем отбирается по одной единице.

Комбинированная выборка основана на сочетании нескольких способов выборки.

Задача 4. Методом случайной выборки обследована жирность молока у ста коров. По данным выборки средняя жирность молока – 3,64%. Дисперсия 2,56%. Определить среднюю ошибку выборки при коэффициенте доверия 2 – предельные значения генеральной средней.

Решение:

1. Форма средней ошибки выборки мю = корень из 6 в квадрате: n = корень из 2,56: 100 = 25,6

2. Дельта = t * мю = 25,6 * 2 = 51,2

3. X (генеральная средняя) = X +_ (плюс-минус) дельта = 3,64 +_ 51,2 =

Х1 = 54,84

Х2 = -47,56

4. Предельное значение жирности молока определятся -47,56 меньше или равно х меньше либо равно 54,84. Х = 7%

Задача 5. Для определения средней зарплаты работников была проведена 20% - выборка. Результаты представлены в таблице:

Отдел	Объем выборки (чел)	Средняя зарплата (у.е.)	Среднее квадратическое отклонение (уе)
Итого:		-	-

Определить пределы, в которых находится средняя заработная плата работников при коэффициенте доверия – 3.

Решение:

1. Находим общую выборочную среднюю зарплату

Х = сумма xi * fi: сумму fi = (873 * 120+ 886* 100 + 900*180): 400 = (104760 + 88600 + 162000): 400 = 888,4

2. Находим среднюю из групповых дисперсий

сигма в квадрате (дисперсия) = сумма (сигма в квадрате * f в квадрате): fi = (30 в квадрте (900) * 14400 + 6400 * 10000 + 3600 * 32400): 400 = (12960000 + 64000000 + 116640000): 400 = корень из 48400 = 695,7

3. Определяем предельную ошибку выборочной средней зарплаты для бесповторной выборки:

Дельта = t * корень из ((сигма в квадрате: N) * (1 – (n: N)) = 3 * корень из (484000: 3 * (1 – 0,2 (20%)) = 3* корень из 161333 * 0,8 = 3* корень из 129066 = 1077,8.

N = 400 * 100: 20 = 2000

n – число групп n: N = 20 %

4. Определяем генеральную среднюю:

Х = х +_ дельта = 888,4 +_ 1077,8

Дата добавления: 2015-10-16