Уравнение движения объекта

Целью рассмотрения уравнения движения объекта является определение величины давления в установке, обеспечивающего запуск объекта с определенными МГХ с требуемой скоростью при заданном давлении внешней среды.

Для описания движения объекта при запуске используем второй закон И.Ньютона. Запишем проекцию на продольную ось объекта:

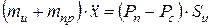, где:

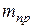- присоединенная масса;

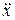- ускорение объекта;

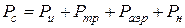- суммарная сила сопротивления, приведенная к эквивалентной величине давления;

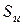- площадь миделя объекта.

Понятие присоединенной массы используется при рассмотрении движения тел в вязкой среде (например: воздух, вода). При движении тела в движение также вовлекается некоторая масса окружающей среды. Причем, различные части среды приобретают различные скорости. Так, можно считать, что элементарные объемы среды, контактирующие с поверхностью тела, имеют скорость, равную скорости тела, а объемы среды, бесконечно удаленные от тела, имеют нулевую скорость. Промежуточные объемы среды осуществляют движение с промежуточными значениями скоростей. Т.о., при приведении в движение тела приходится затрачивать дополнительную энергию на приведение в движение массы окружающей среды. Решение такой задачи о движении среды является очень сложным. Для упрощения вводится понятие присоединенной массы. Присоединенная масса – это такая масса окружающей среды, которая, двигаясь со скоростью тела, имеет кинетическую энергию, равную кинетической энергии масс окружающей среды, движущихся с различными скоростями. Величина присоединенной массы зависит от формы тела, свойств среды и скорости движения тела. Пользуясь тем, что рассматриваемые нами объекты имеют типовую форму и достаточно узкий диапазон скоростей движения при осуществлении запуска, будем определять величину присоединенной массы как 1-5 процентов от массы объекта при движении в воде и ноль – при движении в воздухе.

В рассматриваемом примере (считая, что присоединенная масса составляет 1% от массы объекта) получим значение 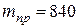кг.

Используя допущение о том, что движение запускаемого объекта до момента выхода из установки равноускоренное, запишем известное выражение для вычисления ускорения:

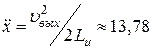м/с².

Теперь рассмотрим силы сопротивления, действующие на объект при запуске. Рассматриваются следующие силы:

· Сила тяжести, приведенная к давлению -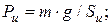

· Сила трения. Используем форму записи через коэффициент трения: 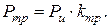В расчетах предлагается брать 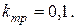Задание силы трения коэффициентом позволяет, при необходимости, учитывать усилие заряжания;

· Силу аэродинамического (при движении в воздухе) или гидродинамического (при движении в воде) сопротивления при проведении предварительного расчета не учитываем, т.е.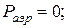

· Сила сопротивления за счет наружного давления среды 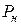берется из исходных данных варианта.

Таким образом, в записанном уравнении движения остается только одна неизвестная величина, которая может быть определена из рассматриваемого уравнения – давление в задонном объеме установки. Для рассматриваемого примера расчета получаем 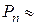7,62·10⁵ Па.

К настоящему моменту получена оценка одного из параметров, характеризующих систему запуска. Это величина давления в установке, обеспечивающая запуск объекта с определенными МГХ с требуемой скоростью при заданном давлении внешней среды.

Дата добавления: 2015-10-21