Областная олимпиада, 1997 г.

1. Пусть – определитель -го порядка с элементами 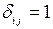при и при 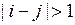. Вычислить .

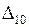2. Написать канонические уравнения прямой , являющейся проекцией прямой на плоскость .

3. Доказать, что .

4. Показать, что функция имеет наибольшее значение и найти его.

5. Найти расстояние от точки до параболы .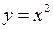

6. Вычислить производную n -го порядка для функции

.

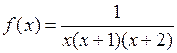7. Вычислить .

8. Найти область определения интегральной экспоненты .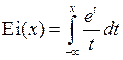

9. Исследовать сходимость ряда .

10. Ряд () сходится. Сходится ли ряд ?

11. Пусть 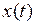решение начальной задачи , , 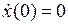. Найти .

12. Найти все ограниченные на промежутке решения дифференциального уравнения .

13. Найти непрерывное решение 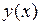, дифференциального уравнения

удовлетворяющее начальному условию , и построить его график.

14. Крестьянка принесла на рынок корзину яблок. Первому покупателю она продала половину всех яблок и еще пол-яблока, второму – половину остатка и еще пол-яблока и т.д. Когда пришел шестой покупатель и купил половину остатка и еще пол-яблока, то оказалось, что у него, как у остальных покупателей, все яблоки целые, а крестьянка продала все яблоки. Сколько яблок было в корзине?

15. Сумма цифр натурального числа равна 1997. Может ли быть это число квадратом другого натурального числа?

Ответы и решения

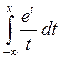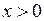8. Пусть . Тогда для . Так как несобственный интеграл , очевидно, сходится, то также сходится. При и потому также сходится. Так как при , а несобственный интеграл расходится, то расходится и несобственный интеграл . Если , то 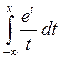также расходится. Итак, несобственный интеграл 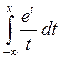сходится при , то есть функция определена на интервале .

Ответ: .

Дата добавления: 2015-10-21