Этапы разработки фильтра

Разработка цифрового фильтра проходит в пять этапов

1. Спецификация требований к фильтру.

2. Вычисление подходящих коэффициентов фильтра.

3. Представление фильтра подходящей структурой.

4. Анализ влияния конечной разрядности на производительность

фильтра.

5. Реализация фильтра на программном и/или аппаратном уровне.

Однако чтобы получить эффективный фильтр, иногда приходится проводить данный процесс в несколько итераций, особенно, если спецификации не являются совершенно определенными (как обычно и бывает), или же разработчик желает исследовать альтернативные структуры.

Спецификация требований включает спецификации:

1) характеристик сигналов;

2) характеристик фильтра;

3) принципа реализации и

4) других требований к структуре (например, стоимость фильтра).

Характеристики цифровых фильтров часто задаются в частотной области. Для частотно-избирательных фильтров, таких как фильтры нижних частот и полосовые фильтры, спецификации часто формулируются в виде схем допусков. Пример подобной схемы для фильтра нижних частот приведен на рис.

9-2. Преобразование Фурье. Преобразование Фурье дельта функции, комплексной экспоненты, константы.

См. вопрос 5-2

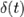
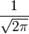
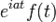
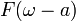
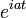
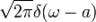
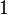
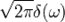
10-1. Основные критерии качества и эффективности цифровых фильтров.

Цифровой фильтр — в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала. В отличие от цифрового аналоговый фильтр имеет дело с аналоговым сигналом, его свойства недискретны, соответственно передаточная функция зависит от внутренних свойств составляющих его элементов.

Разностное уравнение КИХ фильтра.

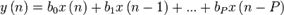
Реализация прямой формы КИХ фильтра:

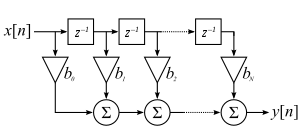
При проектировании цифровых фильтров используются реализационные критерии, определяющие реализационные характеристики, и критерии качества обработки, определяющие характеристики фильтра, влияющие на качество обработки.

Критерий качества обработки определяют требования к основным характеристикам фильтра(АЧХ, ФЧХ, ГВЗ(групповое время задержки), импульсной характеристике), влияющим на качество обработки.

При задании требований к характеристикам фильтра, определяющим качество обработки, часто ограничиваются заданием требований к АЧХ фильтра. Кроме того, дополнительно могут быть заданы требования к иным характеристикам фильтра, влияющим на качество обработки.

В большинстве приложений используются не рекурсивные фильтры с точно линейной ФЧХ.

Точность и качество фильтрации цифрового фильтра зависит от быстродействия АЦП, процессора и ЦАП фильтра, а так же от разрядности АЦП.

Основные характеристики АЧХ фильтров: Частота среда или частоты среза, крутость спада АЧХ с частотой, переходная полоса, пульсации усилений в полосе пропускания и заграждения, порядок фильтра.

Частота дискретизации, используемая в CD дисках - 44,1 кГц, разрядность 16 бит.

Шум квантования — ошибки, возникающие при оцифровке аналогового сигнала. В зависимости от типа аналого-цифрового преобразования могут возникать из-за округления (до определённого разряда) сигнала или усечения (отбрасывания младших разрядов) сигнала. Таким образом на уровень подавляемых помех накладываются ограничения по амплитуде.

10-2. Случайные сигналы и их основные характеристики. Примеры случайных сигналов.

Случайные сигналы — сигналы, мгновенные значения которых (в отличие от детерминированных сигналов) не известны, а могут быть лишь предсказаны с некоторой вероятностью, меньшей единицы. Характеристики таких сигналов являются статистическими, то есть имеют вероятностный вид. Существует 2 основных класса случайных сигналов. Во-первых, это шумы — хаотически изменяющиеся во времени электромагнитные колебания, возникающие в разнообразных физических системах из-за беспорядочного движения носителей заряда. Во-вторых, случайными являются все сигналы, несущие информацию, поэтому для описания закономерностей, присущих осмысленным сообщениям, также прибегают к вероятностным моделям.

Математическое ожидание СВ, распределение которой задаётсяп лотностью fX(x):

.

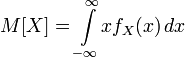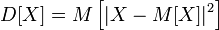
Для эргодической системы среднее по ансамблю совпадает со средним по времени. Для других системы это не всегда выполняется. Для определения параметров системы можно наблюдать за поведением одного её элемента, а можно за очень короткое время рассмотреть достаточно много её элементов. В обоих случаях получатся одинаковые результаты.

Белый шум — стационарный шум, спектральные составляющие которого равномерно распределены по всему диапазону задействованных частот. Примерами белого шума являются шум близкого водопада

Случайный процесс, представляющий собой множество (ансамбль) детерминированных реализаций, не может быть описан комплексной спектральной плотностью, даже и усредненной, так как из-за случайности и независимости фаз составляющих в различных реализациях усреднение приводит к нулевому результату (при mx=0). Однако можно ввести понятие спектральной плотности среднего квадрата случайного сигнала, поскольку средний квадрат не зависит от соотношения фаз суммируемых гармоник.

В обработке сигналов автокорреляционная функция (АКФ) определяется интегралом:

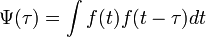и показывает связь сигнала (функции 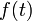) с копией самого себя, смещённого на величину τ.

Теорема Хинчина —утверждает, что спектральной плотностью мощности стационарного в широком смысле случайного процесса является преобразование Фурье соответствующей автокорреляционной функции.

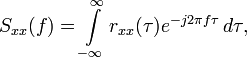
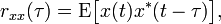
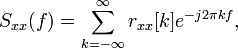
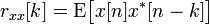
11-1. Дискретное преобразование Фурье. Связь спектральных отсчетов дискретного преобразования Фурье и спектра дискретного и аналогового сигнала.

Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно изпреобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать частные дифференциальные уравнения и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.

Прямое преобразование:

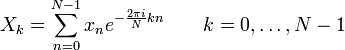
Обратное преобразование:

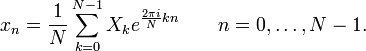
Обозначения:

N — количество значений сигнала, измеренных за период, а также количество компонент разложения;

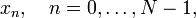— измеренные значения сигнала (в дискретных временных точках с номерами 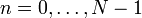, которые являются входными данными для прямого преобразования и выходными для обратного;

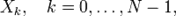— N комплексных амплитуд синусоидальных сигналов, слагающих исходный сигнал; являются выходными данными для прямого преобразования и входными для обратного; поскольку амплитуды комплексные, то по ним можно вычислить одновременно и амплитуду, и фазу;

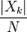— обычная (вещественная) амплитуда k-го синусоидального сигнала;

arg(Xk) — фаза k-го синусоидального сигнала (аргумент комплексного числа);

k — частота k-го сигнала, равная , где T — период времени, в течение которого брались входные данные.

Из последнего видно, что преобразование раскладывает сигнал на синусоидальные составляющие (которые называются гармониками) с частотами от N колебаний за период до одного колебания за период.

Свойства ДПФ.

Свойство 1. Линейность

Свойство 2. Временной сдвиг

Свойство 3. ДПФ циклической свертки сигналов

Свойство 4. Спектр произведения двух сигналов

Свойство 5. Свойство частотного сдвига

Свойство 6. Инверсия спектра действительного сигнала

Связь спектральных отсчетов дискретного преобразования Фурье и спектра дискретного и аналогового сигнала.

Спектральные отсчеты ДПФ являются спектром дискретного сигнала, либо дискретизированного сигнала. А Спектральные отсчеты ДПФ аналогового сигнала, составляют часть спектра аналогового сигнала, взятого с частотой дискретизации.

11-2. Корреляционная и автокорреляционная функции.

Корреляционная функция — функция времени или пространственных координат, которая задает корреляцию в системах со случайными процессами.

Зависящая от времени корреляция двух случайных функций X(t) и Y(t) определяется, как

,

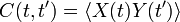где угловые скобки обозначают процедуру усреднения.

Если корреляционная функция вычисляется для одного и того же процесса, она называется автокорреляционной:

.

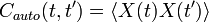Аналогично, можно вычислить корреляционную функцию для процессов, происходящих в разных точках пространства в различные моменты времени:

.

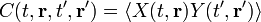Корреляционные функции широко используются в статистической физике и других дисциплинах, изучающих случайные (стохастические) процессы.

Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.

Автокорреляционная функция.

В обработке сигналов автокорреляционная функция (АКФ) определяется интегралом:

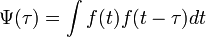
и показывает связь сигнала (функции 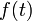) с копией самого себя, смещённого на величину τ.

В теории случайных функций АКФ является корреляционным моментом двух значений одной случайной функции :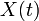

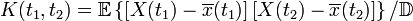
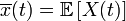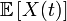Здесь , а — математическое ожидание.

12-1. Спектр дискретного случайного процесса. Методы оценки спектра дискретного случайного процесса..

Для определения спектральных характеристик дискретного случайного процесса вычисляется средний спектр мощности его ограниченного по длине фрагмента, а затем длина фрагмента устремляется к бесконечности:

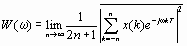
Здесь x(k) — отсчеты случайного процесса, T — период дискретизации. Черта сверху обозначает усреднение по ансамблю реализаций.

Кроме того, этот спектр можно выразить через корреляционную функцию случайного процесса:

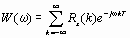
Это выражение представляет собой дискретный аналог теоремы Винера—Хинчина: спектр дискретного случайного процесса является преобразованием Фурье от его корреляционной функции.

12-2. Принципы проектирования БИХ и КИХ фильтров.

Метод рядов Фурье со взвешиванием заключается в начальном математическом определении функции передачи и последующем разложении ее в ряд Фурье. Коэффициенты ряда Фурье определяют импульсную характеристику и, следовательно, коэффициенты КИХ-фильтра.
Затем импульсная характеристика должна быть усечена и подвергнута взвешиванию с использованием оконной функции, как в предыдущем случае. После усечения и применения оконной функции используется БПФ для генерации соответствующей частотной характеристики. Частотная характеристика может быть изменена выбором различных оконных функций, хотя точное управление характеристиками частотной характеристики в полосе режекции затруднено при любом методе, использующем взвешивание с функцией окна.

13-1. Фильтры Бесселя, Баттерворта, Чебышева, Гаусса и Эллиптические.

(Пусть передаточная функция 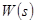, тогда амплитудно-частотная характеристика: 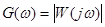, фазо-частотная характеристика: 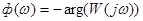, групповая задержка: 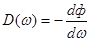.) Фильтр – линейная электрическая цепь, обладающая свойством избирательного пропускания сигналов разных частот. Линейная – в том смысле, что подача на нее синусоидального сигнала не приводит к искажению его формы. Полосовые фильтры пропускают сигналы, лежащие выше определенной нижней, но ниже определенной верхней частоты.

Фильтр Бесселя (относится к БИХ) – один из наиболее распространенных типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика). Передаточная функция: 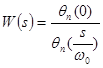, где 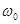- частота среза, 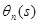- обратный многочлен Бесселя. График АЧХ (красный) и групповой задержки (зеленый):

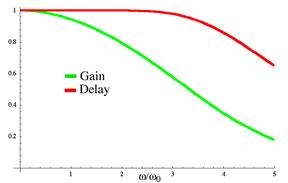
Фильтр Баттерворта (относится к БИХ) – отличается от других методом проектирования – проектируется так, чтобы его амплитудно-частотная характеристика была максимально гладкой на частотах полосы пропускания. Передаточная функция: 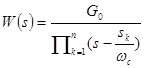, где G₀ – коэффициент усиления по постоянной составляющей (усиление на нулевой частоте), 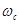- частота среза (частота, на которой амплитуда равна -3дБ), 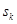-k-ый полюс. АЧХ:

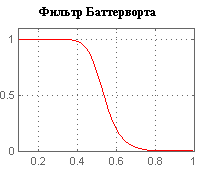
Фильтр Чебышева (относится к БИХ) – один из типов линейных аналоговых или цифровых фильтров, отличительной особенностью которого является более крутой спад АЧХ и существенные пульсации АЧХ на частотах полос пропускания (1 рода) и подавления (2 рода), чем у фильтров других типов. Передаточная функция: 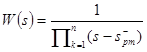, где 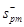- только те полюса, которые имеют отрицательную действительную часть. АЧХ:

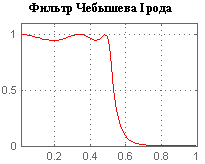
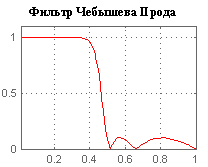
Фильтр Гаусса (относится к КИХ) – электронный фильтр, спроектированный таким образом, чтобы не иметь перерегулирования в переходной функции и максимизировать постоянную времени. Обычно используется в цифровом виде для обработки двумерных сигналов с целью снижения уровня шума.

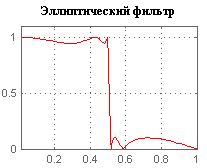
Эллиптический фильтр (фильтр Кауэра) – электронный фильтр, характерной особенностью которого является пульсации АЧХ как в полосе пропускание, так и в полосе подавления. Другой отличительной особенностью является очень крутой спад амплитудной характеристики, поэтому можно достигать более эффективного разделения частот. Если пульсации равны нулю в полосе подавления, то это есть фильтр Чебышева 1 рода, если в полосе пропускания – фильтр Чебышева 2 рода, если пульсаций нет на всей амплитудной характеристике, то это фильтр Баттерворта. АЧХ:

13-2. Проектирование цифровых фильтров в среде LabVIEW и MATLAB.

Для расчета цифровых фильтров в среде MATLAB имеются следующие функции:

BESSELF – проектирование аналогового фильтра Бесселя. BUTTER – проектирование цифрового и аналогового фильтров Баттерворта. CHEBY1 – проектирование цифрового и аналогового фильтров Чебышева 1 рода. CHEBY2 – проектирование цифрового и аналогового фильтров Чебышева 2 рода. ELLIP – проектирование эллиптического цифрового и аналогового фильтров. Выбор порядка фильтра осуществляется с помощью следующий функций:

BUTTORD, CHEB1ORD, CHEB2ORD, ELLIPORD. Но еще лучше проектировать с помощью встроенных в Матлаб средств GUI FDATool, это специальное средство для проектирования фильтров. Обращение из окна Матлаба: fdatool.

Инструментарий проектирования (синтеза) цифровых фильтров (ИПЦФ) в LabVIEW (LabVIEW Digital Filter Design Toolkit) состоит из нескольких рас­ширенных средств для проектирования фильтра, анализа и моделирования циф­ровых фильтров с фиксированной и с плавающей запятой. Процесс проектирования является итерационным. Необходимо эксперимен­тировать с различными техническими требованиями при проектировании или выбирать методы разработки соответствующего цифрового фильтра для прило­жения. Иногда, возможно, потребуется пересмотреть технические требования или изменить метод проектирования после проверки фильтра, особенно при раз­работке фильтров с фиксированной запятой из-за конечной точности коэффици­ентов.

14-1. Дискретное преобразование Фурье. Оценка спектра непрерывного сигнала по его дискретным отсчетам.

Дискретное преобразование Фурье (ДПФ) – один из видов преобразования Фурье, требующее в качестве входа дискретную функцию. Прямое преобразование: 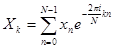, обратное преобразование: 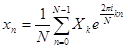, где:

N – количество значений сигнала, измеренных за период, а также количество компонент разложения, xn – измеренные значения сигнала (в дискретных временных точках с номерами n = 0…N-1, которые являются входными данными для прямого преобразования и выходными для обратного), Xk – N-штук комплексных амплитуд синусоидальных сигналов, слагающих исходный сигнал, являются выходными данными для прямого преобразования и входными для обратного. Преобразование раскладывает сигнал на синусоидальные составляющие (которые называются гармониками) с частотами от N колебаний за период до одного колебания за период. Поскольку частота дискретизации сама по себе равна N отсчетов за период, то высокочастотные составляющие не могут быть корректно отображены. Это приводит к тому, что вторая половина из N комплексных амплитуд, фактически, является зеркальным отображением первой и не несет дополнительной информации. ДПФ обладает свойством линейности 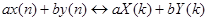, сдвигом по времени 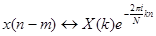, периодичностью 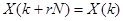, обладает спектральной плотностью .

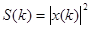14-2. Актуальность цифровых методов обработки для задач телемедицины. GRID-технология на службе здоровья.

Телемедицина – направление медицины, основанное на использовании компьютерных и телекоммуникационных технологий для обмена медицинской информацией между специалистами с целью повышения качества диагностики и лечения конкретных пациентов. Одним из основных направлений телемедицины является дистанционная диагностика – консультации в режиме реального времени. Их проводят с использованием широкополосных каналов связи. Сеанс связи обычно проходит между лечащим врачом и пациентом. В любое время врач посредством сети Интернет и необходимых пакетов программных обеспечений должен получать данные о состоянии здоровья пациентов на любую цифровую систему (комп, ноут, телефон). Поэтому использование цифровых методов обработки особо актуально для телемедицины, которая опирается на эти цифровые методы обработки и хранения медицинских диагностических данных и методы надежной передачи данных по каналам связи.

Грид-вычисления – это форма распределённых вычислений (когда используются несколько компьютеров, объединенных в параллельную вычислительную систему), в которой «виртуальный суперкомпьютер» представлен в виде кластеров, соединённых с помощью сети, слабосвязанных, гетерогенных компьютеров, работающих вместе для выполнения огромного количества заданий. Основным преимуществом распределённых вычислений является то, что отдельная ячейка вычислительной системы может быть приобретена как обычный неспециализированный компьютер. Таким образом, можно получить практически те же вычислительные мощности, что и на обычных суперкомпьютерах, но с гораздо меньшей стоимостью. Типы GRID: Вычислительные GRID - ориентированы на то, чтобы объединять вычислительную мощность для ресурсоемких вычислительных проектов. Информационные GRID - обеспечивают вычислительные ресурсы, для анализа крупномасштабных баз данных коллективного пользования. Коллаборационные GRID - нацелены на работу с большими сложными группами взаимодействующих пользователей (используются, например, для совместного моделирования и проектирования).

15-1. Теорема Котельникова. Условия применимости. Частоты Найквиста и дискретизации.

Теорема Котельникова – любой сигнал с ограниченным спектром можно восстановить без потери информации по своим дискретным отсчетам, взятым с частотой, в 2 раза превышающую максимальную частоту в спектре (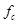). Такая трактовка рассматривает идеальный случай, когда сигнал начался бесконечно давно и никогда не закончится, а также не имеет во временно́й характеристике точек разрыва. Основным условием применимости теоремы является наличие ограниченного частотами среза спектра сигнала. Ограничение спектра сигнала часто выполняется фильтром низких частот. Обычно, реальные сигналы конечны во времени и имеют разрывы во временной характеристике, поэтому их спектр бесконечен, и полное восстановление сигнала невозможно. Тогда говорят о восстановлении с какой-либо точностью. Теорема Котельникова утверждает, что непрерывный сигнал x(t) можно представить в виде интерполяционного ряда: 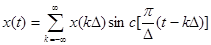, где sinc(x)=sin(x)/x – интегральный синус, интервал дискретизации ограничивается 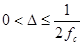, мгновенные значения данного ряда есть дискретные отсчеты сигнала .

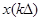Частота дискретизации – частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Частота Найквиста – частота, равная половине частоты дискретизации. Из теоремы Котельникова следует, что при дискретизации аналогового сигнала потерь информации не будет только в том случае, если спектр (спектральная плотность) сигнала равен нулю выше частоты Найквиста. В противном случае при восстановлении аналогового сигнала будет иметь место наложение спектральных «хвостов» (подмена частот, маскировка частот), и форма восстановленного сигнала будет искажена. Если спектр сигнала не имеет составляющих выше частоты Найквиста, то он может быть (теоретически) продискретизирован и затем восстановлен без искажений.

15-2. Импульсная характеристика дискретной линейной системы.

Импульсная характеристика h(k) дискретной системы является откликом системы на единичную функцию x₀(k), являющуюся аналогом дельта-функции при описании дискретных систем и представляющую собой единичный отсчет с единичным значением: 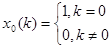. 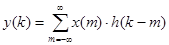- Дискретная линейная свертка входного сигнала и импульсной характеристики. Для того чтобы система была физически реализуема, ее импульсная переходная функция должна удовлетворять условию: h(t)=0 при t<0. В противном случае система нереализуема, так как она нарушала бы причинно-следственную связь: отклик появляется на выходе раньше, чем на вход поступило воздействие. Импульсная характеристика является основной характеристикой линейной системы. Чтобы ее рассчитать, необходимо решить соответствующие разностные уравнения дискретной системы вида 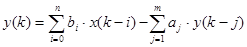, где 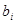, 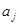- вещественные коэффициенты, называемые внутренними параметрами линейной дискретной системы, 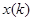, 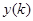- воздействие и реакция. Линейное разностное уравнение является аналогом линейного дифференциального уравнения для аналоговой системы.

16-1. Основные методы обработки изображений, используемые в сканирующей зондовой микроскопии.

Сканирующий зондовый микроскоп (СЗМ) – микроскоп для получения изображения поверхности и ее локальных характеристик. Позволяет получить трехмерное изображение поверхности (топографию) с высоким разрешением. Для регистрации различных эффектов используются разные сенсоры. Обычно, снятое на СЗМ изображение трудно поддается расшифровке из-за искажений, и почти всегда результаты подвергаются математической обработке. В случае СЗМ кадра преобразование Фурье производится над дискретными величинами. Фурье-образ поверхности можно получить по следующим формулам: 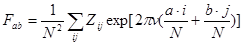, где v – мнимая единица. Обратное преобразование: 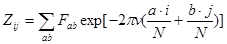. При Фурье-фильтрации производится преобразования над пространственным спектром поверхности. Преобразованный Фурье-образ поверхности запишется в ви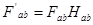де: , где 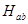- спектральная функция применяемого фильтра. Наиболее распространенными являются фильтры низких и высоких частот с круговыми и квадратными окнами.

16-2. Примеры проектирования КИХ-фильтров и БИХ-фильтров.

КИХ-фильтр – один из видов линейных фильтров с ограниченной по времени импульсной характеристикой. Еще называется не рекурсивным, из-за отсутствия обратной связи. Знаменатель передаточной функции такого фильтра – константа. Разностное уравнение: 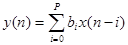, передаточная функция: 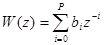. КИХ фильтры могут быть реализованы с использованием умножителей, сумматоров и блока задержки:

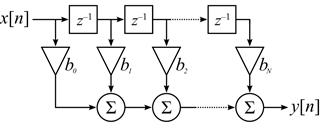
БИХ-фильтр – один из видов линейных фильтров, импульсная характеристика которого имеет бесконечную длину во временной области, а передаточная функция имеет дробно-рациональный вид. Еще называется рекурсивным, потому что использует один или более своих выходов в качестве входа, то есть образует обратную связь. Если рассматривается передаточная функция вида 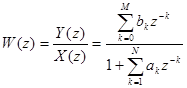, то ей соответствует разностное уравнение: 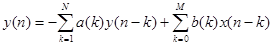. Такая форма построения цепи называется прямой формой:

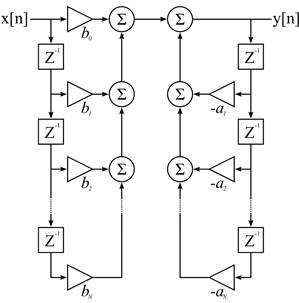
Неканоническая структура, которая подчиняется уравнениям: 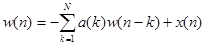и 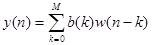. Ее схема:

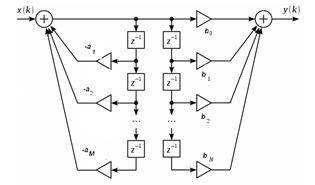
Если объединить задержки, получим каноническую форму:

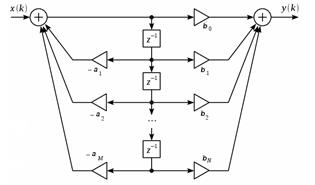
17-1. Прямое и обратное дискретное преобразование Фурье

Прямое преобразование:

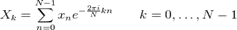
Обратное преобразование:

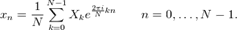
Обозначения:

N — количество значений сигнала, измеренных за период, а также количество компонент разложения;

xn — измеренные значения сигнала (в дискретных временных точках с номерами, которые являются входными данными для прямого преобразования и выходными для обратного;

Xk — ‪N комплексных амплитуд синусоидальных сигналов, слагающих исходный сигнал; являются выходными данными для прямого преобразования и входными для обратного; поскольку амплитуды комплексные, то по ним можно вычислить одновременно и амплитуду, и фазу;

Xk / N - обычная (вещественная) амплитуда k-го синусоидального сигнала;

‪arg(Xk) — фаза k-го синусоидального сигнала (аргумент комплексного числа);

‪k — частота k-го сигнала, равная, где ‪T — период времени, в течение которого брались входные данные.

Из последнего видно, что преобразование раскладывает сигнал на синусоидальные составляющие (которые называются гармониками) с частотами от N колебаний за период до одного колебания за период. Поскольку частота дискретизации сама по себе равна N отсчётов за период, то высокочастотные составляющие не могут быть корректно отображены — возникает муаров эффект. Это приводит к тому, что вторая половина из N комплексных амплитуд, фактически, является зеркальным отображением первой и не несёт дополнительной информации.

Рассмотрим некоторый периодический сигнал ‪x(t) c периодом равным T. Разложим его в ряд Фурье:

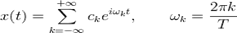
Проведем дискретизацию сигнала так, чтобы на периоде было N отсчетов. Дискретный сигнал представим в виде отсчетов: ‪xn = x(tn), где, 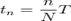тогда эти отсчеты через ряд Фурье запишутся следующим образом: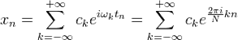

Используя соотношение: 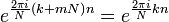, получаем: 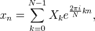где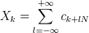

Таким образом мы получили обратное дискретное преобразование Фурье.

Умножим теперь скалярно выражение для ‪xn на 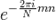и получим:

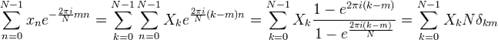
Здесь использованы: а) выражение для суммы конечного числа членов (экспонент) геометрической прогрессии, и б) выражение символа Кронекера как предела отношения функций Эйлера для комплексных чисел. Отсюда следует, что:

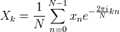
Эта формула описывает прямое дискретное преобразование Фурье.

В литературе принято писать множитель 1/N в обратном преобразовании, и поэтому обычно пишут формулы преобразования в следующем виде: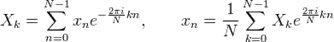

17-2. Роль и место цифровой обработки сигналов в системе наук и ее использование в медицине.

В течение всего 20-го века в медицине и биологии продолжали развиваться методы анализа сигналов и находили применение всѐ большее количество передовых матема- тических методов. Для иллюстрации этого тезиса достаточно назвать только некоторые области исследований в этих направлениях: анализ физиологических сигналов, матема- тические модели физиологических и патологических процессов, поддержка принятия решений (методы искусственного интеллекта), анализ и моделирование макромолекул (фармакология, геномика, протеомика), математическое моделирование лекарственных препаратов, математическое моделирование фармакокинетики лекарств и их метаболи- тов, методы нелинейной динамики для описания физиологических и патологических процессов. Наиболее известными исследованиями на стыке медицины, биологии и ма- тематики в последние десятилетия стали работы по расшифровке генома человека и компьютерному моделированию лекарств.

18-1.Идея быстрого преобразование Фурье. Выигрыш в сравнении с обычным ДПФ.

Быстрое преобразование Фурье (БПФ, FFT) — это алгоритм быстрого вычисления дискретного преобразования Фурье (ДПФ). То есть, алгоритм вычисления за количество действий, меньшее чем ‪O(N2), требуемых для прямого (по формуле) вычисления ДПФ. Иногда под БПФ понимается один из быстрых алгоритмов, называемый алгоритмом прореживания по частоте/времени или алгоритмом по основанию 2, имеющего сложность ‪O(Nlog(N)).

Вывод преобразования из ДПФ

Дискретное преобразование Фурье для вектора 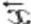, состоящего из N элементов, имеет вид:

элементы матрицы 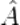имеют вид: .

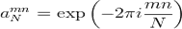Пусть N четно, тогда ДПФ можно переписать следующим образом:

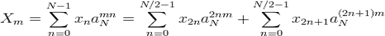
Коэффициенты 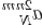и 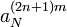можно переписать следующим образом (M=N/2):

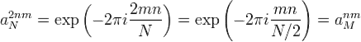
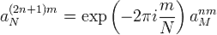
В результате получаем:

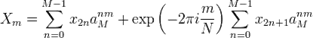
То есть дискретное преобразование Фурье от вектора, состоящего из N отсчетов, свелось к линейной композиции двух ДПФ от N/2 отсчетов, и если для первоначальной задачи требовалось ‪N2 операций, то для полученной композиции — 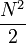. Если M является степенью двух, то это разделение можно продолжать рекурсивно до тех пор, пока не дойдем до двух точечного преобразования Фурье, которое вычисляется по следующим формулам:

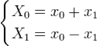
18-2. Основные требования к средствам ЦОС при обработке аудио и видеоинформации.

????????????????????????????????????????????

19-1.Частотные характеристики цифровых фильтров. Свойства частотных характеристик, примеры частотных характеристик.

Цифровой фильтр — в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала. В отличие от цифрового аналоговый фильтр имеет дело с аналоговым сигналом, его свойства недискретны, соответственно передаточная функция зависит от внутренних свойств составляющих его элементов.

Частотная характеристика фильтра представляет собой Фурье-образ его импульсной реакции, и наоборот. При Dt = 1:

H(w) = 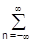h(n) exp(-jwn); h(n) = (1/2p) 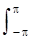H(w) exp(jwn) dw.

В общем случае H(w) является комплексной функцией, модуль которой R(w) называется амплитудно-частотной характеристикой (АЧХ), а аргумент j(w) – фазово-частотной характеристикой (ФЧХ).

A(w) = |H(w)| =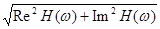

j(w) = arctg(-Im H(w)/Re H(w)).

Основные свойства частотных характеристик цифровых фильтров:

1. Частотные характеристики являются непрерывными функциями частоты.

2. При дискретизации данных по интервалам Dt функция H(w) является периодической. Период функции H(w) равен частоте дискретизации входных данных F = 1/Dt. Первый низкочастотный период (по аргументу w от -p/Dt до p/Dt, по f от -1/2Dt до 1/2Dt) называется главным частотным диапазоном. Граничные частоты главного частотного диапазона соответствуют частоте Найквиста ±wN, wN = p/Dt. Частота Найквиста определяет предельную частоту данных, которую способен обрабатывать фильтр.

3. Для фильтров с вещественными коэффициентами импульсной реакции h(nDt) функция АЧХ является четной, а функция ФЧХ - нечетной. С учетом этого частотные характеристики фильтров обычно задаются только на интервале положительных частот 0-wN главного частотного диапазона. Значения функций на интервале отрицательных частот являются комплексно сопряженными со значениями на интервале положительных частот.

Виды АЧХ для разных шкал:

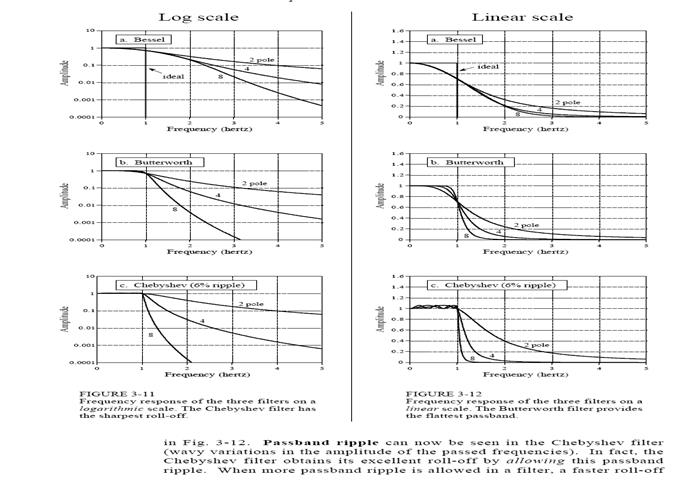
19-2. Необратимость процесса обработки изображений. Теряемая и выявляемая при фильтрации информации.

Суть цифрового преобразования при фильтрации состоит в отсечении вычислительными методами ненужных гармоник. Поступающий на вход каскада сигнал X(N) сдвигается на один такт, умножается на заранее рассчитанный коэффициент C(K), определяющий полосу пропускания фильтра, и затем суммируется с накоплением результата. Применение цифровой обработки в данном случае дает преимущества гибкого изменения полосы пропускания программными методами, технологичности и температурной стабильности, недостигаемой аналоговыми методами.

20-1.Двумерные цифровые сигналы. Двумерное ƒѕ‘, способы его вычисление и примеры использование.

Условимся называть изображением объекта двумерный сигнал, представляющий распределение в картиннои плоскости значений интенсивности (яркости) отраженного от объекта сигнала или интенсивности собственного свечения отдельных элементов объекта.Цифровые данные получаются путем выборки и квантования интенсивности точек из исходных изображений (изображений-оригиналов). Элементы цифрового изображения f (i, j) в i-

м столбце и j-й строке могут быть заданы как бинарные черно-белые (две градации), многоградационные (например, 256 градаций) или в виде многоградационного вектора (например, с 256 градациями по каждой из составляющих — красной, зеленой и синей).

Двумерное преобразование Фурье(n=2)

Преобразование Фурье функций, заданных на пространстве , определяется формулой

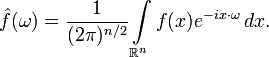
Здесь ‪ω и ‪x — векторы пространства, — их скалярное произведение. Обратное преобразование в этом случае задается формулой

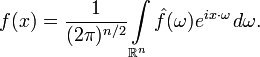
Эта формула может быть интерпретирована как разложение функции ‪f в линейную комбинацию (суперпозицию) «плоских волн» вида с амплитудами, частотами ‪ω и фазовыми сдвигами соответственно. Как и прежде, в разных источниках определения многомерного преобразования Фурье могут отличаться выбором константы перед интегралом.

20-2. Характерные примеры сигналов и спектров, с которыми сталкиваются медики.

??????????????????????????????????????

21-1. Методы описания и анализа дискретных линейных систем.

Линейная система — математическая модель системы, оператор которой обладает свойством линейности.

Учитывая свойство линейности и представление общей последовательности в виде линейной комбинации сдвинутых импульсов,можно заметить, что линейная система полностью определяется своей реакцией на сдвинутые импульсные последовательности. Более того, пусть 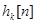- реакция системы на .

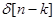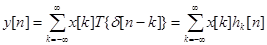
Реакция линейной системы на любую входную последовательность выражается в терминах откликов системы на сигналы 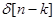. Если система всего лишь линейна, то отсчеты 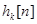зависят как от 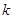так и от 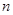, и помощь оказываемая уравнением (выше) при вычислениях, относительно не высока. Существует два основных, тесно связанных между собой, метода анализа линейных систем. Это анализ систем во временной области и анализ систем в частотной области.

Выходной сигнал линейной системы можно представить следующим образом:

.

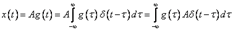Выходной сигнал линейной системы при любом входном воздействии определяется по формуле:

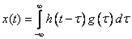
Эта формула называется интегралом Дюамеля или интегралом свертки. Выходной сигнал любой линейной системы получается с помощью взвешивания и последующего интегрирования входного сигнала 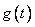с весовой функцией .

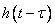21-2. Основные характеристики, области применения и архитектура интегральных схем ЦОС.

Цифровой сигнальный процессор (англ. Digital signal processor, DSP; сигнальный микропроцессор, СМП; процессор цифровых сигналов, ПЦС) — специализированный микропроцессор, предназначенный для цифровой обработки сигналов (обычно в реальном масштабе времени).

Особенности архитектуры

Архитектура сигнальных процессоров, по сравнению с микропроцессорами настольных компьютеров, имеет некоторые особенности:

Гарвардская архитектура (разделение памяти команд и данных), как правило модифицированная;

Большинство сигнальных процессоров имеют встроенную оперативную память, из которой может осуществляться выборка нескольких машинных слов одновременно. Нередко встроено сразу несколько видов оперативной памяти, например, в силу Гарвардской архитектуры бывает отдельная память для инструкций и отдельная — для данных.

Некоторые сигнальные процессоры обладают одним или даже несколькими встроенными постоянными запоминающими устройствами с наиболее употребительными подпрограммами, таблицами и т. п.

Аппаратное ускорение сложных вычислительных инструкций, то есть быстрое выполнение операций, характерных для цифровой обработки сигналов, например, операция «умножение с накоплением» (MAC) (Y:= X + A × B) обычно исполняется за один такт.

«Бесплатные» по времени циклы с заранее известной длиной. Поддержка векторно-конвейерной обработки с помощью генераторов адресных последовательностей.

Детерминированная работа с известными временами выполнения команд, что позволяет выполнять планирование работы в реальном времени.

По сравнению с микроконтроллерами, ограниченный набор периферийных устройств — впрочем, существуют «переходные» чипы, сочетающие в себе свойства DSP и широкую периферию микроконтроллеров.

Области применения

Коммуникационное оборудование:

Уплотнение каналов передачи данных;

Кодирование аудио- и видеопотоков;

Системы гидро- и радиолокации;

Распознавание речи и изображений;

Речевые и музыкальные синтезаторы;

Анализаторы спектра;

Управление технологическими процессами;

Другие области, где необходима быстродействующая обработка сигналов, в том числе в реальном времени.

Дата добавления: 2015-10-16