Астана, 2013

Евразийский национальный университет

Им. Л.Н.Гумилева

Физико-технический факультет

Кафедра «Радиотехника, электроника и телекоммуникации»

Пояснительная записка к курсовой работе по дисциплине «Цифровые устройства и микропроцессоры»

на тему «Проектирование цифрового устройства по заданному алгоритму»

Вариант 2

Выполнил студент гр. РЭТ-34

Амангелдинов Б.

Руководитель

доцент______ Бурамбаева Н.А.

Астана, 2013

СОДЕРЖАНИЕ

ЗАДАНИЕ 1. Минимизация функции с использованием законов алгебры логики………………………………………………………………..………....
ЗАДАНИЕ 2. Минимизация функции с помощью карты Карно…………...
ЗАДАНИЕ 3. Схемная реализация функции с использованием логических элементов в базисе И-НЕ………………………………………..
ЗАДАНИЕ 4. Схемная реализация функции с использованием дешифратора……………………………………………………………….......
ЗАДАНИЕ 5. Схемная реализация функции с использованием мультиплексора………………………………………………………………
ВЫВОД…………………………………………………………………………

ЗАДАНИЕ 1. Минимизация функции с использованием законов алгебры логики.

Булева алгебра позволяет не только математически описывать логические функции, но и преобразовывать их, давая возможность реализовывать эти функции на различных функционально полных системах. Алгебра логики располагает рядом аксиом и законов, основными из которых являются:

1. Аксиомы дизъюнкции

2. Аксиомы конъюнкции

3. Аксиома инверсии

На данных аксиомах базируются также следующие теоремы алгебры логики:

1. Коммутативный закон

2. Ассоциативный закон

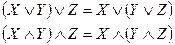
3. Дистрибутивный закон

4. Закон идемпотентности

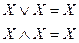
5. Закон поглощения

6. Теорема де Моргана

Минимизируем заданную логическую функцию:

При выполнении минимизации использовались:

1 – теорема де Моргана,

2 – правило раскрытия скобок (дистрибутивный закон),

3 – закон поглощения,

4 – аксиома дизъюнкции,

ЗАДАНИЕ 2. Минимизация функции с помощью карты Карно.

Карта Карно - это графическое представление операций попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно - определенная плоская развертка n-мерного булева куба.

Строится таблица истинности функции определенным образом. Каждая клетка таблицы соответствует вполне определенной вершине булева куба. Нулевые значения не записываются.

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением.

Если функция имеет 6 переменных (в нашем случае), то рисуются 4 карты Карно, так чтобы в соседних картах соседние клетки имели одинаковые координаты.

Минимизируем заданную функцию с помощью карты Карно.

Приведем логическую функцию к виду СДНФ:

Построим карту Карно для 6 переменных и заполним соответствующие ячейки:

В результате минимизации с помощью карты Карно привели функцию к тому же виду, как и в результате минимизации с использованием законов алгебры логики.

ЗАДАНИЕ 3. Схемная реализация функции с использованием логических элементов в базисе И-НЕ.

Микросхема К155ЛА4 представляет собой три логических элемента 3И-НЕ в пластмассовом корпусе 201.14-1 (масса не более 1 г.). Зарубежный аналог микросхемы К155ЛА4 - SN7410. Микросхема КМ155ЛА4 то же самое, что и К155ЛА4, только в металлокерамическом корпусе 201.14-8 (масса не более 2,2 г.).

Предельные параметры микросхемы К155ЛА4

Параметр	Значение
Максимальное напряжение питания	6 В
Максимальное напряжение на выходе закрытой схемы	5,25 В
Входное пробивное напряжение	5,5 В
Минимальное допустимое напряжение на входе схемы	-0,4 В

Электрические параметры микросхемы К155ЛА4

Параметр	Обозначение	Значение
Номинальное напряжение питания	Vcc	5 ± 0,5 В
Время задержки	tзад	9 нс
Максимальное значение тока логического "0" на входе	I0вх	1,6 мА
Максимальное значение тока логической "1" на входе	I1вх	40 мкА
Нагрузочная способность	N
Максимальное значение напряжения логического "0" на выходе	U0вых	0,4 В
Минимальное значение напряжения логической "1" на выходе	U1вых	2,4 В
Максимальное значение тока короткого замыкания	Iкз макс	55 мА
Минимальное значение тока короткого замыкания	Iкз мин	18 мА
Максимальное время задержки включения	t10	15 нс
Максимальное время задержки выключения	t01	22 нс
Максимальное значение входного напряжения, воспринимаемое как уровень логического "0"	U0пор	0,8 В
Минимальное значение входного напряжения, воспринимаемое как уровень логической "1"	U1пор	2 В
Максимальное значение потребляемого тока при логическом "0" на выходе	I0п	16,5 мА
Максимальное значение потребляемого тока при логической "1" на выходе	I1п	6 мА
Максимальная потребляемая статическая мощность на 1 логический элемент	Pлэ	19,7 мВт

ЗАДАНИЕ 4. Схемная реализация функции с использованием дешифратора.

В булевой алгебре широко используется разложение Шеннона — формула, позволяющая перейти к представлению функции n переменных через функции от (n-1) переменных:

Выражение легко обобщается для любого числа переменных, если обе функции его правой части подвергнуть такому же разложению по другим переменным.

Для того чтобы построить схему с использованием дешифратора, выполним разложение Шеннона минимизированной функции по двум переменным:

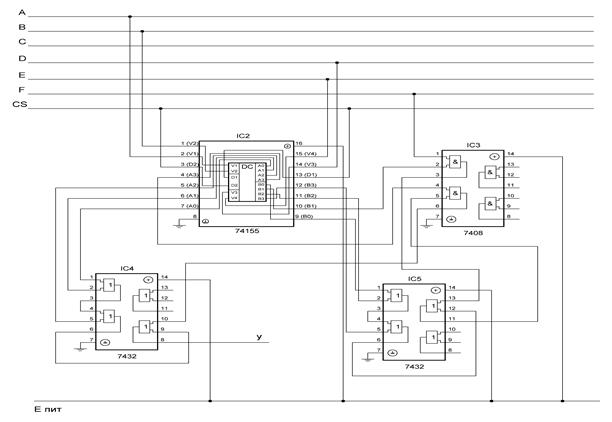
Эксплуатационные параметры используемых элементов:

Два дешифратора на 2 разряда К155ИД4 SN74155

U¹_пор=2,0 В

U⁰_пор=0,8 В

I_п=40 мА

№ кон-такта	I^1вх	I^0вх	N	U^0вых	U^1вых	Iкз(н)	Iкз(в)
мкА	мА	В	В	мА	мА
01, 02, 03, 13, 14, 15		1,6
04, 05, 06, 07, 09, 10, 11, 12				0,4	2,4
	t^10(D)	t^01(D)	t^10(V)^*	t^01(V)^*	t^10(V2)	t^01(V2)
	нс	нс	нс	нс	нс	нс
04, 05, 06, 07, 09, 10, 11, 12

*t_(V) – времена задержек указаны относительно входов V1, V3 и V4

Четыре элемента 2И К155ЛИ1 SN7408

U¹_пор=2,0 В

U⁰_пор=0,8 В

I⁰_п=33 мА

I¹_п=21 мА

№ контакта	I^1вх	I^0вх	N	U^0вых	U^1вых	Iкз(н)	Iкз(в)	t^10	t^01
мкА	мА	В	В	мА	мА	нс	нс
01, 02, 04, 05, 09, 10, 12, 13		1,6
03, 06, 08, 11				0,4	2,4

Четыре элемента 2ИЛИ К155ЛЛ1 SN7432

U¹_пор=2,0 В

U⁰_пор=0,8 В

I⁰_п=38 мА

I¹_п=22 мА

№ контакта	I^1вх	I^0вх	N	U^0вых	U^1вых	Iкз(н)	Iкз(в)	t^10	t^01
мкА	мА	В	В	мА	мА	нс	нс
01, 02, 04, 05, 09, 10, 12, 13		1,6
03, 06, 08, 11				0,4	2,4

ЗАДАНИЕ 5. Схемная реализация функции с использованием мультиплексора.

Для того чтобы построить схему с использованием мультиплексора, выполним разложение Шеннона минимизированной функции по одной переменным:

ВЫВОД

Исходной логической функцией для курсовой работы:

Используя законы и аксиомы алгебры логики, я минимизировала логическую функцию, получила y = .

Затем, произведя минимизацию данной функции с помощью карты Карно, в результате привели функцию к такому же виду.

В данной работе осуществлена схемная реализация одной логической функции различными способами:

1. реализация с использованием логических элементов (в базисе И-НЕ). В схеме использованы 2 микросхемы К155ЛА4 - 3(3И-НЕ)

2. реализация с использованием дешифраторов. В схеме использовано 4 микросхем серии К155: 2 микросхемы К155ИД4 (два дешифратора на 2 разряда), микросхема К155ЛИ1 (четыре элемента 2И), 2 микросхемы К155ЛЛ1 (четыре элемента 2ИЛИ).

3. реализация с использованием мультиплексоров. В схеме использовано 5 мультиплексоров с одним адресным входом.

Дата добавления: 2015-10-21