
Читайте также:
|
Предположим, что вокруг одной из осей гироскопа (рис. 1), например, оси внешней рамки, приложен постоянный внешний момент 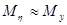 . Будем считать при этом, что моменты по другим осям отсутствуют, а моменты инерции
. Будем считать при этом, что моменты по другим осям отсутствуют, а моменты инерции 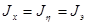 . Принятые допущения соответствуют пренебрежению массой рамок карданова подвеса, т.е. будем рассматривать не гироскоп в подвесе кардана, а так называемый симметричный гироскоп, у которого момент инерции относительно любой экваториальной оси равен
. Принятые допущения соответствуют пренебрежению массой рамок карданова подвеса, т.е. будем рассматривать не гироскоп в подвесе кардана, а так называемый симметричный гироскоп, у которого момент инерции относительно любой экваториальной оси равен 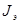 . Однако, как показывает опыт, неучет рамок практически не оказывает влияние на основное (прецессионное) движение гироскопа. Поэтому принятые допущения не нарушат существенно общности основных выводов, но упростят математическую процедуру.
. Однако, как показывает опыт, неучет рамок практически не оказывает влияние на основное (прецессионное) движение гироскопа. Поэтому принятые допущения не нарушат существенно общности основных выводов, но упростят математическую процедуру.
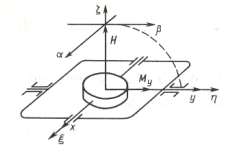
Рис. 1
С учетом принятых ограничений уравнения движения гироскопа запишем в виде:
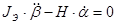
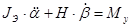 (1)
(1)
Для их решения применим обычный прием снижения порядка уравнений, для чего введем обозначения 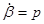 ,
, 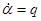 ,
, 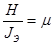 . Тогда уравнения (1) примут вид:
. Тогда уравнения (1) примут вид:
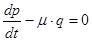
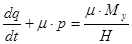 (2)
(2)
Продифференцировав второе уравнение системы (2) и подставив в него значение 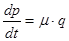 из первого уравнения, получим:
из первого уравнения, получим:
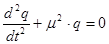
Общее решение такого уравнения, как известно, можно записать так:
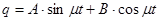 (3)
(3)
где А и В – постоянные интегрирования.
Из второго уравнения системы (2) найдем значение:
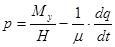 (4)
(4)
Продифференцировав выражение (3) и подставив его в (4), получим решение для второй переменной:
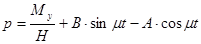 (5)
(5)
Постоянные А и В определим для нулевых начальных условий, т.е. при t = 0, 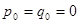 .
.
Тогда из выражений (3) и (5) получим 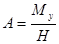 , В = 0, и решения уравнений (2), соответствующие принятым начальным условиям, будут иметь вид:
, В = 0, и решения уравнений (2), соответствующие принятым начальным условиям, будут иметь вид:
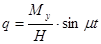
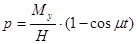 (6)
(6)
Решения (6) выражают закон изменения скоростей 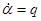 и
и 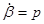 во времени.
во времени.
В программе MathCAD реализовано решение уравнений (2) численным методом Bulirsch-Stoer (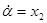 ,
, 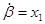 ):
):

|
| Начальные условия |
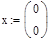
|
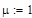
|
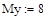
|
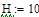
|
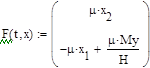
|
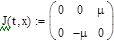
|
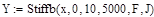
|
Если бы решение поставленной задачи проводились на основании прецессионных уравнений:
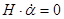
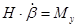 (7)
(7)
то получили бы:
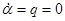
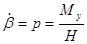 (8)
(8)
Сравнивая решения (6) и (8), полученные на основании решения технических и прецессионных уравнений, заметим, что первые отличаются гармоническими составляющими скоростей 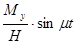 и
и 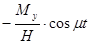 , а вторые являются постоянной составляющей первых.
, а вторые являются постоянной составляющей первых.
Для того, чтобы получить закон изменения углов отклонения главной оси гироскопа, проинтегрируем равенства (6):
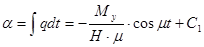
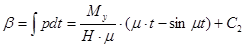 (9)
(9)
Постоянные интегрирования С1 и С2 определим для нулевых начальных условий, т.е. при t = 0, 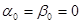 .
.
Тогда из равенств (9) найдем 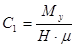 ,
, 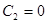 и, окончательно, решения запишем в виде:
и, окончательно, решения запишем в виде:
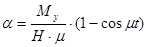
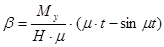 (10)
(10)
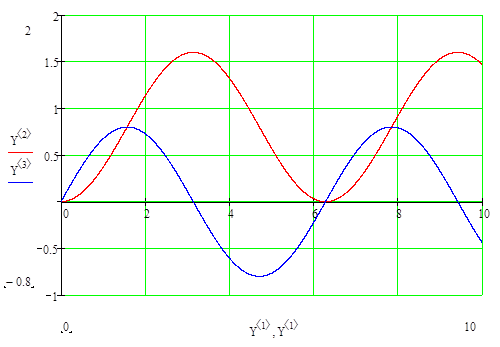
Равенства (10) выражают закон изменения углов 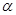 и
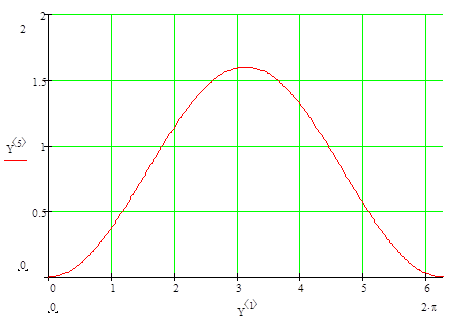
и 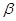 во времени. Построим их графики в среде MathCAD (
во времени. Построим их графики в среде MathCAD (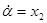 ,
, 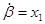 ,
, 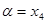 ,
, 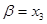 ).
).
| Начальные условия |
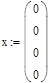
|
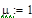
|
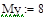
|
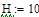
|
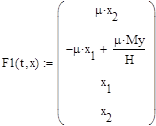
|
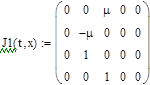
|
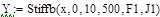
|
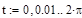
|
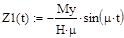
|
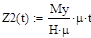
|
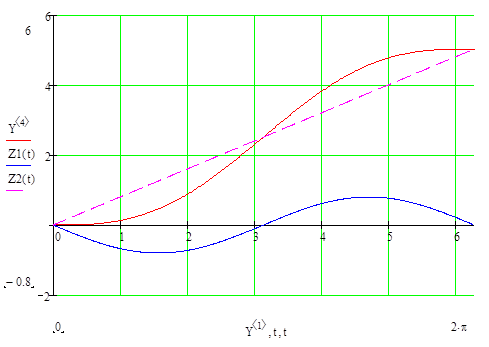
Таким образом, как видно из решения (10), если к гироскопу приложить внешний момент 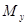 , его главная ось будет совершать сложное движение, состоящее из прецессионного движения вокруг оси х, характеризуемого членом
, его главная ось будет совершать сложное движение, состоящее из прецессионного движения вокруг оси х, характеризуемого членом 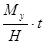 и наложенных на него дополнительных колебаний вокруг осей х и у, характеризуемых соответственно членами
и наложенных на него дополнительных колебаний вокруг осей х и у, характеризуемых соответственно членами 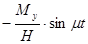 и
и 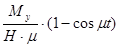 . Это дополнительное движение главной оси гироскопа называют нутационными колебаниями или просто нутацией. Параметрами нутационных колебаний являются их частота
. Это дополнительное движение главной оси гироскопа называют нутационными колебаниями или просто нутацией. Параметрами нутационных колебаний являются их частота 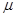 и амплитуды
и амплитуды 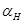 и
и 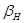 . Для рассмотренного случая
. Для рассмотренного случая 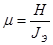 ,
, 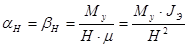 .
.
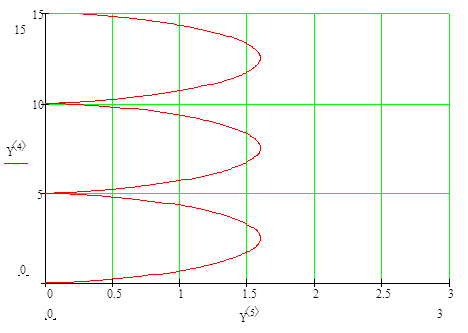
Нетрудно увидеть, что уравнения (10) являются параметрическими уравнениями циклоидами. Следовательно, в координатах 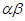 , т.е. на картинной плоскости (при условии малости углов
, т.е. на картинной плоскости (при условии малости углов 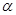 и
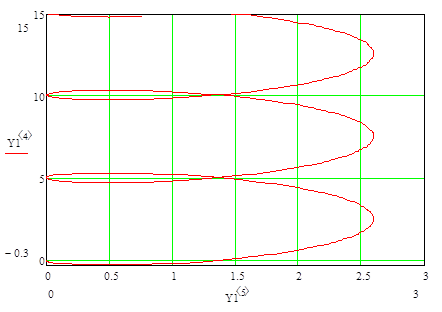
и 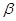 ), вершина гироскопа будет описывать траекторию, являющуюся циклоидой. Такое сложное движение оси гироскопа называют псевдорегулярной (ложно регулярной) прецессией. Так как для подавляющего большинства реальных гироустройств основным движением является прецессионное, а амплитуда и период нутации очень малы, то практически нутационными колебаниями часто пренебрегают. К этому следует добавить, что нутационные колебания быстро затухают благодаря всегда имеющимся в реальных устройствах моментам сил сухого и вязкого трений, которыми при анализе пренебрегли. В общем случае траектория движения вершины гироскопов зависит от начальных условий и может иметь, например, один из следующих видов:
), вершина гироскопа будет описывать траекторию, являющуюся циклоидой. Такое сложное движение оси гироскопа называют псевдорегулярной (ложно регулярной) прецессией. Так как для подавляющего большинства реальных гироустройств основным движением является прецессионное, а амплитуда и период нутации очень малы, то практически нутационными колебаниями часто пренебрегают. К этому следует добавить, что нутационные колебания быстро затухают благодаря всегда имеющимся в реальных устройствах моментам сил сухого и вязкого трений, которыми при анализе пренебрегли. В общем случае траектория движения вершины гироскопов зависит от начальных условий и может иметь, например, один из следующих видов:
- при t = 0, 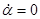 ,
, 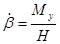
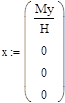
|
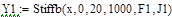
|
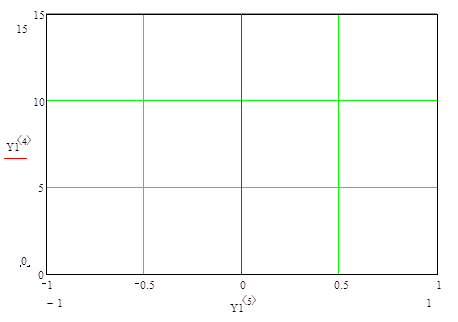
- при t = 0, 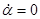 ,
, 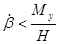
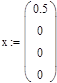
|
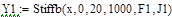
|

- при t = 0, 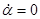 ,
, 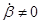 , при этом
, при этом 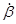 направлена так, что
направлена так, что 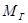 и
и 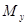 приложены в одном направлении.
приложены в одном направлении.
|
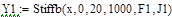
|
Если бы в качестве исходной была взята система уравнений (7), т.е. мы учли бы массу рамок карданова подвеса и приняли 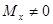 , то качественная картина полученных результатов изменилась бы незначительно. Главная ось гироскопа так же совершила бы псевдорегулярную прецессию в направлении совмещения с вектором момента
, то качественная картина полученных результатов изменилась бы незначительно. Главная ось гироскопа так же совершила бы псевдорегулярную прецессию в направлении совмещения с вектором момента 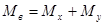 (рис. 2) с частотой нутации
(рис. 2) с частотой нутации 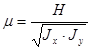 .
.
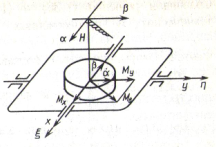
Рис. 2
Амплитуды нутации определялись бы соотношениями 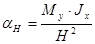 и
и 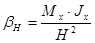 . В общем случае амплитуды нутации зависят и от начальных угловых скоростей
. В общем случае амплитуды нутации зависят и от начальных угловых скоростей 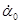 и
и 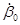 .
.
Если взять начальные условия такими, что в момент времени, соответствующий приложению к гироскопу внешнего момента 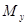 , его главная ось поворачивается (прецессирует) в пространстве вокруг оси х с постоянной угловой скоростью
, его главная ось поворачивается (прецессирует) в пространстве вокруг оси х с постоянной угловой скоростью 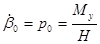 , а вокруг оси у движение отсутствует, т.е. при t = 0,
, а вокруг оси у движение отсутствует, т.е. при t = 0, 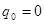 ,
, 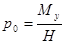 , тогда из выражений (3) и (5) получим А = В = 0 и, следовательно,
, тогда из выражений (3) и (5) получим А = В = 0 и, следовательно, 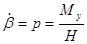 ,
, 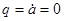 .
.
Это означает, что ось гироскопа сохранит свое начальное состояние, т.е. будет продолжать двигаться (прецессировать) вокруг оси х внутренней рамки со скоростью, соответствующей начальным условиям. Нутационные колебания в данном случае не возникают. Такое движение гироскопа без нутационных колебаний под действием внешнего момента называют регулярной прецессией. Как видно, регулярная прецессия полностью совпадает как по начальным условиям, так и по установившемуся режиму с движением гироскопа.
Таким образом, возникновение нутационных колебаний оси гироскопа обусловлено определенными начальными условиями. Практически они существуют только в переходном процессе, а затем движение вырождается в регулярную прецессию, т.к. нутация – свободные колебания системы, а регулярная прецессия – вынужденное движение. Сравнивая технические и прецессионные уравнения движения гироскопа и их решения, можно сделать вывод, что вторые не учитывают нутационных колебаний гироскопа. Следовательно, причиной возникновения нутации являются «обычные» инерционные члены 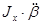 и
и 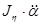 , обусловленные движением гироскопа под действием внешнего момента с угловыми ускорениями
, обусловленные движением гироскопа под действием внешнего момента с угловыми ускорениями 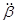 и
и 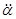 .
.
Дадим физическое пояснение движению оси гироскопа под действием приложенного момента при нулевых начальных условиях (рис. 3). Причиной вызвавшей появление внешнего момента 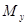 будем считать силу Р, которая может быть обусловлена, например, смещением центра тяжести по оси х на величину
будем считать силу Р, которая может быть обусловлена, например, смещением центра тяжести по оси х на величину 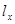 . В начальный момент времени ось z (вектор Н) расположена вертикально и обе рамки карданова подвеса не имеют движения. Постоянный момент
. В начальный момент времени ось z (вектор Н) расположена вертикально и обе рамки карданова подвеса не имеют движения. Постоянный момент 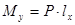 вызовет ускоренное вращение внешней рамки со скоростью
вызовет ускоренное вращение внешней рамки со скоростью 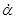 . Эта переносная скорость
. Эта переносная скорость 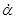 создает гироскопический момент
создает гироскопический момент 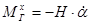 вокруг оси х внутренней рамки, который, в свою очередь, вызовет ускоренное вращение внутренней рамки с угловой скоростью
вокруг оси х внутренней рамки, который, в свою очередь, вызовет ускоренное вращение внутренней рамки с угловой скоростью 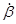 (за положительное направление угла
(за положительное направление угла 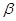 и его производных принята отрицательная часть оси х). Это второе ускоряющееся переносное вращение вызовет второй возрастающий гироскопический момент
и его производных принята отрицательная часть оси х). Это второе ускоряющееся переносное вращение вызовет второй возрастающий гироскопический момент 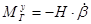 вокруг оси внешней рамки у, направленной против внешнего момента
вокруг оси внешней рамки у, направленной против внешнего момента 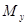 .
.
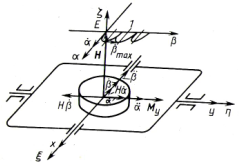
Рис. 3
Пока 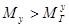 величина
величина 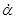 будет возрастать, а вместе с ней будут расти гироскопический момент
будет возрастать, а вместе с ней будут расти гироскопический момент 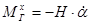 и угловая скорость
и угловая скорость 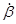 . Когда гироскопический момент
. Когда гироскопический момент 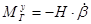 сравняется по величине с
сравняется по величине с 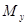 , а затем начнет превышать его,
, а затем начнет превышать его, 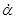 начнет убывать, сохраняя свое направление, а гироскопический момент
начнет убывать, сохраняя свое направление, а гироскопический момент 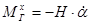 , также уменьшаясь, будет действовать все в том же направлении, а следовательно, будет увеличивать угловую скорость
, также уменьшаясь, будет действовать все в том же направлении, а следовательно, будет увеличивать угловую скорость 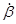 внутренней рамки.
внутренней рамки.
Так как при этом  , то угловая скорость
, то угловая скорость 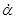 убывает, и когда она станет равной нулю, угловая скорость
убывает, и когда она станет равной нулю, угловая скорость 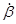 внутренней рамки будет максимальной. Гироскопический момент
внутренней рамки будет максимальной. Гироскопический момент 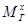 в это мгновение будет равен нулю, а гироскопический момент
в это мгновение будет равен нулю, а гироскопический момент 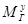 будет максимальным. Затем угловая скорость
будет максимальным. Затем угловая скорость 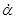 изменит свое направление, и вектор Н под действием разности
изменит свое направление, и вектор Н под действием разности 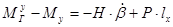 начнет ускоренно поворачиваться в сторону уменьшения угла
начнет ускоренно поворачиваться в сторону уменьшения угла 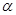 . При этом гироскопический момент
. При этом гироскопический момент 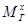 также изменит свое направление (знак) и будет теперь замедлять движение внутренней рамки, т.е. скорость
также изменит свое направление (знак) и будет теперь замедлять движение внутренней рамки, т.е. скорость 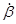 начнет уменьшаться, а следовательно, будет уменьшаться и
начнет уменьшаться, а следовательно, будет уменьшаться и 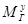 . Пока
. Пока  , скорость -
, скорость - 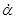 возрастает, и поэтому возрастает гироскопический момент
возрастает, и поэтому возрастает гироскопический момент 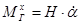 , тормозящий движение внутренней рамки, и угловая скорость
, тормозящий движение внутренней рамки, и угловая скорость 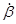 уменьшается. Когда уменьшающийся гироскопический момент
уменьшается. Когда уменьшающийся гироскопический момент 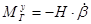 станет опять меньше
станет опять меньше 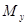 , то движение внутренней и внешней рамок начнет замедляться до тех пор, пока обе скорости -
, то движение внутренней и внешней рамок начнет замедляться до тех пор, пока обе скорости - 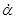 и
и 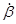 не обратятся в нуль.
не обратятся в нуль.
С этого момента все явления начнут повторяться в той же последовательности. В результате вершина гироскопа (точка Е) будет описывать траекторию, являющуюся правильной циклоидой.
Список использованной литературы
Дата добавления: 2015-10-21; просмотров: 127 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Силовые классы | | | Пояснительная записка |